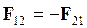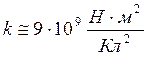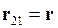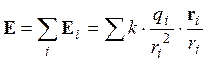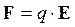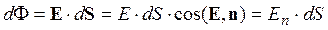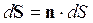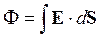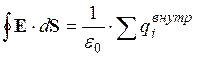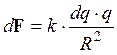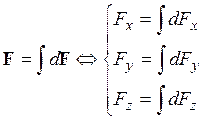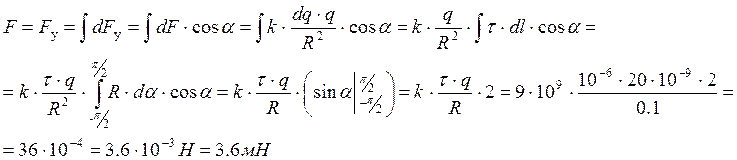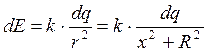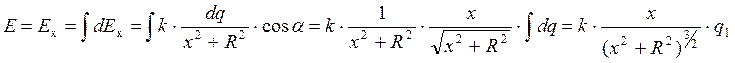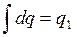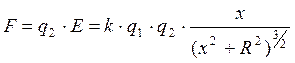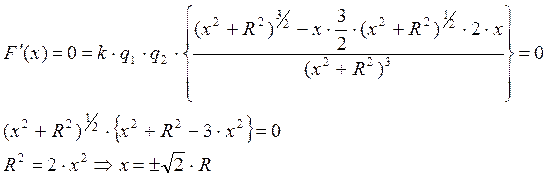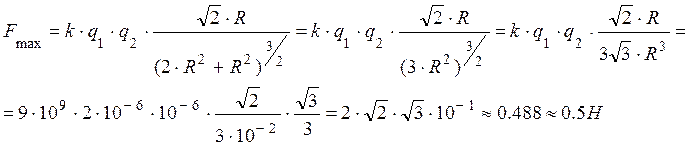равномерно заряженная нить линейной плотностью
С какой силой (на единицу длины) взаимодействуют две бесконечно длинные параллельные равномерно заряженные нити с линейными плотностями зарядов τ1 = 1 мкКл/м и τ2 = 2 мкКл/м, находящиеся в среде с диэлектрической проницаемостью ε = 2 на расстоянии r = 10 см друг от друга. Какую работу (на единицу длины нити) надо совершить, чтобы раздвинуть эти нити дополнительно на расстояние Δd = 5 см.
С какой силой (на единицу длины) взаимодействуют две бесконечно длинные параллельные равномерно заряженные нити с линейными плотностями зарядов τ1 = 2 мкКл/м и τ2 = 1,5 мкКл/м, находящиеся в среде с диэлектрической проницаемостью ε = 3 на расстоянии r = 20 см друг от друга. Какую работу (на единицу длины нити) надо совершить, чтобы раздвинуть эти нити дополнительно на расстояние Δd = 10 см.
С какой силой (на единицу длины) взаимодействуют две бесконечно длинные параллельные равномерно заряженные нити с линейными плотностями зарядов τ1 = 2,5 мкКл/м и τ2 = 1 мкКл/м, находящиеся в среде с диэлектрической проницаемостью ε = 1 на расстоянии r = 30 см друг от друга. Какую работу (на единицу длины нити) надо совершить, чтобы раздвинуть эти нити дополнительно на расстояние Δd = 15 см.
С какой силой (на единицу длины) взаимодействуют две бесконечно длинные параллельные равномерно заряженные нити с линейными плотностями зарядов τ1 = 3 мкКл/м и τ2 = 0,5 мкКл/м, находящиеся в среде с диэлектрической проницаемостью ε = 7 на расстоянии r = 15 см друг от друга. Какую работу (на единицу длины нити) надо совершить, чтобы раздвинуть эти нити дополнительно на расстояние Δd = 7,5 см.
С какой силой (на единицу длины) взаимодействуют две бесконечно длинные параллельные равномерно заряженные нити с линейными плотностями зарядов τ1 = 1,5 мкКл/м и τ2 = 1,5 мкКл/м, находящиеся в среде с диэлектрической проницаемостью ε = 6 на расстоянии r = 10 см друг от друга. Какую работу (на единицу длины нити) надо совершить, чтобы раздвинуть эти нити дополнительно на расстояние Δd = 5 см.
С какой силой (на единицу длины) взаимодействуют две бесконечно длинные параллельные равномерно заряженные нити с линейными плотностями зарядов τ1 = 0,5 мкКл/м и τ2 = 2,5 мкКл/м, находящиеся в среде с диэлектрической проницаемостью ε = 3 на расстоянии r = 20 см друг от друга. Какую работу (на единицу длины нити) надо совершить, чтобы раздвинуть эти нити дополнительно на расстояние Δd = 10 см.
С какой силой (на единицу длины) взаимодействуют две бесконечно длинные параллельные равномерно заряженные нити с линейными плотностями зарядов τ1 = 0,8 мкКл/м и τ2 = 1,0 мкКл/м, находящиеся в среде с диэлектрической проницаемостью ε = 2 на расстоянии r = 10 см друг от друга. Какую работу (на единицу длины нити) надо совершить, чтобы раздвинуть эти нити дополнительно на расстояние Δd = 16 см.
С какой силой (на единицу длины) взаимодействуют две бесконечно длинные параллельные равномерно заряженные нити с линейными плотностями зарядов τ1 = 0,8 мкКл/м и τ2 = 1,0 мкКл/м, находящиеся в среде с диэлектрической проницаемостью ε = 1 на расстоянии r = 10 см друг от друга. Какую работу (на единицу длины нити) надо совершить, чтобы раздвинуть эти нити дополнительно на расстояние Δd = 16 см.
С какой силой (на единицу длины) взаимодействуют две бесконечно длинные параллельные равномерно заряженные нити с линейными плотностями зарядов τ1 = 2,0 мкКл/м и τ2 = 1,6 мкКл/м, находящиеся в среде с диэлектрической проницаемостью ε = 7 на расстоянии r = 30 см друг от друга. Какую работу (на единицу длины нити) надо совершить, чтобы раздвинуть эти нити дополнительно на расстояние Δd = 10 см.
С какой силой (на единицу длины) взаимодействуют две бесконечно длинные параллельные равномерно заряженные нити с линейными плотностями зарядов τ1 = 2,5 мкКл/м и τ2 = 0,6 мкКл/м, находящиеся в среде с диэлектрической проницаемостью ε = 6 на расстоянии r = 20 см друг от друга. Какую работу (на единицу длины нити) надо совершить, чтобы раздвинуть эти нити дополнительно на расстояние Δd = 4 см.
Точечный заряд q = 10 нКл находится в поле, созданном прямой бесконечной нитью, равномерно заряженной с линейной плотностью τ = 0,2 нКл/см. Определить силу F, действующую на заряд, если его расстояние от нити r = 10 см.
Вычислить силу действующую на точечный заряд 0,1 мкКл, расположенный на расстоянии 0,01 м, от бесконечной равномерно заряженной нити с линейной плотностью 2 мкКл/м.
Бесконечная равномерно заряженная нить с линейной плотностью заряда 5·10 –8 Кл/см расположена горизонтально. Под ней на расстоянии 3 см находится в равновесии шарик массой 0,01 г. 1) Определить заряд шарика. 2) Какую работу нужно совершить, чтобы переместить шарик на расстояние 6 см от нити?
Бесконечная равномерно заряженная нить с линейной плотностью заряда 3·10 –8 Кл/см расположена горизонтально. Под ней на расстоянии 2 см находится в равновесии шарик массой 0,01 г. 1) Определить заряд шарика. 2) Какую работу нужно совершить, чтобы переместить шарик на расстояние 4 см от нити?
Система состоит из тонкого проволочного кольца и полубесконечной нити. Конец нити совпадает с центром кольца. Радиус кольца R. Кольцо заряжено зарядом q, а нить заряжена равномерно с линейной плотностью λ. Найти силу их взаимодействия.
Две длинные прямые параллельные нити, заряженные равномерно с линейной плотностью λ, находятся на расстоянии d друг от друга. Найти напряженность поля в точке, лежащей на расстоянии d от обеих нитей.
Бесконечная прямая нить равномерно заряжена с линейной плотностью заряда λ. Найти работу сил поля по перемещению точечного заряда q из точки, находящейся на расстоянии R от нити в точку, находящуюся на расстоянии 2R.
Видео:7 класс, 29 урок, Теоремы об углах, образованных двумя параллельными прямыми и секущейСкачать

Закон Кулона. Принцип суперпозиции. Теорема Гаусса. Потенциал. Проводник в электростатическом поле
Страницы работы
Содержание работы
Видео:6 .7 кл Построение параллельных прямых.Как построить параллельные прямыеСкачать

Урок №1
Закон Кулона. Принцип суперпозиции. Теорема Гаусса.
Одно из фундаментальных взаимодействий – взаимодействие между электрическими зарядами.
Свойства электрического заряда:
1. Существует в двух видах: положительный и отрицательный.
2. В электрически изолированной системе суммарный заряд сохраняется.
3. Величина заряда инвариантна по отношению к инерциальным системам отсчета.
4. Величина заряда диэлектрика: q = N . e, N– целое число, e = — 1.6 . 10 -19 Кл.
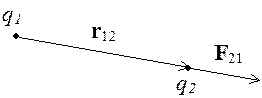
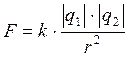
Сила направлена по прямой, соединяющей заряды, и является силой отталкивания, если заряды одноименные, и силой притяжения, если заряды разного знака.
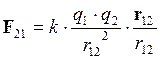
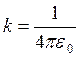
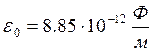
Законом Кулона можно воспользоваться и в том случае, если один из зарядов или оба заряда не являются точечными, но их распределение обладает сферической симметрией. В этом случае r – расстояние между центрами зарядов.
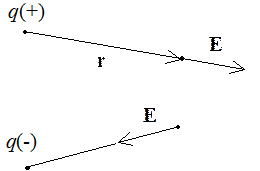
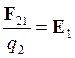
Отвлекаясь от индексов 1 и 2, 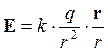
Таким образом, напряженность поля в некоторой точке – это сила, действующая на единичный положительный заряд, помещенный в данную точку поля.
Принцип суперпозиции: напряженность электрического поля в данной точке определяется векторной суммой напряженностей полей, создаваемых отдельными зарядами в этой точке.
Если заряды распределены непрерывно, то
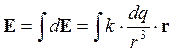
dq = s . dl, s – поверхностная плотность заряда, или
dq = r . dV, r – объемная плотность заряда.
Силу, действующую на произвольный заряд q, помещенный в точку поля, где напряженность Е, можно найти по формуле:
Потоком вектора Е через площадку dS называется:
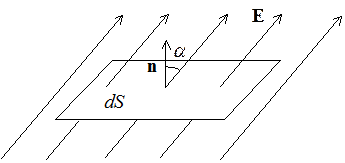
где n – единичный вектор нормали к данной площадке. Если площадка замкнутая, то в качестве положительной нормали всегда выбирается внешняя.
Поток вектора Е через произвольную площадку S определяется:
Оказывается, что поток вектора Е через замкнутую поверхность равен алгебраической сумме зарядов, охватываемых этой поверхностью, деленной на e0:
Данное утверждение называют теоремой Гаусса.
Теорема Гаусса в дифференциальном виде:
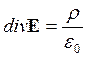
r – объемная плотность электрического заряда в той точке, где ищется 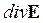
Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Примеры решения задач
Задача №1
Тонкое полукольцо радиусом 10 см равномерно заряжено с линейной плотностью заряда 1 мкКл/м. В центре кривизны полукольца находится точечный заряд 20 нКл. Найти силу взаимодействия точечного заряда и полукольца.
Поскольку заряженное полукольцо не является точечным зарядом, то его следует мысленно разбить на элементарные заряды dq = t . dl, где элемент дуги 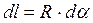

Результирующая сила F найдется векторной суммой всех dF, действующих на заряд q:
Из симметрии задачи можно понять, что результирующая сила F направлена вертикально вниз. Выберем в этом направлении ось y, тогда для величины силы F:
Задача №2
По тонкому кольцу радиуса 10 см равномерно распределен заряд 2 мкКл. Найти максимальную силу, действующую на точечный заряд 1 мкКл, находящийся на оси кольца.
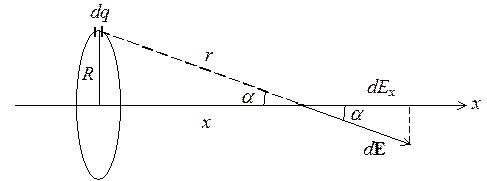
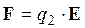
Вычислим 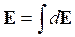
Из симметрии задачи следует, что результирующий вектор E будет направлен по оси х, поэтому
Суммирование всех элементарных зарядов по кольцу даст нам суммарный заряд кольца:
Чтобы найти максимальную силу, нужно определить расстояние х (от центра кольца до точки расположения заряда q2), при котором функция F(x) имеет максимум:
В двух точках на оси, расположенных слева и справа от плоскости кольца на расстоянии 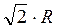
Задача №3
Две длинные прямые параллельные нити, заряженные равномерно с линейной плотностью 20 нКл/м, находятся на расстоянии 10 см. Найти напряженность поля в точке, лежащей на расстоянии 10 см от обеих нитей.
Поле E найдем по принципу суперпозиции, как сумму полей двух нитей: 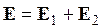
Видео:Параллельные прямые циркулемСкачать

Две параллельные бесконечно длинные прямые нити
Решение:
Результирующее поле определяем по теореме косинусов
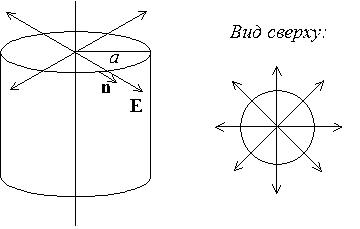
Поле бесконечно протяженной однородно заряженной нити
Модуль напряженности Ε результирующего электрического поля в точке, находящейся на расстоянии а от каждой нити.
Ответ:
💡 Видео
Математика это не ИсламСкачать

Параллельные прямые (задачи).Скачать

Поле заряженной нитиСкачать

Математика без Ху!ни. Уравнение плоскости.Скачать

Видеоурок "Параллельные прямые"Скачать

Геометрия 7 класс (Урок№33 - Повторение. Параллельные и перпендикулярные прямые.)Скачать

Теорема 13.2 Если две прямые параллельны третьей, то они параллельны ||Геометрия 7 класс||Скачать

10 класс, 5 урок, Параллельность трех прямыхСкачать

7 класс, 30 урок, Углы с соответственно параллельными или перпендикулярными сторонамиСкачать

10 класс, 4 урок, Параллельные прямые в пространствеСкачать

Электростатика | электрическое поле бесконечной нити (тонкого цилиндра)Скачать

Электрическое поле. Напряженность электрического поля. Силовые линии электрического поля. 10 класс.Скачать

Уравнение плоскости через 2 точки параллельно прямойСкачать

Математика без Ху!ни. Взаимное расположение прямой и плоскости.Скачать

Расстояние между параллельными прямымиСкачать

СОПРЯЖЕНИЕ ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ. [pairing parallel lines]Скачать
![СОПРЯЖЕНИЕ ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ. [pairing parallel lines]](https://i.ytimg.com/vi/f0vBNKACS2c/0.jpg)