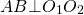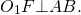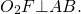Две окружности с центрами имеют общую хорду то прямая

Общая хорда двух пересекающихся окружностей перпендикулярна прямой, проходящей через центры этих окружностей.

Дано : окр. (O1; R) ∩ окр. (O2; r)=A, B.

Соединим центры окружностей с точками A и B. Обозначим точку пересечения прямой O1O2 с хордой AB как F.

Рассмотрим треугольники O1AO2 и O1BO2.

3) O1O2 — общая сторона.

Из равенства треугольников следует равенство соответствующих углов: ∠AO1F=BO1F, то есть O1F- биссектриса угла AO1B.

Треугольник AO1B — равнобедренный с основанием AB (O1A=O1B=R). Следовательно, биссектриса O1F является также его высотой и медианой. Таким образом,

Аналогично доказывается, что

По теореме о существовании и единственности прямой, перпендикулярной данной,через точку F можно провести только одну прямую, перпендикулярную данной прямой AB.

Следовательно, центры окружностей O1, O2 и точка F лежат на одной прямой O1O2, а общая хорда окружностей перпендикулярна этой прямой:

Видео:Две окружности | Резерв досрока ЕГЭ-2019. Задание 16. Профильный уровень | Борис Трушин |Скачать

Две окружности с центрами имеют общую хорду то прямая

№117 на рисунке 67 AB=BC, СD=DE. Докажите, что угол BAC= углу CED

№118 На основании BC равнобедренного треугольника ABC отмечены точки M и N так, что BM=CN. Докажите, что : а)треугольник BDE=треугольнику BDF б)треугольник ADE=треугольнику CDF

№119 В равнобедренном треугольнике DEK с основанием DK=16см отрезок EF-биссектриса, угол DEF=43градуса. Найдите KF,угол DEK, угол EFD

А) найти угол BNK

Б) Докожите ,что прямые MN и BK взаимно перпендикулярны

2. В равнобедренной трапеции тупой угол равен 135 градусов меньше основание равно 4 см, а высота 2 см найдите площадь трапеции?

3. Высота трапеции в 3 раза больше одного из оснований, но вдвое меньше другого. Найдите основания трапеции и высоту если площадь трапеции равна 168 см в квадрате?

Видео:Решение старой задачи ОГЭ №24Скачать

Помогите пожалуйста?

Геометрия | 5 — 9 классы

Докажите, что если две окружности имеют общую хорду, то прямая проходящая через центры окружности делят общую хорду пополам.

Все точки, равноудаленные от концов отрезка, лежат на перпендикуляре, проведенном через середину этого отрезка.

В случае этой хорды линия центров в 2 точках (в центрах окружностей) совпадает с этим перпендикуляром (ну, концы хорды лежат на окружностях, значит, они равноудалены от центров), а, значит, — совпадает везде (это одна из аксиом геометрии).

Поэтому линия центров двух окружностей, имеющих общую хорду, перпендикулярна этой общей хорде и делит её пополам.

Видео:Планиметрия 12 | mathus.ru | расстояние между центрами пересекающихся окружностейСкачать

Две окружности имеют общий центр?

Две окружности имеют общий центр.

Докажите, что хорды большей окружности, касающиеся меньшей окружности, равны между собой.

Видео:Радикальные оси для ЕГЭ профиль. Геометрические конструкции, убивающие №16Скачать

ПОМОГИТЕ, ПРОШУ?

Докажите, что прямая, проходящая через две точки пересечения двух окружностей, делит пополам отрезок, соединяющий точки касания этих окружностей с их общей касательной.

Видео:Математика ЕГЭ. С2. Два перпендикулярных сечения шара с общей хордойСкачать

Две окружности с равными радиусами пересекаются в двух точках, докажите, что отрезок, соединяющий центры окружностей, делит пополам их общую хорду?

Две окружности с равными радиусами пересекаются в двух точках, докажите, что отрезок, соединяющий центры окружностей, делит пополам их общую хорду.

Видео:Задание 24 Две пересекающиеся окружностиСкачать

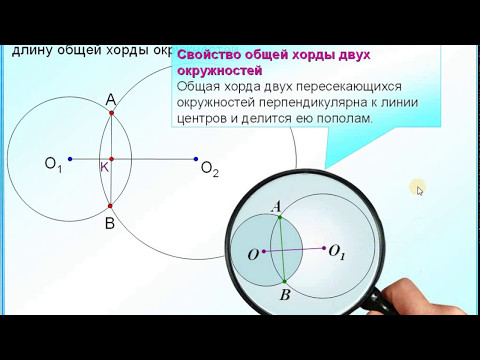
Докажите если две окружности имеют общую хорду, то прямая, проходящая через центры этих окружностей, перпендикулярна данной хорде?

Докажите если две окружности имеют общую хорду, то прямая, проходящая через центры этих окружностей, перпендикулярна данной хорде.

Видео:Геометрия Две окружности имеют единственную общую точку M. Через точку M проведены две прямыеСкачать

Радиус ОМ окружности с центром О делит хорду АВ пополам?

Радиус ОМ окружности с центром О делит хорду АВ пополам.

Докажите, что касательная, проведенная через точку М, параллельна хорде АВ.

Видео:Общая хорда двух окружностейСкачать

Докажите, что если две окружности имеют общую хорду, то прямая,проходящая через центры этих окружностей, перпендикулярна даннойхорде?

Докажите, что если две окружности имеют общую хорду, то прямая,

проходящая через центры этих окружностей, перпендикулярна данной

Видео:Геометрия Две окружности с центрами O1 и O3 и радиусами 4,5 и 2,5 касаются друг с другом внешнимСкачать

Две окружности с равными радиусами пересекаются в двух точках?

Две окружности с равными радиусами пересекаются в двух точках.

Докажите, что их общая хорда перпендикулярна к отрезку, соединяющему центры окружностей.

Видео:Геометрия 16-02. Взаимное расположение двух и более окружностей. Задача 2Скачать

Доказать, если две окружности имеют общую хорду, то прямая, проходящая через центры этих окружностей, делит общую хорду пополам?

Доказать, если две окружности имеют общую хорду, то прямая, проходящая через центры этих окружностей, делит общую хорду пополам.

Видео:ЕГЭ Задание 16 Три окружностиСкачать

Прямая l касается в точке M окружности с центром О?

Прямая l касается в точке M окружности с центром О.

Хорда AB параллельна l.

Доказать, что прямая OM делит хорду AB пополам.

Видео:Две окружности на плоскости. Математика. 6 класс.Скачать

Докажите, что перпендикуляр опущенный из центра окружности к хорде делит ее пополамПОМОГИТЕ?

Докажите, что перпендикуляр опущенный из центра окружности к хорде делит ее пополам

Вы перешли к вопросу Помогите пожалуйста?. Он относится к категории Геометрия, для 5 — 9 классов. Здесь размещен ответ по заданным параметрам. Если этот вариант ответа не полностью вас удовлетворяет, то с помощью автоматического умного поиска можно найти другие вопросы по этой же теме, в категории Геометрия. В случае если ответы на похожие вопросы не раскрывают в полном объеме необходимую информацию, то воспользуйтесь кнопкой в верхней части сайта и сформулируйте свой вопрос иначе. Также на этой странице вы сможете ознакомиться с вариантами ответов пользователей.

Пусть в треугольнике ABC известны стороны AB = c, BC = b и медиана BM = m. На луче AM отложим отрезок MD, MD = AM и соединим точку D с точками B и C. Поскольку в полученном четырехугольнике ABCD диагонали точкой пересечения делятся пополам, то ABCD..

∠АВС = ∠А₁АС + ∠С₁СА ∠А₁АС = ∠С₁СА = х х + х + 130 = 180 2х + 130 = 180 2х = 180 — 130 2х = 50 х = 25 = ∠А₁АС = ∠С₁СА Тогда : ∠АВС = 25 + 25 = 50 Пусть ∠А = ∠С = у Тогда : у + у + 50 = 180 2у + 50 = 180 2у = 130 у = 65 = ∠А = ∠С ∠АА₁В = 180 — (ВАА₁ +..

Весь циферблат равен 360°. Каждые 5 минут — это 30° (360 : 12 = 30). 5 час — это отсек 25 минуты. Так же известно, что есть 10 минут. Получается, что угол занимает по три пятиминутки ((25 — 10) : 5 = 3) Узнаём градусную меру : 3•30° = 90°.

Большая дуга относится к меньшей как 4 : 1. Т. е. Большая дуга — 4 части, меньшая — 1 часть. Вся окружность — 5 частей. Градусная мера окружности 360°, откуда 1 часть = 360° : 5 = 72°. Это меньшая дуга. Большая дуга = 72 * 4 = 288°. Ответ : 72..

По теореме Пифагора : смНайдем синус угла B : sinB = AC / AB = 5 / 10 = 1 / 2значит, В = 30 градусов.

ABCD — трапеция (буквы можешь расположить, как хочешь)AC — диагональBC = 10L ACB = L DL CAD = L ACB (по свойству трапеции) — — — — — — > L D = L CAD — — — — — > AC = CDL ACB = L CAD — — — — — > L BAD = 90 град. — — — — > L D = L CAD = L ACB = 90 2..

M(x1 ; y1) n(x2 ; y2) середина = ((x2 — x1) / 2 ; (y2 — y1) / 2) 1) (5 ; 2) 2)(1 ; 3) 3)(1, 5 ; 4, 5).

S = 6 * 10 * 8 * 20 = 9600 Вот.

Всё 12 ребер у куба равны. Найдем длину одного : 48 : 12 = 4 Все 6 граней — равные квадраты. Тогда площадь S = 6 * 4² = 6 * 16 = 96.

📺 Видео

Геометрия Общая хорда двух пересекающихся окружностей видна из их центров под углами 90 и 60. НайтиСкачать

Окружность, диаметр, хорда геометрия 7 классСкачать

[7] Окружности с нуля для ЕГЭ по математике. Внешнее касание окружностей. Конструкция из демоверсии.Скачать

ЕГЭ задание 16Скачать

[10] Окружности с нуля для ЕГЭ по математике. Линия центров перпендикулярна общей хорде и делит...Скачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

Касание окружностей | Задачи 1-10 | Решение задач | Волчкевич | Уроки геометрии 7-8 классСкачать

Две окружности. ОГЭ. Задача 26. Дополнительные построенияСкачать