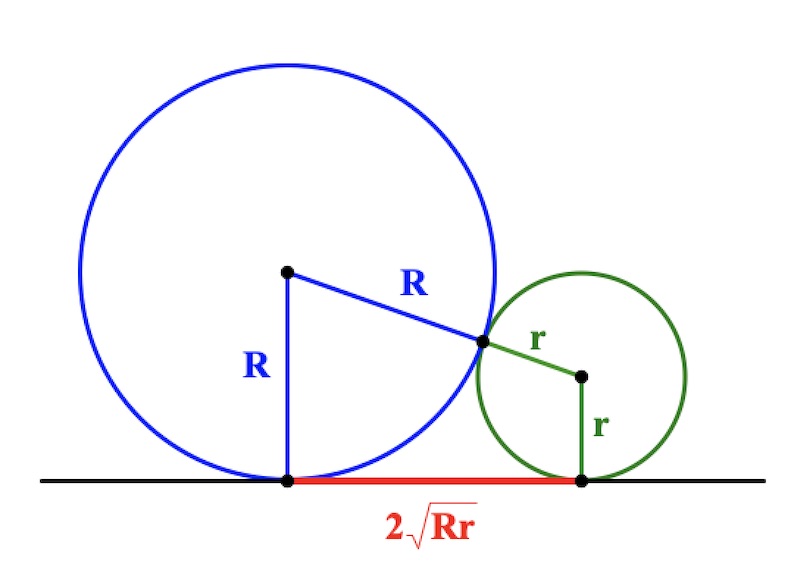
Общие касательные к двум окружностям
 Взаимное расположение двух окружностей |
| Общие касательные к двум окружностям |
| Формулы для длин общих касательных и общей хорды |
| Доказательства формул для длин общих касательных и общей хорды |
- Взаимное расположение двух окружностей
- Формулы для длин общих касательных и общей хорды двух окружностей
- Доказательства формул для длин общих касательных и общей хорды двух окружностей
- Две окружности касаются внешним образом и имеют общую касательную
- Теорема о длине внешней общей касательной к окружностям
- 📺 Видео
Видео:Окружности касаются внешним образом #егэ2023 #математика #егэ #школа #shorts #fypСкачать
Взаимное расположение двух окружностей
| Фигура | Рисунок | Свойства |
| Две окружности на плоскости |  | |
| Каждая из окружностей лежит вне другой |  | |
| Внешнее касание двух окружностей |  | |
| Внутреннее касание двух окружностей |  | |
| Окружности пересекаются в двух точках |  |  |
| Каждая из окружностей лежит вне другой | ||
| ||
| Внешнее касание двух окружностей | ||
| ||
| Внутреннее касание двух окружностей | ||
| ||
| Окружности пересекаются в двух точках | ||
| ||
| ||
| Каждая из окружностей лежит вне другой | ||
Расстояние между центрами окружностей больше суммы их радиусов | ||
| Внешнее касание двух окружностей | ||
Расстояние между центрами окружностей равно сумме их радиусов | ||
| Внутреннее касание двух окружностей | ||
| Окружности пересекаются в двух точках | ||
Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов r1 – r2 лежит внутри другой | ||
| Внутренняя касательная к двум окружностям |  | |
| Внутреннее касание двух окружностей |  | |
| Окружности пересекаются в двух точках |  | |
| Внешнее касание двух окружностей |  | |
 | ||
 | ||
| Внешняя касательная к двум окружностям | |
 | |
| Внутренняя касательная к двум окружностям | |
| |
| Внутреннее касание двух окружностей | |
| |
| Окружности пересекаются в двух точках | |
| |
| Внешнее касание двух окружностей | |
| |
| |
| Каждая из окружностей лежит вне другой | |
| |
| Внешняя касательная к двум окружностям | ||||||||||||||||||||||||||||
| Внутренняя касательная к двум окружностям | ||||||||||||||||||||||||||||
| Внутреннее касание двух окружностей | ||||||||||||||||||||||||||||
| Окружности пересекаются в двух точках | ||||||||||||||||||||||||||||
| Внешнее касание двух окружностей | ||||||||||||||||||||||||||||
| Каждая из окружностей лежит вне другой | ||||||||||||||||||||||||||||
| Фигура | Рисунок | Формула | |||||||||||||||||||
| Внешняя касательная к двум окружностям |  | ||||||||||||||||||||
| Внутренняя касательная к двум окружностям |  | ||||||||||||||||||||
| Общая хорда двух пересекающихся окружностей |  | ||||||||||||||||||||
| Внешняя касательная к двум окружностям | |||||||||||
| |||||||||||
| Внутренняя касательная к двум окружностям | |||||||||||
| |||||||||||
| Общая хорда двух пересекающихся окружностей | |||||||||||
| |||||||||||
| Внешняя касательная к двум окружностям | |||||||
| Внутренняя касательная к двум окружностям | |||||||
| Общая хорда двух пересекающихся окружностей | |||||||
Длина общей хорды двух окружностей вычисляется по формуле
Видео:Две окружности | Резерв досрока ЕГЭ-2019. Задание 16. Профильный уровень | Борис Трушин |Скачать  Доказательства формул для длин общих касательных и общей хорды двух окружностейУтверждение 1 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d (рис.1), то длина общей внешней касательной к этим окружностям вычисляется по формуле
что и требовалось доказать. Утверждение 2 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d , то длина общей внутренней касательной к этим окружностям вычисляется по формуле
что и требовалось доказать. Утверждение 3 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d , то длина общей хорды AB этих окружностей вычисляется по формуле
Доказательство . Для того, чтобы найти длину общей хорды AB двух окружностей, введём, как показано на рисунке 3, Видео:две окружности касаются внешним образом в точке КСкачать  Две окружности касаются внешним образом и имеют общую касательнуюДве окружности касаются внешним образом в точке K. Прямая AB касается первой окружности в точке A, а второй — в точке B. Прямая BK пересекает первую окружность в точке D, прямая AK пересекает вторую окружность в точке C. а) Докажите, что прямые AD и BC параллельны. б) Найдите площадь треугольника AKB, если известно, что радиусы окружностей равны 4 и 1. а) Обозначим центры окружностей O1 и O2 соответственно. Пусть общая касательная, проведённая к окружностям в точке K, пересекает AB в точке M. По свойству касательных, проведённых из одной точки, AM = KM и KM = BM. Треугольник AKB, у которого медиана равна половине стороны, к которой она проведена, — прямоугольный. Вписанный угол AKD прямой, поэтому он опирается на диаметр AD. Значит, AD ⊥ AB. Аналогично получаем, что BC ⊥ AB. Следовательно, прямые AD и BC параллельны. б) Пусть, для определенности, первая окружность имеет радиус 4, а радиус второй равен 1. Треугольники BKC и AKD подобны, У треугольников AKD и AKB общая высота, следовательно, Вычислим площадь трапеции ABCD. Заметим, что Тогда Следовательно, 25S = 20, откуда S = 0,8 и SAKB = 4S = 3,2. Приведем вариант решения п. б) предложенный Рамилем Багавиевым. Из первого решения известно, что Теперь несложно вычислить
|
Пусть 
тогда 
то есть SAKB = 4S. Аналогично, SCKD = 4S. Площадь трапеции ABCD равна 25S.
Проведём к AD перпендикуляр O2H, равный высоте трапеции, и найдём его из прямоугольного треугольника O2HO1: 
Из подобия треугольников AKD и AKB следует 
таким образом AK = 2BK. Напишем теорему Пифагора для треугольника AKB 
