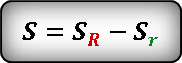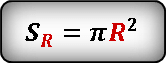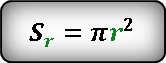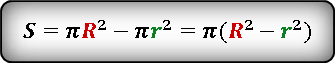Две окружности имеют общий центр образуют кольцо

Видео:Геометрия 9 класс (Урок№10 - Взаимное расположение двух окружностей.)Скачать

Условие задачи:

Две окружности, имеющие общий центр, образуют кольцо. Радиус внешней окружности равен 10 см, а внутренней 8 см. Найти площадь этого кольца.

Дано:
Радиус внешней окружности, R = 10 см
Радиус внутренней окружности, r = 8 см

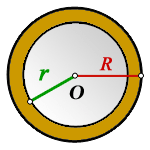
Пояснение к рисунку:
O — общий центр окружностей

Видео:9 класс, 8 урок, Взаимное расположение двух окружностейСкачать

Найти площадь кольца: S

Площадь кольца можно выразить как разницу между площадями внешнего круга и внутреннего.

Формула площади внешнего круга.

Формула площади внутреннего круга.

После подстановки и преобразования, получаем следующее выражение для площади кольца.

Видео:Взаимное расположение двух окружностей. Урок 8. Геометрия 9 классСкачать

Ответ:

Результат получился приблизительным, потому что число π нельзя выразить точно, оно имеет бесконечное количество знаков после запятой. В данном случаи, мы взяли π ≈ 3.14

Видео:Две окружности на плоскости. Математика. 6 класс.Скачать

Найдите площадь кольца образованного двумя окружностями

Видео:Взаимное расположение двух окружностей.Использование уравнений окружности и прямой при решении задачСкачать

Площадь кольца

Видео:Найти центр и радиус окружностиСкачать

Онлайн калькулятор

Площадь кольца по радиусам или диаметрам

Чему равна площадь кольца ограниченного двумя окружностями, если:

у внешней окружности
у внутренней окружности

Площадь кольца по толщине и любому другому параметру

Чему равна площадь кольца ограниченного двумя окружностями, если:

толщина кольца t =

Видео:Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Теория

Площадь кольца через радиусы

Чему равна площадь кольца S ограниченного двумя окружностями, если известны радиус внешней окружности R и радиус внутренней окружности r ?

Формула

Пример

К примеру, определим площадь кольца, у которого внешний радиус R = 3 см, а внутренний радиус r = 2 см:

S = 3.14 ⋅ (3² — 2²) = 3.14 ⋅ (9 — 4) = 3.14 ⋅ 5 = 15.7 см²

Ответ: S = 15.7 см²

Площадь кольца через диаметры

Чему равна площадь кольца S ограниченного двумя окружностями, если известны диаметр внешней окружности D и диаметр внутренней окружности d ?

Формула

Пример

К примеру, определим площадь шайбы, внешний диаметр которой D = 4 см, а внутренний – d = 2 см:

S = 3.14 / 4 ⋅ (4² — 2²) = 0.785 ⋅ (16 — 4) = 9.42 см²

Ответ: S = 9.42 см²

Площадь кольца через толщину

Чтобы посчитать площадь кольца S зная его толщину t, необходимо знать ещё какой-нибудь из следующих параметров:

• внешний диаметр D
• внутренний диаметр d
• радиус внешней окружности R
• радиус внутренней окружности r

Формулы

Пример

Для примера, найдём чему равна площадь кольца толщиной t = 2 см и внешним диаметром D = 5 см:

S = 3.14/4 ⋅ (5² — (5 — 2 ⋅ 2)²) = 0.785 ⋅ (25 — 1) = 18.84 см²

Видео:Взаимное расположение окружностей. 7 класс.Скачать

Задача: определить площадь кольца, если известны радиусы

Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Условие задачи:

Две окружности, имеющие общий центр, образуют кольцо. Радиус внешней окружности равен 10 см, а внутренней 8 см. Найти площадь этого кольца.

Дано:
Радиус внешней окружности, R = 10 см
Радиус внутренней окружности, r = 8 см

Пояснение к рисунку:
O — общий центр окружностей

Видео:7 класс. Геометрия. Взаимное расположение двух окружностей. 28.04.2020.Скачать

Найти площадь кольца: S

Площадь кольца можно выразить как разницу между площадями внешнего круга и внутреннего.

Формула площади внешнего круга.

Формула площади внутреннего круга.

После подстановки и преобразования, получаем следующее выражение для площади кольца.

Видео:Определение центра дуги окружности, построение окружности по 3 точкамСкачать

Ответ:

Результат получился приблизительным, потому что число π нельзя выразить точно, оно имеет бесконечное количество знаков после запятой. В данном случаи, мы взяли π ≈ 3.14

Видео:Уравнение окружности (1)Скачать

Найдите площадь кольца, ограниченного двумя окружностями с общим центром и радиусами R1 и R2, R12

Видео:✓ Как найти второй радиус? | Ботай со мной #105 | Борис ТрушинСкачать

Ваш ответ

Видео:ГЕОМЕТРИЯ 9 класс: Уравнение окружности и прямойСкачать

решение вопроса

Видео:Внешнее сопряжение дуги и прямой дугой заданного радиуса. Урок16.(Часть1.ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Похожие вопросы

• Все категории
• экономические 43,277
• гуманитарные 33,618
• юридические 17,900
• школьный раздел 606,882
• разное 16,829

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:№8. Верно ли утверждение: а) если две точки окружности лежат в плоскостиСкачать

Найдите площадь кольца, расположенного между двумя окружностями, имеющими общий центр, радиусы которых равны 4 см и 6 см

Видео:КАСАЮЩИЕСЯ ОКРУЖНОСТИ. # ЕГЭ 2023Скачать

Ваш ответ

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

решение вопроса

Видео:5 класс, 22 урок, Окружность и кругСкачать

Похожие вопросы

• Все категории
• экономические 43,280
• гуманитарные 33,618
• юридические 17,900
• школьный раздел 606,971
• разное 16,829

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

🎦 Видео

Пара фактов про окружность | Ботай со мной #067 | Борис Трушин |Скачать