Две касающиеся окружности вписанной в угол 60

Видео:Задание 26 Две окружности, вписанные в угол Внешнее касаниеСкачать

Две окружности вписанные в угол касаются

Две касающиеся внешним образом в точке K окружности, радиусы которых равны 33 и 39, вписаны в угол с вершиной A. Общая касательная к этим окружностям, проходящая через точку K, пересекает стороны угла в точках B и C. Найдите радиус окружности, описанной около треугольника ABC.

Пусть Q — центр большей окружности, а O — центр меньшей, QM и ON — радиусы, проведённые в точки касания окружностей с прямой AC, S — центр окружности, описанной около треугольника ABC , r — радиус окружности, описанной около треугольника ABC.

Поскольку BC и AB — общие касательные к окружностям, BO и BQ — биссектрисы углов ABK и смежного с ним. Значит, угол OBQ прямой, следовательно, из треугольника OBQ находим, что .

Пусть AN = x . Прямоугольные треугольники ANO и AMQ подобны с коэффициентом , значит, ,

Отрезки MC , CK и CN равны как отрезки касательных, проведённых из

одной точки, значит, , , откуда

В прямоугольном треугольнике ABK находим неизвестный катет:

В прямоугольном треугольнике SBK по теореме Пифагора имеем

;

Видео:Геометрия В острый угол, равный 60, вписаны две окружности, извне касающиеся друг друга. РадиусСкачать

Две окружности вписанные в угол 60 градусов касаются друг друга внешним образом найти расстояние от точки касания окружности до стороны угла?

Геометрия | 5 — 9 классы

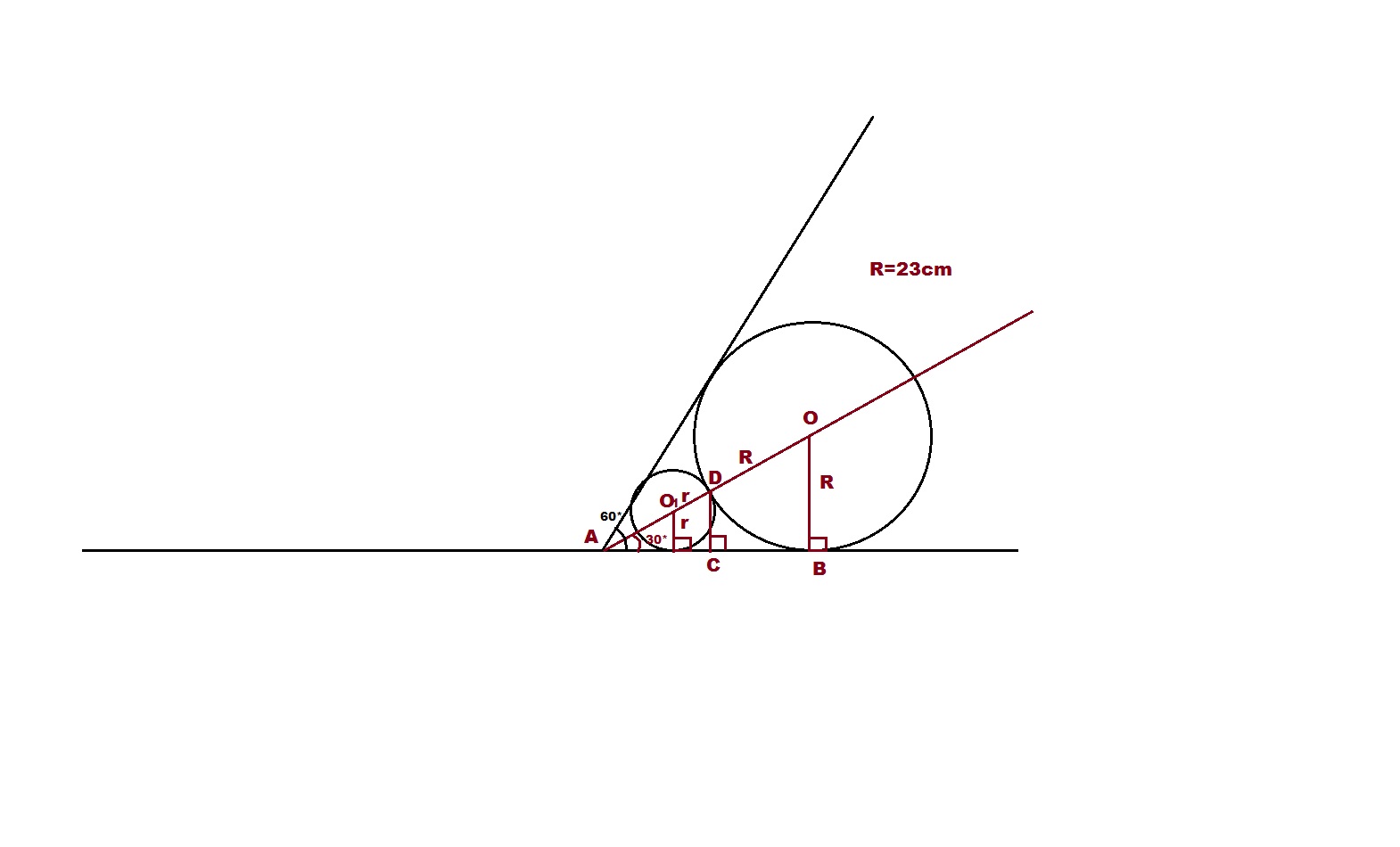
Две окружности вписанные в угол 60 градусов касаются друг друга внешним образом найти расстояние от точки касания окружности до стороны угла.

Радиус большей окружности 23.

1) расмотрим тр — ки АОВ и АДС — прямоугольные (ОВ _|_AB радиус к касательной .

DC_|_AB — ОВ \ \ СД ) , подобные по2 углам(угАОВ — общий, угВ = угС = 90 *

угОАВ = 30 * ( АО — биссектриса содержащая центры вписаных окр) ,

ОВ = OD = R = 23cm

напротив угла в 30 * лежит катет в 1 / 2гипотенузы, значт АО = 46см, АД = 46 — R = 23cm

коэффиц подобия к = АО / АД = 2

ОВ / ДС = к = 2 ДС = 23 / 2 = 11, 5см.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Две касающиеся внешним образом окружности с центрами в точках О и О1 касаются сторон угла А( В и В1 — точки касания)?

Две касающиеся внешним образом окружности с центрами в точках О и О1 касаются сторон угла А( В и В1 — точки касания).

Расстояние между точками А и О1 в два раза меньше, чем расстояние между центрами окружностей.

Найдите радиус О1В1 если радиус ОВ равен 24 см.

Видео:В угол, равный 60, вписаны две окружности, причём эти окружности касаются друг другаСкачать

Две окружности касаются друг друга внешним образом в точке M?

Две окружности касаются друг друга внешним образом в точке M.

Общая внешняя касательная к этим окружностям касается их в точках A и B, причем MA = 8 ; MB = 6.

Определите радиусы окружностей.

Видео:Задача 6 №27859 ЕГЭ по математике. Урок 104Скачать

Две окружности, каждая из которых вписана в острый угол 60 градусов, касаются друг друга внешним образом?

Две окружности, каждая из которых вписана в острый угол 60 градусов, касаются друг друга внешним образом.

Найдите расстояние от точки касания окружностей до стороны угла, если радиус большей окружности равен 23.

Видео:ЕГЭ Задание 16 Окружности вписанные в уголСкачать

1. Из точки А окружности проведены диаметр АВ и АС, которая продолжена за точку С на расстояние СК, равное АС?

1. Из точки А окружности проведены диаметр АВ и АС, которая продолжена за точку С на расстояние СК, равное АС.

Найти ВС, если КВ = 10 и &lt ; САВ = 30

Две окружности, каждая из которых вписана в острый угол 60, касаются друг друга внешним образом.

Найти расстоние от точки касания окружностей до стороны угла, если радиус большей окружности равен 23.

3. В круговой сектор вписана окружность, радиус которой в три раза меньше радиуса сектора.

Найти величину центрального угла.

Видео:Нафиг теорему синусов 3 задание проф. ЕГЭ по математике (часть II)Скачать

В угол 120 градусов вписана окружность радиуса 8 см?

В угол 120 градусов вписана окружность радиуса 8 см.

Найдите расстояние между точками касания окружности со сторонами угла.

Видео:Две окружности | Резерв досрока ЕГЭ-2019. Задание 16. Профильный уровень | Борис Трушин |Скачать

Три равных окружности радиуса R касаются друг друга внешним образом ?

Три равных окружности радиуса R касаются друг друга внешним образом .

Найдите стороны и угл треугольника , вершинами которого служат точки касания .

Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Две касающихся внешним образом в точке К окружности, радиусы которых = 6и24, вписаны в угол с вершиной А?

Две касающихся внешним образом в точке К окружности, радиусы которых = 6и24, вписаны в угол с вершиной А.

Общая касательная к этим окружностям, проходящая через точку К, пересекает стороны угла в точках В и С, Найдите радиус окружности, описанной около треугольника АВС.

Видео:ОГЭ по математике. Задача 26Скачать

В угол равный 120 град вписана окружность радиуса 8 см?

В угол равный 120 град вписана окружность радиуса 8 см.

Найдите расстояние между точками касания окружности со сторонами угла.

Видео:ОГЭ Задание 26 Внешнее касание двух окружностейСкачать

Две окружности с радиусами 3 см и 6 см касаются друг друга внешним образом чему равно расстояние Между центрами окружностей?

Две окружности с радиусами 3 см и 6 см касаются друг друга внешним образом чему равно расстояние Между центрами окружностей.

Видео:ЕГЭ Задание 16 Две окружностиСкачать

Две окружности радиусами R и r касаются внешним образом в точке M?

Две окружности радиусами R и r касаются внешним образом в точке M.

К окружностям проведена общая внешняя касательная NK, где N и K — точки касания.

В криволенейный треугольник MNK вписана окружность.

Найдите ее радиус.

На этой странице сайта вы найдете ответы на вопрос Две окружности вписанные в угол 60 градусов касаются друг друга внешним образом найти расстояние от точки касания окружности до стороны угла?, относящийся к категории Геометрия. Сложность вопроса соответствует базовым знаниям учеников 5 — 9 классов. Для получения дополнительной информации найдите другие вопросы, относящимися к данной тематике, с помощью поисковой системы. Или сформулируйте новый вопрос: нажмите кнопку вверху страницы, и задайте нужный запрос с помощью ключевых слов, отвечающих вашим критериям. Общайтесь с посетителями страницы, обсуждайте тему. Возможно, их ответы помогут найти нужную информацию.

АО = СО, ВО = ДО (по условию), угол АОВ = углу СОД (вертикальные), следовательно трегольники равны по 1 признаку.

А властивістю дотичних, проведених до кола з однієї точки, маємо : AM = AN, BM = ВК, СК = CN. AN = AM. Р = АВ + ВС + АС. АВ = AM + MB, ВС = ВК + КС, АС = AN + NС. Р = AM + MB + ВК + КС + AN + NC ; P = 2(ВК + КС + AM) ; р = ВК + КС + AM ; р = ВС +..

Отложим на сторонеABотрезокBD, равныйBC. Тогда треугольникBCD– равнобедренный с углом при вершине 20°, поэтому углы при основании равны 80° (см. Рис. ). ПустьCE– биссектриса углаC. Тогда ∠BCE = 60°, поэтому ∠AEC = 20° + 60° = 80°. Таким образом.

SZ = 2. 5 TU = 5. 35 мне кажется что так.

Всего существует три варианта размещения в пространстве двух плоскостей. — они параллельны и тогда нет ни одной общей точки — они пересекаются и тогда любые три точки, выбранные на линии пересечения являются общими для этих плоскостей — они совпадаю..

Так как сумма углов треугольника равна 180 градусов, значит 180 — 55 = 125градусов.

Угол А = 180 — 120 = 60, BE — биссектриса, следовательно угол АВЕ = 60, а так как сумму внутренних углов 180 градусов то угол АЕВ = 180 + 60 + 60 = 60, если в треугольнике все углы одинаковые то он равностороний, следовательно АЕ = ВЕ = АВ = 6, Р = 2..

S = 18 га = 180 000 м² а = S / в = 180000 / 200 = 900 м.

Видео:Задание 26 Две окружности, внешнее касаниеСкачать

Задача 45619 Две касающиеся внешним образом в точке К.

Условие

Две касающиеся внешним образом в точке К окружности, радиус одной из которых вдвое больше радиуса другой, вписаны в угол с вершиной А. Общая касательная к этим окружностям, проходящая через точку К, пересекает стороны угла в точках В и С.

а) Докажите, что АВ = АС.
б) Найдите радиус окружности, описанной около треугольника АВС, если АВ = sqrt(3). [16п2]

Все решения

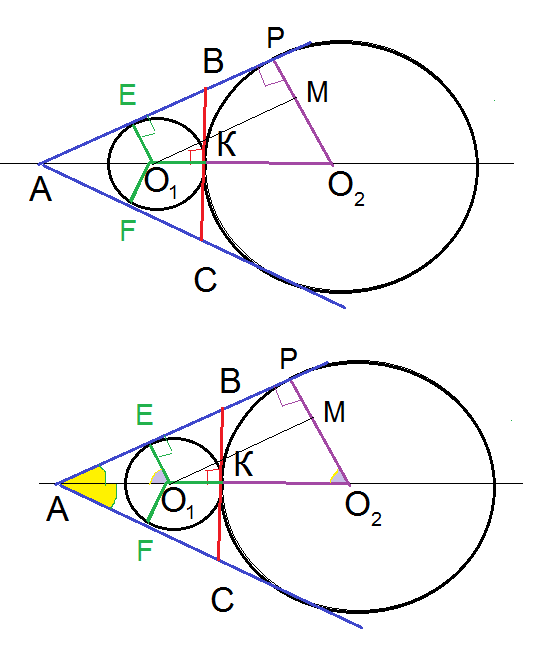
Две окружности вписаны в угол с вершиной А.
Радиусы O_(1)E и O_(1)F, проведенные в точки касания , [i]перпендикулярны [/i]сторонам угла.

По [i]свойству касательных[/i] к окружности, проведенных из одной точки, отрезки касательных равны:
[red]АE[/red]=[red]АF[/red]
и образуют [i]равные углы [/i]с прямой, проходящей через вершину А и центры окружностей.
Значит
центры O_(1) и O_(2) лежат на [i]биссектрисе[/i] угла А

BC — касательная к этим окружностям, проходящая через точку К,
значит О_(1)K ⊥ BC

AK — биссектриса и высота треугольника АВС, значит Δ АВС — равнобедренный и [b]АВ=АС[/b].

и AK — медиана Δ АВС ⇒ BK=CK

Прямоугольные треугольники
Δ AEO_(1)

Δ APO_(2) по двум углам
( ∠ EAO_(2)- общий)
⇒ [b]∠ АО_(1)E= ∠ AO_(2)P [/b]

O_(1)EPO_(2) — прямоугольная трапеция.
O_(1)E=r
O_(2)E=2r

Δ AEO_(1)= Δ O_(1)MO_(2) ⇒ [b] AO_(1)[/b]=O_(1)O_(2)=[b]3r[/b]

По теореме Пифагора из треугольника АВК

R=AB*BC*AC/4S_( Δ ABC)= AB^2/2AK=3/2sqrt(21/8)=sqrt(6/7)

О т в е т. [m]\sqrt\frac [/m]

🔍 Видео

Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

✓ Как найти второй радиус? | Ботай со мной #105 | Борис ТрушинСкачать

Из точки A проведены две касательные к окружности ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Вписанная и описанная окружность - от bezbotvyСкачать

ТОП-3 конструкции с окружностями для №16 из ЕГЭ 2023 по математикеСкачать

Окружности касаются внешним образом #егэ2023 #математика #егэ #школа #shorts #fypСкачать

Из точки A проведены две касательные к окружности ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать