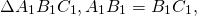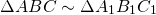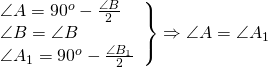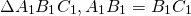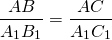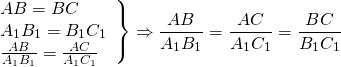Два равнобедренных треугольника подобны

Какие из следующих утверждений верны?

1) Если катет и гипотенуза прямоугольного треугольника равны соответственно 6 и 10, то второй катет этого треугольника равен 8.

2) Любые два равнобедренных треугольника подобны.

3) Любые два прямоугольных треугольника подобны.

4) Треугольник ABC, у которого AB = 3, BC = 4, AC = 5, является тупоугольным.

Если утверждений несколько, запишите их номера в порядке возрастания.

Проверим каждое из утверждений.

1) «Если катет и гипотенуза прямоугольного треугольника равны соответственно 6 и 10, то второй катет этого треугольника равен 8.»— верно, по теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов.

2) «Любые два равнобедренных треугольника подобны.» — неверно, так как углы, заключенные между пропорциональными сторонами, не равны.

3) «Любые два прямоугольных треугольника подобны.» — неверно, так как нет второго равного угла.

4) «Треугольник ABC, у которого AB = 3, BC = 4, AC = 5, является тупоугольным.» — неверно, треугольник с такими сторонами является прямоугольным.

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Подобные треугольники

Видео:№561. Докажите, что два равносторонних треугольника подобны.Скачать

Определение

Подобные треугольники — треугольники, у которых углы соответственно равны, а стороны одного соответственно пропорциональны сторонам другого треугольника.

Коэффициентом подобия называют число k , равное отношению сходственных сторон подобных треугольников.

Сходственные (или соответственные) стороны подобных треугольников — стороны, лежащие напротив равных углов.

Видео:Любые два равносторонних треугольника подобны. | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

Признаки подобия треугольников

I признак подобия треугольников

Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.

II признак подобия треугольников

Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.

Видео:Подобие треугольников (ч.2) | Математика | TutorOnlineСкачать

Свойства подобных треугольников

• Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
• Отношение периметров подобных треугольников равно коэффициенту подобия.
• Отношение длин соответствующих элементов подобных треугольников (в частности, длин биссектрис, медиан, высот и серединных перпендикуляров) равно коэффициенту подобия.

Видео:Геометрия Докажите, что два равнобедренных треугольника подобны, если углы при их вершинах равныСкачать

Примеры наиболее часто встречающихся подобных треугольников

1. Прямая, параллельная стороне треугольника, отсекает от него треугольник, подобный данному.

2. Треугольники и , образованные отрезками диагоналей и основаниями трапеции, подобны. Коэффициент подобия –

3. В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобных исходному.

Здесь вы найдете подборку задач по теме «Подобные треугольники» .

Видео:Всё про прямоугольный треугольник за 15 минут | Осторожно, спойлер! | Борис Трушин !Скачать

Равнобедренные треугольники подобны

Выясним, в каких случаях равнобедренные треугольники подобны.

Признаки подобия равнобедренных треугольников

1) Если угол между боковыми сторонами одного равнобедренного треугольника равен углу между боковыми сторонами другого равнобедренного треугольника, то такие треугольники подобны.

Дано : ∆ ABC, AB=BC,

Из равенства углов при вершине равнобедренных треугольников следует равенство их углов при основаниях:

Следовательно, треугольники ABC и A1B1C1 подобны по двум углам.

Что и требовалось доказать .

2) Если угол между основанием и боковой стороной одного равнобедренного треугольника равен углу между между основанием и боковой стороной другого равнобедренного треугольника, то такие треугольники подобны.

Дано : ∆ ABC, AB=BC,

Так как углы при основании равнобедренного треугольника равны, в треугольнике ABC ∠A=∠C, в треугольнике A1B1C1∠A1=∠C1. Следовательно, треугольники ABC и A1B1C1 подобны по двум углам.

Что и требовалось доказать .

3) Если основание и боковая сторона одного равнобедренного треугольника пропорциональны основанию и боковой стороне другого равнобедренного треугольника, то такие треугольники подобны.

Дано : ∆ ABC, AB=BC,

Следовательно, треугольники ABC и A1B1C1 подобны по трём сторонам.

🔍 Видео

Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать

№553. Подобны ли равнобедренные треугольники, если они имеют: а) по равному острому углуСкачать

Задание № 553 — Геометрия 8 класс (Атанасян)Скачать

№110. Докажите, что если медиана треугольника совпадает с его высотой, то треугольникСкачать

Равнобедренный треугольник. 7 класс.Скачать

Как ПОНЯТЬ ГЕОМЕТРИЮ за 5 минут — Подобие ТреугольниковСкачать

Самая простая нерешённая задача — гипотеза Коллатца [Veritasium]Скачать

✓ Свойства и признаки равнобедренного треугольника | Ботай со мной #008 | Борис ТрушинСкачать

Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Равнобедренный треугольник. Определение. Свойства. Теоремы и доказательства.Скачать

7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать

Геометрия 7 класс (Урок№13 - Равнобедренный треугольник.)Скачать

№107. В равнобедренном треугольнике основание в два раза меньше боковой стороны, а периметрСкачать

Все равнобедренные треугольники подобны. | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать