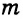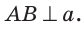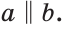Определение.1. Параллельные прямое
Определение.2. Перпендикулярные прямые
Теорема.1. I свойство параллельных прямых
Теорема.2. II свойство параллельных прямых
Теорема.3. III свойство параллельных прямых
Теорема.4. IV свойство параллельных прямых
Теорема.5. V свойство параллельных прямых
Теорема.6. I признак параллельных прямых
Теорема.7. II признак параллельных прямых
Теорема.8. III признак параллельных прямых
Теорема.9. IV признак параллельных прямых
Теорема 10. V признак параллельных прямых
Теорема 11. Две прямые, параллельные третей
Теорема 11.1 Следствие
Теорема 12. Прямая, пересекающая одну из параллельных прямых
Теорема 13. Отрезки параллельных прямых
Теорема 14. Теорема Фалеса
Теорема 14.1. Параллельные прямые, пересекающие стороны угла
Теорема 15. Прямая, перпендикулярна одной из параллельных прямых
Теорема 16. Две (и более) прямые, перпендикулярные третей прямой
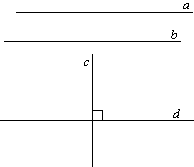
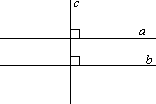
Определение 1. Параллельными называются прямые, которые не пересекаются, сколько бы мы их не продолжали.
На рисунке a и b.
Определение 2. Перпендикулярными называются прямые, которые пересекаются под прямым углом.
На рисунке c и d.
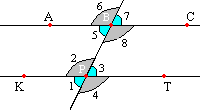
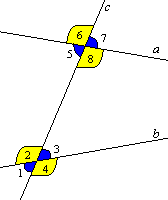
Внутренние накрестлежащие углы — 2 и 8; 3 и 5
Внешние накрестлежащие углы — 1 и 7; 4 и 6
Внутренние односторонние углы — 2 и 5; 3 и 8
Внешние односторонние углы — 1 и 6; 4 и 7
Соответственные углы — 1 и 5; 2 и 6; 3 и 7; 4 и 8
Между этими углами можно вывести закономерности. Свойства параллельных прямых:
Теорема 1. Внутренние накрестлежащие углы равны
Доказательство: Пусть a и b — две параллельные прямые, c — секущая, A и B — точки пересечения секущей с этими прямыми. Пусть утверждение теоремы ложно. Проведем тогда через точку A прямую d, такую что внутренние накрест лежащие углы при прямых b и d и секущей c равны. Тогда по первому признаку параллельности прямых, прямые b и d параллельны. Но прямые b и a параллельны. Значит, через точку A проходят две прямые — a и d, параллельные прямой b. Это противоречит IX аксиоме. Значит, утверждение теоремы верно. Теорема доказана.
Теорема 2. Внешние накрестлежащие углы равны
Доказательство: Очевидно из первого свойства параллельных прямых.
Теорема 3. Сумма внутренних односторонних углов равна 180 градусам
Доказательство: Очевидно из первого свойства параллельных прямых.
Теорема 4. Сумма внешних односторонних углов равна 180 градусам
Доказательство: Очевидно из первого свойства параллельных прямых.
Теорема 5. Соответственные углы равны
Доказательство: Очевидно из первого свойства параллельных прямых.
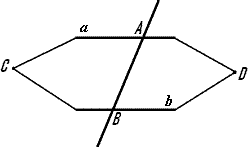
Теорема 6. Если при пересечении двух прямых а и b третей прямой с внутренние накрестлежащие углы равны (одна пара), то такие прямые а и b являются параллельными
Доказательство: Пусть прямые a и b пересекаются секущей в точках A и B, но прямые a и b пересекаются в точке C (рис. 15). Секущая c разбивает плоскость на две полуплоскости. В одной из них лежит точка C. Построим треугольник ABD, равный треугольнику ABC, с вершиной D в другой полуплоскости. Угол DAB равен углу ABC, а значит, точка D лежит на прямой a по условию. Аналогично точка D лежит на прямой b. Следовательно, точка D принадлежит прямым a и b. Значит, прямые a и b пересекаются в двух точках — C и D. Противоречие. Значит, исходное предположение не верно. Теорема доказана.
Теорема 7. Если при пересечении двух прямых а и b третей прямой с внешние накрестлежащие углы равны (одна пара), то такие прямые а и b являются параллельными
Доказательство: Очевидно из первого признака параллельности прямых.
Теорема 8. Если при пересечении двух прямых а и b третей прямой с сумма внутренних односторонних углов равна 180 градусам (одна пара), то такие прямые а и b являются параллельными
Доказательство: Очевидно из первого признака параллельности прямых.
Теорема 9. Если при пересечении двух прямых а и b третей прямой с сумма внешних односторонних углов равна 180 градусам (одна пара), то такие прямые а и b являются параллельными
Доказательство: Очевидно из первого признака параллельности прямых.
Теорема 10. Если при пересечении двух прямых а и b третей прямой с соответственные углы равны (одна пара), то такие прямые а и b являются параллельными
Доказательство: Очевидно из первого признака параллельности прямых.
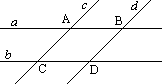
Доказательство: Пусть прямые a и b параллельны прямой c. Допустим, что прямые a и b не па-раллельны. Тогда либо прямые a и b совпадают, что противоречит условию, либо пересекаются в не-которой точке S. Тогда через точку S проходит две прямые — a и b, параллельные прямой c, что противоречит IX аксиоме. Значит, исходное предположение не верно. Теорема доказана.
Теорема 11.1. Если параллельно одной из двух параллельных прямых провести третью прямую, вторая из этих прямых либо параллельна третьей, либо совпадает с ней.
Доказательство: Очевидно из теоремы 11 параллельности прямых.
Теорема 12. Если прямая пересекает одну из параллельных прямых, то она пересекает и вторую.
Теорема 13. Отрезки параллельных прямых, заключенные между некой (иной) парой параллельных прямых, равны.
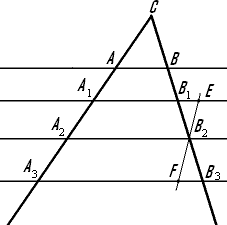
Теорема 14. (Теорема Фалеса) Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне.
Доказательство: Пусть A1, A2, A3 — точки пересечения параллельных прямых с одной из сторон угла, и точка A2 лежит между точками A1 и A3. Пусть B1, B2, B3 — соответствующие точки пересечения этих прямых с другой стороной угла. Докажем, что если A1A2 = A2A3, то B1B2 = B2B3. Проведем через точку B2 прямую EF, параллельную прямой A1A3. Треугольники EB2B1 и FB2B3 равны по второму признаку равенства треугольников. У них стороны EB2 и FA2 равны по условию, углы B1B2E и B3B2F равны как вертикальные, а углы B1EB2 и B2FB3 равны как внутренние накрест лежащие при секущей EF. Значит, B1B2 = B2B3. Что и требовалось доказать.
Теорема 14.1.. Параллельные прямые, пересекая стороны угла, отсекают пропорциональные отрезки.
Доказательство: Действительно, внутренние накрест лежащие углы равны 90°. Следовательно, по первому признаку параллельных прямых, эти прямые параллельны.
Теорема 16. Если прямая перпендикулярна одной из параллельных прямых, то она перпендикулярна и второй.
Доказательство: Очевидно из теоремы 15.
Видео:Перпендикулярность прямой и плоскости. 10 класс.Скачать

Перпендикулярные прямые в геометрии с примерами
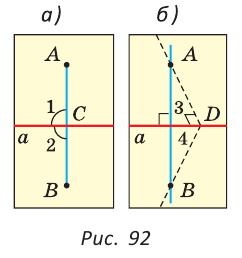
Определение: Две прямые называются перпендикулярными, если они пересекаются под прямым углом.
При пересечении двух перпендикулярных прямых образуются 4 прямых угла.
Отрезки и лучи называются перпендикулярными, если они лежат на перпендикулярных прямых. На рисунке 87 прямые
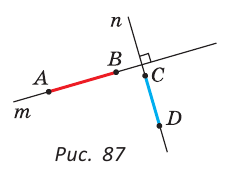
Определение. Перпендикуляром к данной прямой называется отрезок, который лежит на прямой, перпендикулярной данной, один из концов которого (основание перпендикуляра) является точкой пересечения этих прямых.
Прямая 

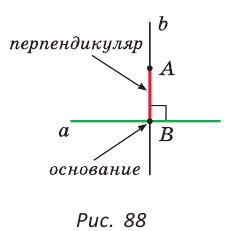
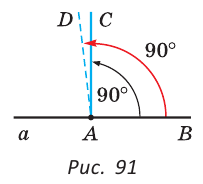
Если из точки М, которая не лежит на прямой 





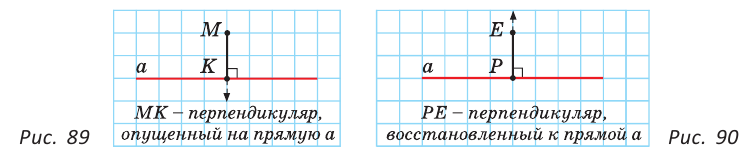
Теорема. Через точку, лежащую на данной прямой, можно провести прямую, перпендикулярную этой прямой, и только одну.
Дано: прямая 

Доказать: через точку А можно провести прямую, перпендикулярную прямой 
Доказательство:
По аксиоме откладывания углов от луча АВ в данную полуплоскость можно отложить угол CAB, равный 90°, и притом только один. Тогда прямая АС перпендикулярна прямой 

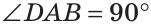
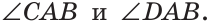

Теорема. Через точку, не лежащую на данной прямой, можно провести прямую, перпендикулярную этой прямой, и притом только одну.
Дано: прямая 
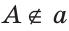
Доказать: через точку А можно провести прямую, перпендикулярную прямой 
Доказательство:
1) В начале докажем, что через точку А можно провести прямую, перпендикулярную прямой 


2) Теперь докажем, что АВ — единственная прямая, проходящая через точку А и перпендикулярная прямой 

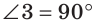
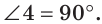

Из двух последних теорем следует, что на плоскости через любую точку можно провести прямую, перпендикулярную данной прямой, и притом только одну.
Теорема (о двух прямых, перпендикулярных третьей). На плоскости две прямые, перпендикулярные третьей, параллельны между собой.
Дано: 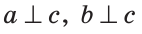
Доказать:
Доказательство:
Если предположить, что прямые 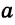
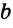
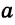
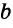
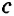
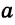
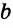
Теорема, обратная данной
Формулировка теоремы, как правило, состоит из двух частей: того, что дано, и того, что нужно доказать. Первая часть называется условием теоремы, вторая — заключением. Часто теорему формулируют в форме: «Если . (условие теоремы), то . (заключение теоремы)». Например, теорему о свойстве смежных углов можно сформулировать так: «Если углы смежные, то сумма этих двух углов равна 180°». «Углы смежные» — это условие теоремы, «сумма этих двух углов равна 180°» — заключение.
Если поменять условие и заключение теоремы местами, то получим утверждение, обратное данному. Для указанной выше теоремы получаем: «Если сумма двух углов равна 180°, то эти углы смежные». Но это утверждение неверно, поскольку можно привести пример двух углов, например, равных 60° и 120°, сумма которых 180°, но которые не являются смежными. Значит, приведенное утверждение не является теоремой.
Если же верно и обратное утверждение, то оно называется теоремой, обратной данной. Например, известна теорема: «Если сумма цифр числа делится на 3, то и число делится на 3» — и ей обратная: «Если число делится на 3, то и сумма цифр числа делится на 3».
Иногда прямую и обратную теоремы объединяют, употребляя при этом выражение «тогда и только тогда». Объединим вышеуказанные теоремы: «Число делится на 3 тогда и только тогда, когда сумма его цифр делится на 3».
Геометрия 3D
Пусть в пространстве прямая 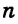
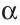
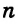
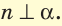
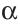
Чтобы прямая 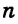
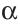
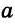
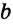
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Признаки равенства треугольников
- Признаки равенства прямоугольных треугольников
- Соотношения в прямоугольном треугольнике
- Сумма углов треугольника
- Расстояние между параллельными прямыми
- Задачи на построение циркулем и линейкой
- Задачи на построение по геометрии
- Угол — определение, виды, как обозначают с примерами
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Теорема о двух перпендикулярах к одной прямойСкачать

Стереометрия. Страница 3
|
| |||||||||||
| 1 2 3 4 5 6 7 8 | |||||||||||
 | |||||||||||
 Рис. 1 Перпендикулярность прямых в пространстве. Видео:Параллельность прямой и плоскости. 10 класс.Скачать  2.Признак перпендикулярности прямой и плоскостиТеорема. Прямая, перпендикулярная двум пересекающимся прямым на плоскости, перпендикулярна данной плоскости. Доказательство. Пусть прямые k и b две пересекающиеся прямые на плоскости α. Прямая а перпендикулярна прямым k и b. Доказать, что прямая а перпендикулярна плоскости α. (Рис.2) Проведем произвольную прямую х от точки А и прямую АВ, которая пересечет прямые k и b в точках К и В на плоскости α. Отложим на прямой а два равных отрезка в разные стороны АА’ и AA». Тогда треугольники АА’K и AA»K будут равны по двум сторонам и углу между ними. Так же как и треугольники АА’В и AA»В. Отсюда следует, что треугольники А’BK и А»BK равны по третьему признаку равенства треугольников. И следовательно, треугольники А’BE и A»BE равны, т.к. одна сторона у них общая ВЕ, стороны А’B и А»B равны из предыдущих рассуждений. Углы между этими сторонами также равны. Следовательно мы приходим к выводу, что треугольники А’AE и A»AE равны по трем сторонам. АЕ является медианой, биссектрисой и высотой, так как стороны А’Е и A»Е у них равные. И следовательно, угол между сторонами АА’ и АЕ равен 90°. Это значит, что прямая а перпендикулярна плоскости α. Рис.2 Признак перпендикулярности прямой и плоскости Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать  3. Теорема о трех перпендикулярахТеорема: если прямая, проведенная на плоскости и проходящая через основание наклонной, перпендикулярна ее проекции, то она перпендикулярна и наклонной. Доказательство. Пусть прямая СВ перпендикулярна плоскости α. АС — наклонная. Прямая а — прямая, проходящая через основание наклонной на плоскости α. (Рис.3) Проведем прямую через основание наклонной AD и параллельную прямой СВ. Тогда прямая AD также перпендикулярна плоскости α и соответственно прямой а. Проведем плоскость β через прямые АD и CB. Тогда, если прямая а перпендикулярна проекции наклонной АВ, то она перпендикулярна плоскости β. А следовательно, любой прямой в этой плоскости, т.е. самой наклонной АС. Следует отметить, что верно и обратное утверждение. Если прямая, проведенная на плоскости через основание наклонной ей перпендикулярна, то она перпендикулярна и проекции наклонной на эту плоскость. Рис. 3 Теорема отрех перпендикулярах. 4. Признак перпендикулярности плоскостей Теорема: Две пересекающиеся плоскости называются перпендикулярными, если третья плоскость перпендикулярна их прямой пересечения и пересекает их по перпендикулярным прямым. Пусть даны две плоскости α и β, которые пересекаются по прямой с (Рис.4). Проведем плоскость γ, которая пересекает плоскости α и β по прямым а и b. Плоскость γ перпендикулярна прямой с. Прямые а и b также перпендикулярны прямой с. Следовательно плоскости α и β перпендикулярны. Если взять другую плоскость, параллельную плоскости γ, например плоскость γ’, которая пересекает прямую с под прямым углом, она пересечет плоскости α и β по прямым a’ и b’, которые будут параллельны прямым а и b. По теореме о перпендикулярности прямых в пространстве прямые a’ и b’ также будут перпендикулярны, как и прямые а и b. Что и требовалось доказать. Рис. 4 Признак перпендикулярности плоскостей. Теорема: Если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны. Пусть α — плоскость. Прямая с перпендикулярна плоскости α. Точка А — точка пересечения прямой с и плоскости α (Рис.4.1). Проведем через прямую с плоскость β, которая будет пересекать плоскость α по прямой а. Необходимо доказать, что плоскости α и β перпендикулярны. Проведем через точку А на плоскости α прямую b, перпендикулярную прямой а. Через прямые b и с проведем плоскость γ. Она перпендикулярна прямой а, так как прямая а перпендикулярна двум прямым b и с. Тогда плоскость β пересекает две плоскости α и γ по двум перпендикулярным прямым а и с. И пересекает прямую пересечения b под прямым углом. Следовательно плоскости α и β перпендикулярны. Рис. 4.1 Перпендикулярность плоскостей. Видео:Перпендикуляр и наклонная в пространстве. 10 класс.Скачать  5. Расстояние между скрещивающимися прямымиТеорема. Две скрещивающиеся прямые имеют только один общий перпендикуляр, который также является перпендикуляром между параллельными плоскостями, проведенными через эти прямые. Доказательство. Пусть а и b две скрещивающиеся прямые (Рис.5). Проведем через них две плоскости α и β, параллельные друг другу. А от прямой а проведем перпендикуляры на плоскость β. Таким образом, получим плоскость γ, которая перпендикулярна обоим плоскостям α и β и пересекает плоскость β по прямой a’. Прямые а и a’ параллельны. Прямая a’ пересекает прямую b в точке А. Следовательно, один из перпендикуляров, проведенных от каждой точки прямой а на плоскость β, т.е. отрезок АВ и есть общий перпендикуляр между прямыми а и b. Допустим, что существует еще один общий перпендикуляр между прямыми а и b это CD. Тогда два перпендикуляра пересекают прямые а и b в точках А,В,С,D, которые в свою очередь параллельны между собой. Следовательно через них можно провести плоскость. А в этой плоскости лежат и две прямые а и b, которые также будут параллельны между собой. А это противоречит условию, т.к. прямые а и b являются скрещивающимися. Следовательно у двух скрещивающихся прямых может быть только один общий перпендикуляр. Отсюда следует, что расстояние между двумя скрещивающимися прямыми равно длине их общего перпендикуляра. Рис. 5 Расстояние между скрещивающимися прямыми. | |||||||||||
 | |||||||||||