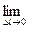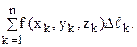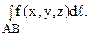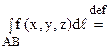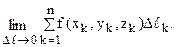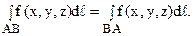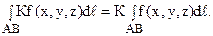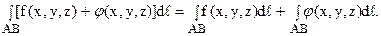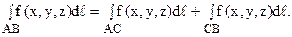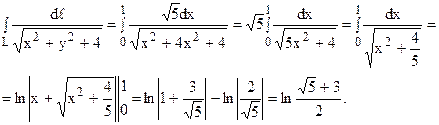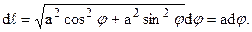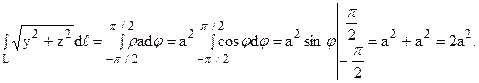Дуга развертки окружности x a cost tsint (7 видео)

Вычисление длины дуги плоской кривой

Используя теорему Пифагора и кусочно-линейную аппроксимацию плоской кривой, получим

I = Jdl = J7( dx ) 2 + (dy) 2 = f V 1 + 1 f ‘(x)] 2 dx

Рисунок 10 — Длина дуги плоской кривой

Длина дуги кривой определяется по формулам:

для кривой, заданной в декартовой системе координат:

для кривой, заданной в параметрической форме:

Р/ а-х-0′ 1=JVOO2 +(у’)2

для кривой, заданной в полярных координатах:

r=r(p), а 2 + r 2 d^. (22)

Последнее выражение получено посредством разложения вектора г ( ) на проекции х = г cos (р, у = г sin (р, связывающих полярные и декартовы координаты. Если параметром считать угол (р, то кривая АВ задана параметрически. Воспользовавшись формулой (21), получим

=r^cos^-rsin^; у^ =r^sin^ + rcos^;

( М + W = ( г ? cos ^ “ г sin + sin + г cos ^) = (г; ) + г 2 .

В результате получаем (22).

Пример 1. Вычислить длину дуги кривой у = In х содержащейся между точками, для которых х =

Воспользуемся формулой (20).

Здесь а = л/8; b = >/15 ; f(x) = lnx;

+ l = t 2 ; xdx = tdt

= 4 +-In — 3—In—= l + -ln = 1 +—In—.

2 5 2 4 2 5-2 2 5

Пример 2. Вычислить длину дуги кривой, заданную параметрически

х = 4(cost + tsint)

0 2 cos 2 1 + 16t 2 sin 2 tdt = j 4tdt = 2t 2

Пример 3. Вычислить длину дуги кривой, заданную уравнением в полярных

координатах р = 2е 4 ^ /3 ; -л / 2 2 + arcsin х, 0 I г

S. = 2л——1 = 2/rR 1, (23)

где R_cp — среднее значение радиусов R и г; 1 — образующая.

Найдем дифференциал площади ds усеченного конуса с образующей dl, и радиусами оснований у и у + dy. Площадь его боковой поверхности равна

ds = тг( у + у + dy) • dl = 2тг ydl + Trdydl.

Отбрасывая произведение dydl как бесконечно малую высшего порядка, чем ds, получаем ds = 2^ydl, или, так как dl = д^1 + (у’) 2 dx, то ds = 2яу^1 + (у’) 2 dx.

Интегрируя полученное равенство в пределах от X = а до х = b, получаем искомую площадь поверхности вращения ь .

s x =2л-/у7 1 + (Ух) 2 — ( 24 )

Если кривая задана параметрическими уравнениями, то по аналогии с (21)

Если кривая задана в полярной системе координат, то по аналогии с (22)

При вращении кривой вокруг оси OY

Пример 1. Найти площадь поверхности шара радиуса R.

Поверхность шара образована вращением полуокружности у = —R 1 1 1

-cos — sin — dt =

. о 2Г . 2 t . t , dt=8^a sin — sin—dt =

о 2 2

u = cos—; t=0, u=l; t=7T, u=0

, It,

du = —sin—dt;

2 2
-16?ra2 u — ——

1 32 2 о 64 2

2 3 3

Пример 3. Найти площадь тора, образующегося при вращении окружности г = sin ф вокруг оси Ох.

S_x = 2л jsinф • sin ^/sin ф + cos 1 ф&ф = л j(l — cos 2^)d^ = л 1 .

Задания для решения в аудитории:

1. Найти площадь поверхности, полученной вращением вокруг оси Ох дуги параболы у = 2л/х, 0
?x 5 >/x 2 -l yi + cosx • 2
4) Вычислить площадь фигуры, ограниченной линиями: у 2 =16-8х и у 2 =24х+48.

5) Вычислить длину всей линии: S = sin —.
6) Вычислить объём тела, полученного от вращения вокруг оси абсцисс фигуры, ограничен

ной фигуры, ограниченной осью ОХ, прямой х = тс и аркой циклоиды

Вариант 3.

—ах а >0
2 х
4) Вычислить площадь фигуры, ограниченной линиями: у 2 =х 2 -3х и Зх+у-4=0.

[х = R(cost + tsint)

5) ВЫЧИСЛИТЬ ДЛИНУ ЛИНИИ: 3 _« оо

1). f х 2 х/1 — x 2 dx 2). Г—. 3). f х 2 е” х dx

4) .Фигура ограничена линией S = 4cos3^. Вычислить площадь той её части, которая рас

положена вне круга S = 2.

5) Вычислить длину дуги кривой у = -уДх + 1) 3 (—1 2 = 2рхи х=п (р>0,п>0).

Содержание

Криволинейные интегралы первого рода (по длине дуги) – КИПР.
Дуга развертки окружности x a cost tsint
Контакты
🔍 Видео

Видео:Определение центра дуги окружности, построение окружности по 3 точкамСкачать

Криволинейные интегралы первого рода (по длине дуги) – КИПР.

Пусть в пространстве Oxyz задана непрерывная спрямляемая кривая АВ, в точках которой определена произвольная функция f(x, y, z). Проделаем 5 операций:

1. Разобьем кривую АВ на n частей точками М₁, М₂, ….М_n-1, следующими друг за другом в направлении от А к В (для определенности). Точку А обозначим через М₀, точку В через М_n. Длины дуг М_k-1 М_k (k = 1, 2,…, n) обозначим, соответственно, через . Наибольшую из величин
(k = 1, …, n) обозначим через 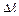и назовем рангом (шагом) дробления кривой АВ.

2. На каждой дуге М_k-1 М_k (k = 1, 2, …, n) выберем произвольным образом по точке N_k(x_k; y_k; z_k) и вычислим в них значения функции
f(x, y, z), т.е. найдем числа f(x_k, y_k, z_k).

3. Вычислим произведения f(x_k, y_k, z_k) (k = 1, 2, …, n).

4. Найдем сумму 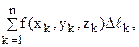которую называют интегральной суммой для функции f(x, y, z) на кривой АВ, отвечающей данному разбиению (дроблению) АВ на части и выбору точек N_k (x_k; y_k; z_k).

5. Измельчая дробление, ищем предел

( 1)

Если существует конечный предел ( 1), не зависящий ни от способа дробления кривой АВ на части, ни от выбора точек N_k(x_k; y_k; z_k) (k = 1, 2, …, n), то этот предел называют криволинейным интегралом первого рода (по длине дуги) от функции f(x, y, z) по дуге АВ и обозначают символом:

При этом функцию f(x, y, z) называют подынтегральной функцией, кривую АВ – линией (кривой, контуром) интегрирования, точку А – начальной, а точку В – конечной точками интегрирования (тем самым устанавливается направление интегрирования).

Таким образом, по определению

( 2)

Перечислим простейшие свойства криволинейного интеграла первого рода (в основном аналогичные свойствам определенного интеграла):

1. Значение криволинейного интеграла первого рода не зависит от направления на кривой:

2. Постоянный множитель в подынтегральной функции можно выносить за знак криволинейного интеграла:

3. Криволинейный интеграл первого рода от суммы двух функций равен сумме интегралов от этих функций:

4. Если кривая АВ разбита точкой С на две части АС и СВ, то криволинейный интеграл по всей кривой АВ равен сумме интегралов по ее частям:

5. Если в каждой точке кривой АВ функции f(x, y, z) и j(x, y, z) удовлетворяют неравенству f(x, y, z)

Пример 1.

Вычислить 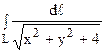, где L – отрезок прямой, соединяющий точки О(0;0) и А(1;2).

Запишем уравнение прямой L: y = 2x (явное задание). Для данной линии При движении от О к А х меняется от 0 до 1. По формуле ( 5) имеем:

у = 2х

Пример 2.

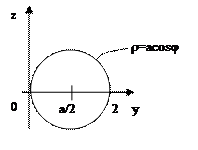
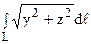
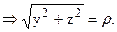
Дуга развертки окружности x a cost tsint

Вычислить , где L – контур окружности y 2 + z 2 = ay (a > 0).

Введем полярные координаты: y = rcosj, z = rsinj .

Уравнение окружности принимает вид: r 2 = arcosj или r = acosj.

Тогда r’ = -asinj и

Т. к. окружность расположена в той части плоскости yOz, где y > 0, то угол j меняется от -p/2 до p/2. По формуле ( 7) имеем:

Пример 3.

Вычислить 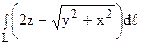, где L – дуга кривой, заданной параметрически:
x = tcost, y = tsint, z = t (0 2 , 0 3 = 3a 2 y, 2xz = a 2 , заключенной между плоскостями y = 9a,
y = a/3.

Длину дуги L можно записать в виде : .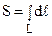

Приняв за параметр координату х, уравнения данной линии можно представить в параметрическом виде: x = t, y = t 3 /3a 2 , z = a 2 /2t. Значения параметра, соответствующие концам рассматриваемой дуги, вычисляются по формуле: 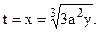Таким образом,
t₁ = a, t₂ = 3a.