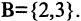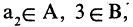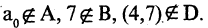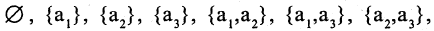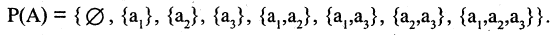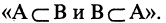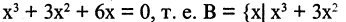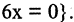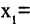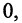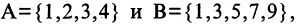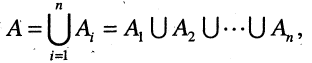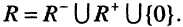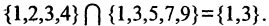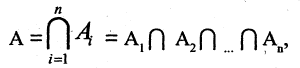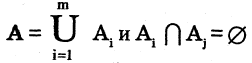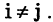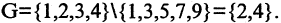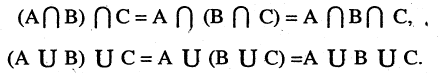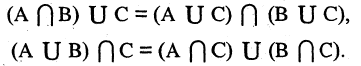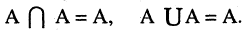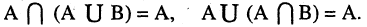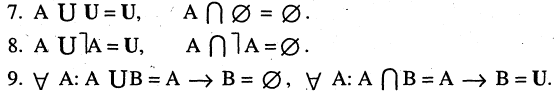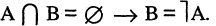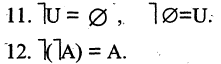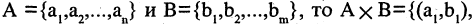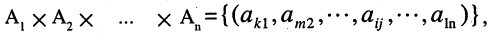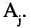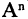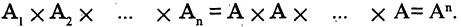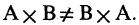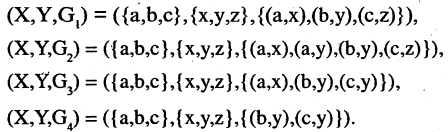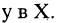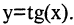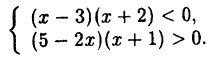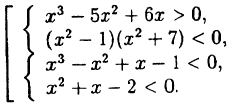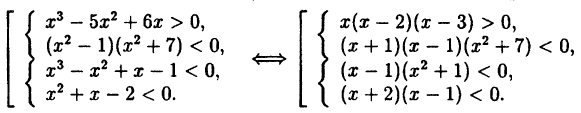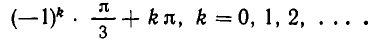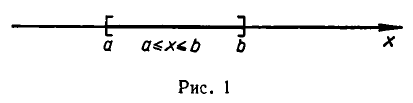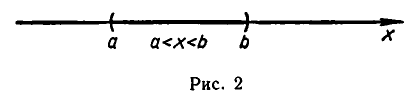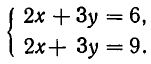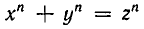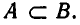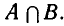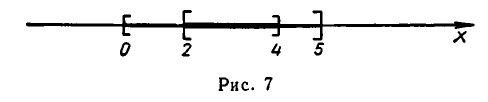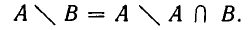Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
«Актуальность создания школьных служб примирения/медиации в образовательных организациях»
Свидетельство и скидка на обучение каждому участнику
Практическая работа №1
Тема: «Выполнение операций над множествами»
Цель: развитие практических навыков задания множеств, выполнения операций над множествами.
Время выполнения : 90 минут.
1. Найдите объединение, пересечение, разность множеств А и В , если:
а) А = ] 

2. (Устно) Найдите дополнение в множестве всех треугольников к множеству:
а) всех равносторонних треугольников;
б) всех равнобедренных треугольников;
в) всех прямоугольных треугольников.
а) А 

б) ( С 


в) А 


г) А 

д) А 

4.(Устно)Приведите примеры множеств, составленных из объектов следующих видов:
а) неодушевленных предметов;
г) геометрических фигур;
д) населенных пунктов;
ж) политических деятелей.
Пусть А – множество корней уравнения

а) А
2. Перечислите элементы каждого из множеств:
а) А = < x : x 
б) В = < х : x 
в) С = < х : x 
3.Даны множества: А= 
4.Даны два множества: А – множество стран и В – множество материков. Задайте соответствие между этими множествами с помощью стрелок. А= 

Пусть А – множество корней уравнения

а) А
2. Перечислите элементы каждого из множеств:
а) А = < х : x 
б) В = < х : x 
в) С = < х : x 
3.Даны множества: А= 
4.Даны два множества: А – множество месяцев года и В – множество времён года. Задайте соответствие между этими множествами с помощью стрелок.
Пусть А – множество корней уравнения

а) А
2. Перечислите элементы каждого из множеств:
а) А = < х: x 
б) В = < х : x 
в) С = < х : x 
3.Даны множества: А= 
4.Даны два множества: А – множество стран и В – множество материков. Задайте соответствие между этими множествами с помощью стрелок. А= 

Пусть А – множество корней уравнения

а) А
2. Перечислите элементы каждого из множеств:
а) А = < х : х 
б) В = < х : х 
в) С = < х : х 
3.Даны множества: А= 
4. Даны два множества: А – множество месяцев года и В – множество времён года. Задайте соответствие между этими множествами с помощью стрелок.
1. Назовите элементы, принадлежащие множеству:
а) студентов вашей группы;
б) предметов, изучаемых в I семестре вашей специальности;
в) всех частей света;
г) субъектов федерации, входящих в Российскую Федерацию.
2. Пусть А – множество многоугольников. Принадлежат ли этому множеству:
3.Запишите перечислением элементов следующие множества:
а) А – множество нечетных чисел на отрезке [1; 15];
б) В – множество натуральных чисел, меньших 8;
в) С – множество натуральных чисел, больших 10, но меньших 12;
г) D – множество двузначных чисел, делящихся на 10;
д) Е – множество натуральных делителей числа 18;
е) F – множество чисел, модуль которых равен 
4.На факультете филологии и журналистики учатся студенты, получающие стипендию, и студенты, не получающие стипендию. Пусть А – множество всех студентов факультета; В – множество студентов факультета, получающих стипендию.
Укажите, что собой представляет объединение , пересечение и разность множеств А и В .
Для отчёта представить:
Решение индивидуального задания.
Письменные ответы на контрольные вопросы.
«5» — выполнено 90-100% всех заданий;
«4» — выполнено 70-90% всех заданий;
«3» — выполнено 50-70% всех заданий;
«2» — выполнено менее 50% всех заданий.
Самые массовые международные дистанционные
Школьные Инфоконкурсы 2022
33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»
- Множество в математике с примерами решения и образцами выполнения
- Операции над множествами
- Равенство множеств
- Объединение (сумма) множеств
- Пересечение (умножение) множеств
- Разность двух множеств
- Прямое произведение множеств
- Понятие соответствия
- Мощность множества
- Множества — основные понятия
- Операции над множествами
- Кванторы общности и существования
- Множество N натуральных чисел
- Множество Z целых чисел
- Множество Q рациональных чисел
- Числовая ось
- Числовые промежутки
- Примеры с решением на тему: «Множества«
- Множества
- Числовые множества
- Пустое множество
- Подмножество
- Пересечение множеств
- Сложение множеств
- Разбиение множеств
- Вычитание множеств
- Отображение множеств
- Краткие исторические сведения
- Дополнение к различным типам множеств
- Дополнение к множеству треугольников
- 📺 Видео
Видео:3.5 Дополнение множестваСкачать

Множество в математике с примерами решения и образцами выполнения
Математика — это точная абстрактная наука, оперирующая своими специальными понятиями, структурами и символами. Основными методами в математических исследованиях являются строгие логические рассуждения, а объектами изучения — математические модели. Но абстрактность математики не означает ее отрыв от реальной жизни. Реальные задачи описываются в математических терминах, как правило в безразмерном виде. Это есть так называемая
математическая модель явления. При решении уже поставленной математической задачи используются абстрактные математические методы.
Одна и та же математическая модель может описывать свойства различных реальных явлений. Само реальное явление рассматривается вновь после решения математической задачи и ее анализа, на основании которого могут быть сделаны выводы
не только о состоянии явления, но и о его развитии. В этом смысле без математики нет науки. Еще великий Леонардо да Винчи писал: «Никакой достоверности нет в науках там, где нельзя применить ни одну из математических наук, ив том, что не имеет связи с математикой.» И еще: » Ни одно человеческое исследование не может называться истинной наукой, если оно не прошло через математические доказательства.»
Математические методы играют огромную роль в образовании современного высококвалифицированного специалиста в технических областях, предоставляя ему аппарат исследования, дисциплинируя, приучая к строгим логическим рассуждениям.
Поскольку язык и методы математики широко используются при современном преподавании всех естественно-научных и технических дисциплин, математика изучается с первого семестра в любом высшем техническом учебном заведении, и на нее выделяется значительная часть бюджета времени студента.
Под множеством понимают любой набор определенных и различимых между собой объектов, рассматриваемых как единое целое. Это высказывание не является определением, поскольку слово « множество» заменено словом «набор». Близкими к понятию «множество» являются понятия: собрание, совокупность, комплекс, система и т. п. Вместе с тем здесь имеется три важных момента.
Объекты, входящие во множество, определенные (т. е. для каждого объекта можно однозначно сказать, принадлежит ли он данному множеству или нет), различимы между собой (во множестве не может быть двух или более одинаковых объектов) и все объекты, входящие во множество, мыслятся как единое целое (все объекты рассматриваются в совокупности, а от свойств отдельных объектов абстрагируются).
Множества обозначают прописными буквами латинского алфавита. Объекты, входящие во множество, называют элементами и их обозначают строчными буквами. Множество, состоящее из конечного числа элементов, называется конечным, в противном случае множество называется бесконечным.
Множество может быть задано при помощи правила, позволяющего определить, является ли данный объект элементом множества или нет. В записи правило, задающее множество, отделено вертикальной чертой. Например, пусть множество В есть множество решений уравнения 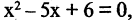
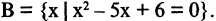
Конечное множество может быть задано перечислением входящих в него и разделенных запятой элементов, например, 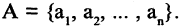
мента, называется пустым и обозначается символом 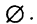
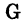
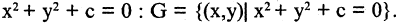
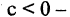
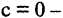
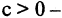
Для указания того факта, что объект принадлежит данному множеству, используют знак 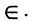
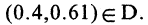
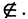
Множество В называется подмножеством множества А, если каждый элемент В одновременно является элементом множества А. Это записывается так:
Пример:
Пусть заданы множества 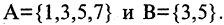
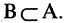
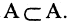
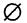
Пример:
Если 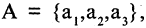
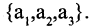
Если конечное множество А состоит из п элементов, то оно имеет ровно 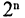
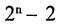
Замечание. Не следует путать символы 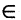

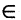

Зафиксированное каким-либо образом множество объектов, допустимых при данном рассмотрении, называют базовым или универсумом. Базовое множество обозначают буквой 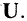
Видео:2.6 Дополнение множества | Константин Правдин | ИТМОСкачать

Операции над множествами
Множества можно складывать и вычитать, то есть совершать операции.
Равенство множеств
Множества А и В считаются равными, если они состоят из одних и тех же элементов. Равенство множеств обозначают так: А=В. Если множества не равны, то пишут: А 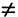
Пример. Доказать, что множество 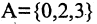
Для доказательства решим уравнение. Получим: 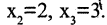
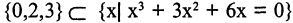
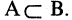
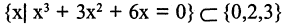
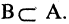
Объединение (сумма) множеств
Объединением множеств А и В называется такое множество С, каждый элемент которого содержится хотя бы в одном из множеств А или В. Обозначается: 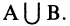
Можно рассматривать объединение 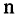
при этом в А входят все элементы, которые входят хотя бы в одно из множеств 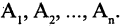
ствительных чисел 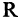
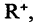
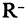
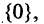
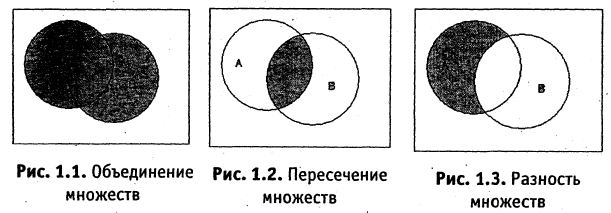
Для наглядного представления соотношений между несколькими подмножествами какого-либо универсума часто используются круги Эйлера или диаграммы Венна. Универсум представляется множеством всех точек некоторого прямоугольника, а его подмножества — соответствующими кругами. Операция объединения и другие операции иллюстрируются кругами Эйлера представленными на рис. 1.1-1.5.
Пересечение (умножение) множеств
Пересечением множеств А и В называется множество D, составленное из общих для множеств А и В элементов. Обозначение: 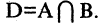
Можно рассматривать пересечение 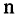
при этом в А входят только те элементы, которые входят во все множества 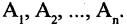
Пусть есть некоторое множество А. Говорят, что задано разбиение множества А на классы 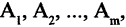
для всех 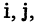
Классы — это такие подмножества разбиваемого множества, которые не имеют общих элементов, а их объединение образует исходное множество А. Следовательно, каждый элемент множества А входит в один и только в один класс.
Видео:Множество. Элементы множества. 5 класс.Скачать

Разность двух множеств
Разностью двух множеств А и В называется множество G, содержащее лишь те элементы из А, которые не входят в В. Обозначение: 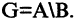
Если В — подмножество 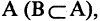
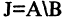
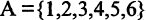
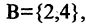
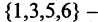
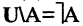
Пример. Пусть 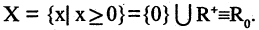
Тогда 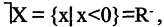
Операции над множествами подчиняются определенным законам. Перечислим их.
1.Коммутативный или переместительный закон
2.Ассоциативный или сочетательный закон
Так как порядок выполнения операций несущественен, то скобки в записи опускают.
3.Дистрибутивный или распределительный закон:
6.Закон двойственности де Моргана:
10.Если 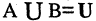
Из законов (1-12) следует принцип двойственности: всякое равенство, тождественно выполняемое в теории множеств, переходит также в тождественно выполняющееся равенство при замене знака объединения 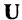
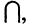
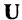
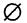
Видео:Подмножество. Операции над множествами (пересечение, объединение множеств) – 8 класс алгебраСкачать

Прямое произведение множеств
Кортежем называют любую выделенную упорядоченную совокупность объектов (элементов кортежа). Синонимами понятия «кортеж» являются: упорядоченная система, упорядоченная совокупность, вектор, упорядоченный набор, «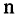
одинаковую длину, и все их соответствующие компоненты совпадают.
Элементы, составляющие кортеж, называются компонентами, которые в силу упорядоченности имеют номер: первый компонент, второй компонент, … 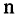
Примеры кортежей: 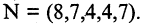
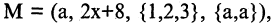
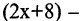
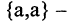
Прямым произведением двух множеств А и В (обозначается 
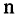
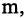
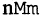
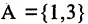
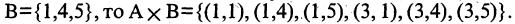
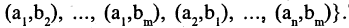
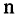
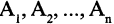
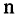
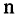
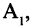
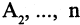
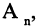
где 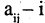
Если все множества 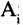
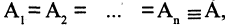
Например: пусть R — множество действительных чисел, тогда 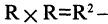
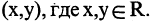
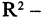
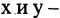
каждый его элемент является упорядоченной парой, следовательно, любое подмножество множества 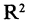
Проекцией кортежа 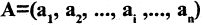
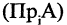
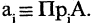
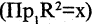
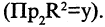
Пример:
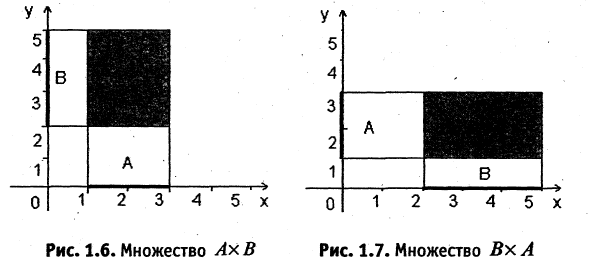
Пусть А — отрезок [1,3], В — отрезок [2,5]. Тогда 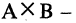
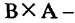
Пример:
Пусть А — множество, элементами которого являются буквы, цифры и все знаки операций и препинания. Такое множество называют алфавитом. Тогда 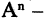
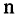
Природа компонентов прямого произведения обычно отличается от природы элементов сомножителей. Например, пусть Q — множество участников шахматного турнира, тогда 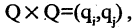
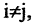
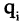
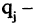
Видео:9 класс, 2 урок, Множества и операции над нимиСкачать

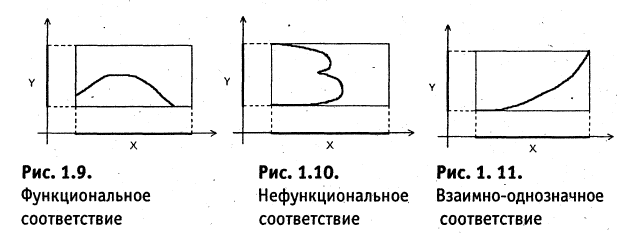
Понятие соответствия
Пусть заданы два множества 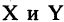
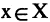
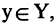
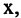
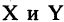
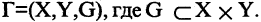
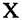
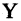
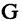
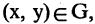
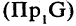
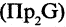
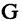
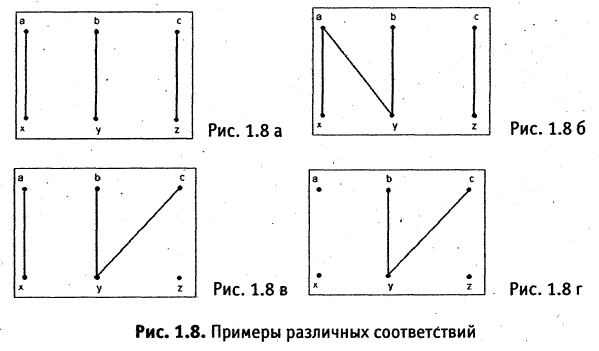
Два соответствия равны тогда и только тогда, когда равны их области отправления, области прибытия и графики. Пример. Заданы четыре разных соответствия, имеющие одинаковые области отправления и прибытия:
На рис. 1.8а, 1.86, 1.8в, и 1.8г. различия этих соответствий видны достаточно наглядно.
В соответствии 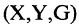
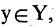
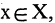
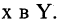
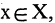
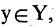
Соответствие называется всюду определенным, если множество 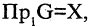
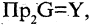
Соответствие 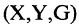
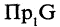
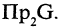
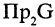
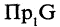
Соответствие между 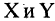
Пусть 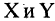
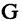
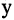
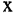
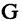
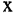
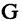
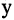
Видео:Множества и операции над нимиСкачать

Мощность множества
Мощность множества характеризует количество элементов этого множества. Множества равномощны, если между их элементами можно установить взаимно-однозначное соответствие. Число элементов в конечном множестве А называется кардинальным числом и обозначается |А|. Подсчет элементов конечного множества заключается в установлении взаимно-однозначного соответствия между этими элементами и конечной последовательностью натуральных чисел.
Множество называется бесконечным, если оно равномощно хотя бы одному из его собственных подмножеств. Бесконечное множество А называется счетным, если оно равномощно множеству всех натуральных чисел N. Примеры счетных множеств: множество целых чисел, четных чисел, рациональных чисел. Счетное множество образуется при объединении счетного множества конечных множеств (например, множество слов в любом конечном алфавите) и т. д. Счетным будет и объединение счетного множества счетных множеств (множество всех векторов с натуральными компонентами). Множество А называется не более чем счетным, дискретным, если оно конечно (в частности, пусто) или счетно. Счетное множество среди бесконечных множеств имеет наименьшую мощность.
Рассмотрим все вещественные числа на отрезке 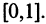
единичного отрезка числовой оси, имеет мощность континуума (непрерывное множество). Мощность множества континуума превышает мощность счетного множества. Любой конечный отрезок числовой оси равномощен единичному отрезку. Более того, любой конечный отрезок равномощен и всей числовой оси. Например, между отрезком 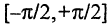
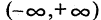
Множества наибольшей мощности не существует. Это следует из того, что мощность любого множества А всегда строго меньше мощности множества всех его подмножеств
Видео:A.2.8 Дополнение, вычитание и декартово произведение множествСкачать

Множества — основные понятия
Под множеством понимается совокупность каких-либо объектов, называемых элементами этого множества. Например, можно говорить о множестве студентов данного вуза, множестве учебников по математике, множестве треугольников, множестве действительных чисел и т. д. Множества, содержащие конечное число элементов, называются конечными (множество студентов, множество учебников). Множества с бесконечным числом элементов называются бесконечными (множество треугольников, множество действительных чисел).
Множество обычно обозначается заглавными латинскими буквами A, B, С, …, а их элементы — малыми а, b, с, ….
Утверждение ’’элемент х принадлежит множеству А” записывается так : «х ∈ А ”, а противоположное утверждение ” элемент х не принадлежит множеству А” записывается так : ”х ∉ А ”.
Определение:
Если все элементы множества А принадлежат также множеству В, то говорят, что ” А содержится в В” или: ” А является подмножеством В”, и записывают так: A ⊂ В.
Определение:
Два множества называются равными (совпадающими), если они состоят из одних и тех же элементов: A = B.
Пример:
Сформулируйте словами утверждение:
A=B⇔ A ⊂ B и B ⊂ A и докажите его.
Конечное множество можно задать перечислением его элементов. Так, запись A = означает, что множество А состоит из трех чисел 1,2,3. При этом порядок перечисления элементов не играет роли: = .
Бесконечное множество можно задать, написав условие, которое выполняется для всех элементов данного множества и не выполняется для других. Запись
В = <x | 1 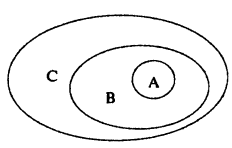
Определение:
Множество называется пустым, если оно не содержит ни одного элемента. Пустое множество обозначается символом ⊘.
Так, например, множество отрицательных натуральных чисел пусто.
Операции над множествами
Определение:
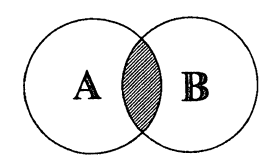
Пересечением множеств A и B называется множество С, состоящее из всех элементов, одновременно входящих и в А, и в В. Это записывается следующим образом: A ∩ В = С.
Иллюстрация пересечения двух множеств с помощью диаграмм Эйлера приведена на рис. 2, где множество C заштриховано.
Пример:
Если множество А есть интервал (1 ;5) а множество В есть интервал (2;7), то пересечение множеств A и B есть интервал (2;5).
Свойства операции пересечения множеств приведем без доказательств:
- A ∩ В = В ∩ А(коммутативность).
- A ∩ (В ∩ С) = (A ∩ В) ∩ C = A ∩ В ∩ С(ассоциативность).
- A ⊂ В ⟹ А ∩ В = А.
- A∩A= А.
- A ∩ ⊘ = ⊘
Определение:
Объединением множеств A и B называется множество С, состоящее из всех элементов, каждый из которых принадлежит хотя бы одному из данных множеств или А, или В, или A u B одновременно. Это обозначается следующим образом : A ∪ В = С.
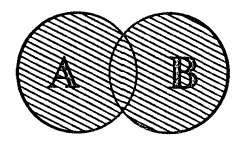
Иллюстрация объединения с использованием диаграмм Эйлера приведена на рис. 3, где множество C заштриховано.
Пример:
Если множество А есть отрезок [1;3], множество В есть отрезок [2;5], то A ∪ B есть отрезок B=[1;5].
Свойства операции объединения множеств приведем без доказательств:
1) A ∪ B=B ∪ A (коммутативность).
2) A ∪ (B∪C)=(A ∪ B) ∪ C=A ∪ B ∪ C (ассоциативность).
3) A∩(B∪C)=(A∩B) ∪ (A∩C) (дистрибутивность).
4) A ⊂ B ⇒A ∪ B=B.
5) A ∪ A=A.
6) A ∪ ⊘=A.
Определение:
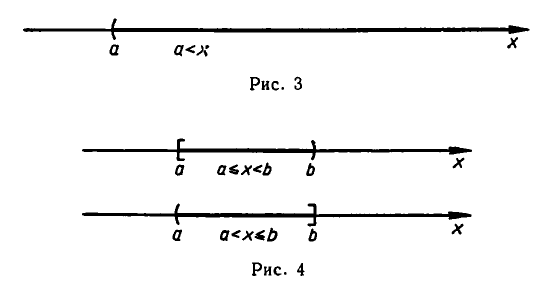
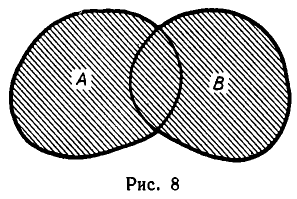
Разностью множеств А и В называется множество С, состоящее из всех элементов, принадлежащих множеству А, но не принадлежащих В. Разность A u B обозначается АВ и изображена штриховкой на рис. 4.
Операция вычитания множеств не коммутативна : A∖B≠B∖A.
Пример:
Если А = (1; 10), В = (3; 20), то АВ=(1;3], ВА =[10,20).
Кванторы общности и существования
При изложении материала мы будем использовать знак 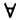
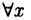
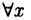
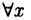
Обозначение Ǝх означает: ’’существует такое х, что …”, ”по крайней мере для одного х…”, запись Ǝх > 0 читается: ’’существует такое положительное число х, что…”, запись Ǝх₁ ,x₂ Є M означает: ’’существуют такие х₁ ,x₂ — элементы множества М, что …”.
Нам также неоднократно придется использовать символы ⇒ и ⇔.
Запись логического следования А ⇒ В означает, что если верно утверждение А, то верно и утверждение В, то-есть из А следует В.
Запись логической равносильности ⇔ означает, что из А следует В и наоборот, из В следует А.
Так, например, запись: 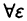
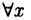
Любая теорема может быть сформулирована в виде: если выполняется условие А, то верно утверждение В. Будем называть это прямой теоремой и схематически запишем в виде:
Теорема:
В качестве примера приведем теорему, называемую достаточным условием экстремума непрерывной функции, изучаемую в курсе математики средней школы.
Теорема:
Если функция f непрерывна в точке а и производная f меняет знак при переходе через эту точку, то а является точкой экстремума функции f.
Условие А стоит после слова «если», утверждение В написано после
слова «то».
Определение:
А называется достаточным условием для
выполнения В. В свою очередь, В является необходимым условием для выполнения А.
Применительно к теореме 1.2 это выглядит следующим образом.
Достаточным условием для существования экстремума непрерывной функции f в точке а является изменение знака ее производной при переходе через эту точку.
Для лучшего усвоения введенных понятий рассмотрим очевидно справедливое утверждение не из области математики.
Теорема:
Если человек здоров, то у него есть голова.
Здесь здоровье является достаточным условием наличия у человека головы. Наоборот, наличие головы является необходимым условием здоровья. Подумайте, будет ли это условие достаточным для того, чтобы человек был здоров? Реально ли вообще сформулировать достаточное условие того, что человек здоров?
Обозначим А утверждение, заключающееся в отрицании утверждения А(читается «не А»). Если справедлива прямая теорема 1.1, то методом «от противного» легко можно доказать справедливость следующего утверждения, которое называется
«противоположная к обратной теорема»:
Теорема:
Доказательство:
Имеем А ⇒ В, нужно доказать, что В⇒ А Предположим противное: В ⇒ А, но в соответствии с теоремой 1.1 А ⇒ В. Полученное противоречие (В ⇒ В) доказывает теорему.
Аналогично можно доказать, что если справедлива теорема 1.4, то верна теорема 1.1, т. е. эти утверждения равносильны.
Для теоремы 1.2 противоположной к обратной будет теорема: ’’Если точка а не является точкой экстремума функции f ̕ непрерывной в этой точке, то производная f ̕ не меняет знак при переходе через эту точку”.
Для теоремы 1.3 противоположным к обратному будет утверждение: ’’Если у человека нет головы, то он не здоров”.
Проведите доказательство этого утверждения самостоятельно методом ”от противного».
Наряду с прямой теоремой 1.1 можно рассмотреть утверждение, называемое «обратной теоремой” :
Теорема:
Однако обратная теорема не всегда справедлива, если верна прямая. Так, например, для теоремы 1.3 обратное утверждение: «Если у человека есть голова, то он здоров”, очевидно, не верно.
Если все же теорема 1.5 справедлива, то методом «от противного” исходя из нее доказывается справедливость утверждения, называемого «противоположная теорема”:
Теорема:
Наоборот, из теоремы 1.6 вытекает справедливость теоремы 1.5, т.е. эти утверждения равносильны. Заметим, что из прямой теоремы 1.1 не обязательно следует справедливость противоположной теоремы 1.6.
Приведенные связи удобно запоминать, представляя себе следующий ’’логический квадрат» (рис. 5):
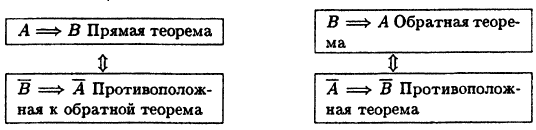
Если наряду с прямой теоремой выполняется также обратная теорема, то А является ’’необходимым и достаточным” условием для В. То же самое можно сказать про В по отношению к А.
Так, например, то, что треугольник прямоугольный, является необходимым и достаточным условием того, что квадрат одной из сторон равен сумме квадратов двух других.
Множество N натуральных чисел
Определение:
Числа 1,2,3,… называются натуральными.
Сумма и произведение натуральных чисел будет числом натуральным, а разность и частное — не всегда. При вычитании натуральных чисел может получится отрицательное число, а при делении — не целое. Например, при делении 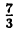
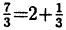
Приводя к общему знаменателю, получим равенство: 7 = 2 ∙ 3 + 1. В этих равенствах 7 называется делимым, 3 — делителем, 2 — целой частью и 1 — остатком (остаток всегда меньше делителя). Если остаток равен нулю, то говорят, что делимое делится на делитель, как, например, 6 делится на 3. Если натуральное число, большее единицы, делится только на 1 и на себя (что всегда справедливо), то оно называется простым. Простыми числами являются числа 2,3,5,7,11,13,17,19,23 и т. д. Любое натуральное число может быть представлено в виде произведения простых сомножителей. Например : 12 = 1 ∙ 2 2 3, 18 = 1 2 ∙ 3 3, 7 = 1 ∙ 7 и т. д.
Определение:
Наименьшим общим кратным двух данных натуральных чисел называется наименьшее из чисел, которые делятся на каждое из них.
Для любых двух натуральных чисел всегда найдется наименьшее общее кратное, поскольку их произведение всегда делится на каждое из двух данных.
Наименьшее общее кратное 12 и 18 равно 36. Для того чтобы найти наименьшее общее кратное двух чисел, нужно первое число помножить на простые множители, входящие в разложение второго числа и не входящие в разложение первого: 12 ∙ 3 = 36.
Определение:
Наибольшим общим делителем двух данных натуральных чисел называется наибольшее из чисел, на которые делится каждое из них.
Для любых двух натуральных чисел всегда найдется наибольший общий делитель, поскольку любые два числа всегда делятся на единицу. Если у двух натуральных чисел нет других общих делителей кроме единицы, они называются взаимно простыми. Наибольший общий делитель 12 и 18 равен 6. Для того, чтобы найти наибольший общий делитель двух чисел, нужно перемножить общие простые множители, входящие в разложение и одного, и другого числа: 1 ∙ 2 ∙ 3 = 6.
Множество Z целых чисел
Определение:
Натуральные, отрицательные натуральные числа и ноль образуют множество целых чисел (множество Z).
Сумма, произведение и разность целых чисел является целым числом, а частное — не всегда. Иногда множество отрицательных целых чисел обозначается Z_.
Множество натуральных чисел является подмножеством множества целых чисел: N ⊂ Z.
Множество Q рациональных чисел
Определение:
Рациональными числами называются числа вида 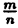
Множество целых чисел является подмножеством множества рациональных чисел, т. к. любое целое число m можно рассматривать как рациональное, представив в виде 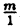
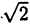
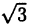
Всякое рациональное число 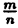
Пример:
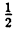
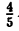
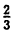
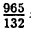
Две последние десятичные дроби бесконечные периодические. Повторяющиеся цифры называются периодом дроби и пишутся в скобках, количество этих цифр называется длиной периода. Для обратного преобразования конечной десятичной дроби ее нужно представить в виде простой и сократить: 0,8=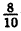
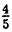
Перевод периодической десятичной дроби в простую объясним на примере.
Пример:
Записать в виде простой дроби 0,(6).
Решение:
Периодическую дробь 0,(6) обозначим за x: 0,(6)=x, тогда, т. к. 10‧х — 10-0,666… = 6,666…, легко заметить, что 10∙х = 6 х. Решая это уравнение, получаем: 9‧x=6⇔x = 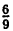
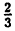
Определение:
Целой частью числа называется наибольшее целое число, не превосходящее данное. Целая часть числа х обозначается [x].
Примеры:
[3,56]=3; [0,12]=0; [-0,12]=-1; [-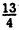
[5]=5; [0]=0.
Определение:
Дробной частью числа называется разность между самим числом и его целой частью. Дробная часть числа обозначается . Она строго меньше единицы и находится в пределах : 0 ≤ Множество J иррациональных чисел
Определение:
Иррациональным числом называется бесконечная непериодическая десятичная дробь.
Примерами иррациональных чисел являются √2, √3, ∛11, π, е, и т. д. Заметим, что J ∩Q = ⊘ Иррациональное число нельзя представить в виде простой дроби, его также невозможно ’’выписать до конца” (представить в виде конечной десятичной дроби), поэтому запись √2 = 1,41 ошибочна, следует писать √2 ≈ 1,41.
Заданное бесконечной непериодической дробью иррациональное число определяет две последовательности конечных (рациональных) десятичных дробей, называемых десятичными приближениями по недостатку и по избытку. Например, для √2 можно написать:
1 √2 Множество R действительных чисел
Определение:
Все рациональные и иррациональные числа образуют множество действительных (вещественных) чисел: R = QuJ.
В множестве действительных чисел всегда выполнимы сложение, вычитание, умножение, деление (не на ноль), возведение в любую действительную степень положительного числа, извлечение корня нечетной степени из отрицательного числа.
В множестве действительных чисел невозможно извлечение корня четной степени из отрицательного числа.
Числовая ось
Множеству действительных чисел можно дать простую геометрическую интерпретацию. Выберем на прямой положительное направление (указывается стрелкой), начало отсчета и единицу масштаба. Такая прямая называется числовой осью. Каждой ее точке можно поставить в соответствие единственное действительное число следующим образом: положительное число х изображается точкой, расположенной на оси на расстоянии х в направлении стрелки (на рис. 6 справа от О), отрицательное с другой стороны (на рис. 6 слева от О) на расстоянии х от О.
Число х называется координатой соответствующей точки на числовой оси. Из двух чисел больше будет то, которое расположено на числовой оси дальше в направлении стрелки (на рис. 6 — правее).

Числовые промежутки
Если известны два действительных числа а и b, a a>, (- ∞ ;b)= <x|x 
Числовые промежутки будем выделять штриховкой или утолщенной линией.
Примеры с решением на тему: «Множества«
При решении примеров данного практического занятия используется материал средней школы и материал лекции 1. Применение метода интервалов для решения неравенств иллюстрируется примерами 1.2-1.5
Пример:
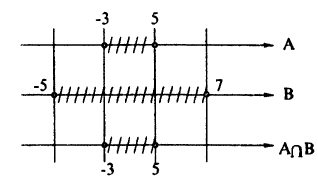
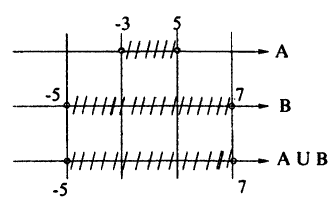
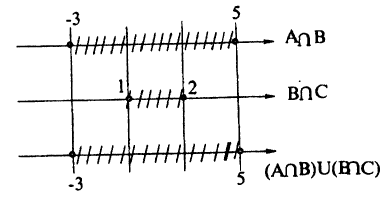
Пусть A = [-3;5],B = (-5;7),C = [1;2). Найдите множество: A₀ = (4 ∩ В) U (В ∩ С).
Решение:
Для нахождения результата операций над числовыми промежутками их удобно изображать на числовых осях, расположенных одна под другой с согласованным началом и одинаковым масштабом. Если исходные промежутки А и В заштриховать, то их пересечением будет множество точек, заштрихованных на каждой из осей (рис. 8), а их объединением — множество точек, заштрихованных хотя бы на одной из осей (рис. 9).
Пользуясь этим правилом, последовательно получим A ∩ В, В ∩C и, наконец, (Л ∩ В) ∪ (В ∩ С) (рис. 8, 10, 11).
Ответ: A₀ ≈ [-3; 5].
Пример:
Решение:
Неравенство (2 — 3x)(х + 4)(x — 2) > 0 решим методом интервалов, для чего нанесем на числовую ось значения х, при которых левая часть неравенства обращается в ноль: x₁ =
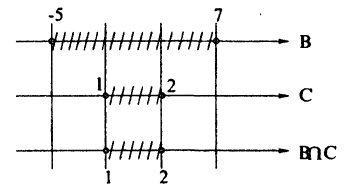
Сами эти значения не удовлетворяют неравенству, поэтому соответствующие точки “выколоты».
Знаки выражения в левой части неравенства определим, подставляя в него по одному значению из каждого интервала, на которые все множество R разбилось точками x₁,x₂,х₃. Отметим штриховкой те интервалы, на которых выражение в левой части неравенства положительно. Это множество является искомым.
Ответ: A₀=(-∞; -4) ∪ (
Пример:
Задайте характеристическим свойством множество: A₀ — множество всех натуральных чисел, меньших 5 или больших 10.
Решение:
В условии требуется,чтобы натуральные числа были меньше 5 или больше 10, т.е. искомое множество есть объединение двух подмножеств: множества натуральных чисел, меньших 5 и больших 10.
Пример:
Решите систему неравенств:
Решение:
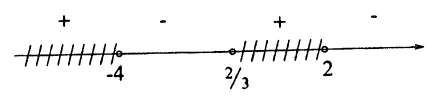
Решение системы неравенств есть пересечение множеств решений каждого из входящих в систему неравенств. Аналогично тому, как это делалось при решении примера 1.2, решим каждое из неравенств системы методом интервалов и найдем их пересечение (рис 13).
Пример:
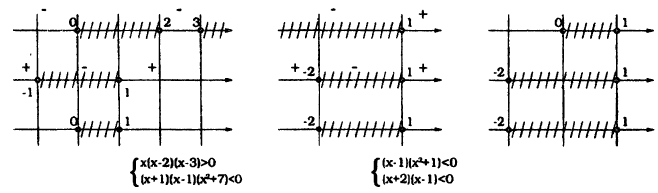
Решите совокупность систем неравенств:
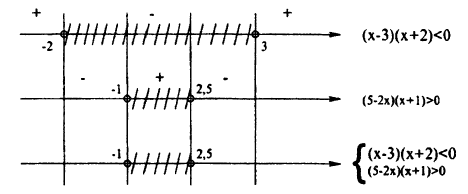
Решение:
Решение совокупности систем неравенств есть объединение решений каждой системы, входящей в совокупность. Для решения разложим каждый многочлен в произведение с помощью корней:
Решение совокупности систем методом интервалов представлено на рис. 14
Видео:Универсальное множество и абсолютное дополнение (видео 4)| Множества | АлгебраСкачать

Множества
Понятие множества является одним из основных понятий математики. Оно не сводится к другим понятиям и не определяется. Вместо определения приводят лишь примеры, поясняющие его смысл. Так, можно говорить о множестве всех учеников данной школы, о множестве всех собак на земном шаре, о множестве всех клеток данного человеческого тела, о множестве всех картофелин в данном мешке, о множестве всех натуральных чисел, о множестве всех треугольников на данной плоскости, о множестве всех точек данного круга и т. д.
Когда в математике говорят о множестве, то объединяют некоторые предметы в одно целое — множество, состоящее из этих предметов. Основатель теории множеств Георг Кантор (1845—1918) выразил это следующими словами: «Множество есть многое, мыслимое как единое».
Предметы (объекты), составляющие некоторое множество, называются его элементами. То обстоятельство, что объект а является элементом множества А, записывается так: 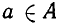
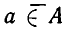
Например, если А есть множество всех четных натуральных чисел, то
Множество иногда можно задать перечислением всех его элементов. В этом случае употребляют фигурные скобки, в которые помещают названия всех элементов множества, разделенные запятыми. Так, <1, 2, 3) обозначает множество, состоящее из чисел «один», «два», «три» и только из них.
Вообще некоторое множество считается заданным, если указано некоторое свойство, которым обладают все его элементы и не обладают никакие другие объекты. Такое свойство называется характеристическим свойством множества.
Числовые множества
Множества могут состоять из объектов самой различной природы. Их элементами могут быть буквы, атомы, числа, уравнения, точки, углы и т. д. Именно этим объясняется чрезвычайная широта теории множеств и ее приложимость к самым разным областям знания (математике, механике, физике, лингвистике, экономике и т. д.). Для математики особо важную роль играют множества, составленные из «математических» объектов— корней уравнений, геометрических фигур и т. д. Чаще всего нам будут встречаться числовые множества, то есть множества, элементами которых являются числа. Примерами числовых множеств являются: а) множество всех действительных чисел; б) множество всех рациональных чисел; в) множество всех положительных чисел; г) множество всех чисел, удовлетворяющих неравенству 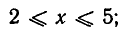
Некоторые числовые множества имеют особые названия. Если даны два числа а и b, а
если это не вызывает недоразумений, просто отрезком и обозначают [а, b]. На числовой оси ему соответствует отрезок с концами а и b (рис. 1).
Множество чисел, удовлетворяющих неравенству а а (или х
(или (—
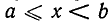
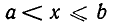
конец включается в множество, а круглая — что он исключается.
Пустое множество
Введение понятия множества в математику оказалось очень полезным. Из-за того что элементами множеств могут быть вещи самой различной природы, одни и те же утверждения, касающиеся множеств, можно истолковать и как утверждения о натуральных числах, и как утверждения о точках геометрических фигур, и как утверждения о множестве слов и т. д. Таким образом, понятия и теоремы теории множеств обладают большой общностью. Этим и объясняется то, что язык теории множеств применяется в самых различных областях математики.
В математике приходится иногда рассматривать множества, содержащие только один элемент, и даже множества, не имеющие ни одного элемента. Множество, не содержащее ни одного элемента, называют пустым. Его обозначают знаком 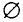
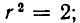
О некотором множестве может быть неизвестно, является ли оно пустым множеством или нет. Так, до сих пор неизвестно, пусто ли множество натуральных чисел n таких, что n > 2, а уравнение
имеет положительные целочисленные решения (в этом состоит известная проблема Ферма).
Пустое множество единственно: нет двух разных пустых множеств.
Подмножество
Пусть даны два множества A и B, причем каждый элемент первого множества является элементом второго множества. Тогда множество А называют подмножеством (или частью) множества В. В этом случае пишут:
Примеры подмножеств: а) числовой отрезок [1,3] есть подмножество числового отрезка [0, 4];
б) множество всех квадратов есть подмножество множества всех прямоугольников; в) множество всех целых чисел есть подмножество множества всех рациональных чисел.
Отметим, что пустое множество 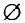
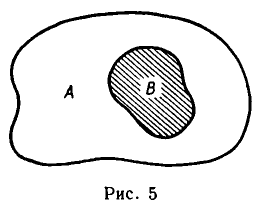
Множества часто изображают наглядно как множество точек геометрической фигуры. Тогда подмножество — это множество то чек части фигуры (рис. 5).
Пересечение множеств
Пусть даны множества А, В, С, … . Их пересечением называют множество X, содержащее те и только те элементы, которые входят в каждое из заданных множеств. Пере сечение двух множеств А и В обозначают АВ или
Если множества А и В состоят из точек некоторых геометрических фигур, то 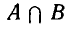
Пересечение множеств называют также их произведением, а операцию пересечения — умножением множеств. Можно показать,
что многие свойства пересечения множеств напоминают свойства умножения чисел.
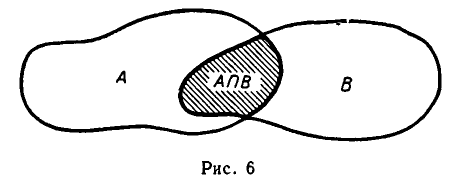
Примеры пересечения множеств: а) пересечением числового отрезка [0, 4 ] с числовым отрезком [2, 5] является числовой отрезок [2, 4] (рис. 7);
б) пересечение числового отрезка [0, 2] с числовым отрезком [3, 5] пусто; в) пересечение множества всех ромбов с множеством всех прямоугольников есть множество всех квадратов; г) пересечением множества четных натуральных чисел с множеством натуральных чисел, делящихся на 3, является множество натуральных чисел, делящихся на 6.
Сложение множеств
Суммой (или объединением) множеств А, В, С, . . . называют множество X, состоящее из тех и только тех элементов, которые входят хотя бы в одно из этих («слагаемых») множеств. Сумму двух множеств А и В обозначают А + В или 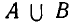
Если какой-нибудь элемент входит в несколько слагаемых множеств, то в сумме он берется лишь один раз. Например, суммой числового отрезка [0, 4] и числового отрезка [2, 5] является числовой отрезок [0, 5]. При этом точки отрезка [2, 4] входят в оба слагаемые, но в сумме они берутся лишь один раз. Впрочем, выражения «некоторый элемент берется в данном множестве пять раз» и т. п., как это следует из принятого нами понимания терминов «множество» и «элемент», просто не имеют смысла.
Примеры а) Обозначим через А множество точек некоторой плоской области и через В — множество точек другой области (рис. 8). Тогда их суммой будет множество точек заштрихованной фигуры, ограниченной на рис. 8 жирной линией. б) Обозначим через А множество успевающих учеников в классе, через В — множество девочек в этом классе и через С — множество неуспевающих мальчиков. Тогда 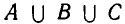
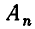
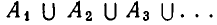
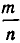
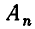
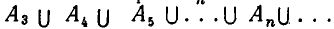
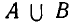
Разбиение множеств
Пусть множество X является суммой множеств A, В, С. . . , причем никакие два из них не имеют общих элементов. Тогда говорят, что множество X разбито на (непересекающиеся) подмножества А, В, С, . . . .
Примеры разбиения множеств: а) Множество натуральных чисел разбивается на подмножества четных чисел и нечетных чисел. б) Множество всех учеников в классе разбивается на множества учеников, фамилия которых начинается на букву «А», учеников, фамилия которых начинается на букву «Б», и т. д. вплоть до буквы «Я». Какое из этих множеств пусто, если взять ваш класс? Какие из этих множеств пусты для любого класса? в) Множество всех векторов на плоскости можно разбить на непересекающиеся подмножества, относя к одному подмножеству все векторы, равные друг другу по длине, параллельные и одинаково направленные. г) Это же множество можно разбить иначе, относя к одному под множеству векторы, выходящие из одной точки плоскости.
Вычитание множеств
Если даны два множества A и В, то их разностью называют такое множество X = A В или (А — В), в которое входят все элементы из Л, не принадлежащие множеству В. При этом не предполагается, что множество В является частью множества A. Таким образом, при вычитании множества В из множества A из A удаляют общую часть (пересечение) A и В:
Например, если A — множество всех учащихся IX класса данной школы, а В — множество всех девочек, которые учатся в этой школе, то A В — множество всех мальчиков, обучающихся в IX классе этой школы.
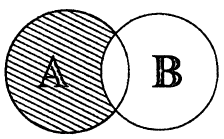
В случае, когда В — часть множества А, А В называют дополнением к В в множестве А и обозначают 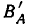
Отображение множеств
Пусть даны два множества X и У и пусть имеется правило 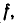
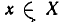
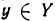
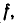
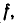
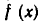
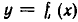
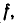
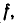

Если всякий 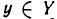
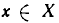



Приведем примеры отображений множеств: а) Пусть X — множество всех действительных чисел, У — множество всех неотрицательных чисел. Равенство 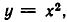
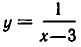
Пусть 
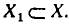
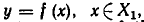
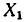

Рассмотрим некоторый элемент у из множества У и возьмем все элементы х из X, отображающиеся в у при отображении 

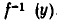
Если полный прообраз каждого элемента у из У при отображении 

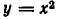
Если 

Краткие исторические сведения
Теоретико-множественные представления в неявной форме давно использовались математиками. Геометры древней Греции в III веке до н. э. рассматривали «геометрические места точек», то есть множества точек, обладающих тем или иным свойством. Однако трудности, связанные с понятием бесконечности, привели к тому, что в течение длительного времени математики избегали рассматривать геометрические фигуры как множества точек.
Исследования по бесконечным множествам начали чешский ученый Б. Больцано (1781— 1841) и немецкий математик Г. Кантор (родился в 1845 г. в Петербурге, умер в 1918 г. в Галле). Труд Больцано был опубликован лишь через много лет после его смерти. Основные заслуги в развитии теории множеств принадлежат Кантору. Он пришел к проблемам этой теории, исходя из сравнительно узкой математической задачи (вопроса о сходимости и расходимости тригонометрических рядов). Однако вскоре ему и его последователям стало ясно, что теория множеств имеет важнейшее значение для различных областей математики. Сейчас теория множеств дает общепринятый язык для многих разделов математики. В целом ряде случаев применение теоретико-множественных понятий позволило привести в систему многие ветви математики. Большой вклад в теорию множеств сделан трудами советских математиков П. С. Александрова, А. Н. Колмогорова, Н. Н. Лузина, П. С. Новикова, М. Я. Суслина и других. Советская школа теории множеств оказала сильное влияние на развитие этой части математики во всем мире.
Вскоре после создания теории множеств выяснилось, что «наивная» трактовка понятия бесконечного множества может привести к противоречиям. Исследования в этом направлении потребовали развития математической логики. Первоначально эта область математики была очень далека от практических приложений, но впоследствии ее принципы составили идейную основу конструирования электронных вычислительных машин и программирования вычислений на этих машинах.
Правила действий над высказываниями, во многом известные еще Аристотелю (создателю формальной логики), были более подробно сформулированы Г. В. Лейбницем, которого часто считают создателем математической логики. Алгебраическую форму этим правилам придали английские математика Дж. Буль (1815— 1864) и А. де Морган (1806—1871). По сути дела, эти правила совпадают с указанными выше правилами действий над множествами. Большой вклад в развитие математической логики внесли Г. Фреге, Б. Рассел, Д. Гильберт, К. Гёдель, А. Тарский, советские математики П. С. Новиков, А. Н. Колмогоров, А. А. Марков и другие.
Видео:ПОДМНОЖЕСТВА. Операции над множества. §14 алгебра 8 классСкачать

Дополнение к различным типам множеств










Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Видео:Операции над множествамиСкачать

Дополнение к множеству треугольников
Введение в теорию множеств и комбинаторику
Практическая работа №3. Действия над множествами
Вопросы к работе
1. Что такое “объединение двух множеств”?
2. Сформулируйте и запишите необходимое и достаточное условие попадания элемента х в объединение множеств А и В .
3. Сформулируйте и запишите необходимое условие нахождения элемента х в объединении множеств А и В .
4. Что такое “пересечение двух множеств”?
5.Сформулируйте и запишите необходимое и достаточное условие попадания элемента х в пересечение множеств А и В .
6.Сформулируйте и запишите необходимое и достаточное условие нахождения элемента х в пересечении множеств А и В .
7. Что такое “разность множеств А и В ”?
8. Сформулируйте и запишите необходимое и достаточное условие попадания элемента х в разность множеств А и В .
9. Сформулируйте и запишите необходимое и достаточное условие невхождения элемента х в разность множеств А и В .
10. Что такое “дополнение множества А до множества В ”? Какое его обозначение?
11. Сформулируйте и запишите необходимое и достаточное условие попадания элемента х в дополнение множества А до множества В .
12. Сформулируйте и запишите необходимое и достаточное условие невхождения элемента х в дополнение множества А до множества В .
13. Что такое “универсальное множество для данной системы множеств”? Приведите примеры.
14. Что такое “дополнение данного множества”? Как оно обозначается?
15. Сформулируйте и запишите необходимое и достаточное условие попадания элемента х в дополнение множества А .
16. Сформулируйте и запишите необходимое и достаточное условие невхождения элемента х в дополнение множества А .
17. Укажите диаграммы Эйлера-Венна для объединения множеств А и В , пересечения множеств А и В , разности множеств В и А , разности множеств А и В , дополнения множества А до множества В , дополнения множества А.
Образцы решения заданий
Пример 1. Найдите объединение, разность и пересечение множеств А и В , если
А = < x 







Решение. Если изобразить данные множества на числовой прямой, то объединение А 

А 



Пример 2. Доказать, что для любых множеств А , В , С верно:
А 




Решение. 1) Пусть А ≠ Ø, В ≠ Ø, С ≠ Ø. Обозначим А 




а) если x 

б) если x 

Рассмотрим случай (а):
Итак, если x 

Значит, 
2) Если А = Ø, то М 1 = В 

Если В = Ø, то М 1 = А 


М 1 = М 2.
Аналогично, если C = Ø. Если А = В = С = Ø , то М 1 = Ø, М 2. = Ø,
т. е. М 1 = М 2.
В итоге мы можем сказать: для любых множеств А , В и С верно:
А 


Пример 3. Доказать, что для любых множеств А и В верно:



Решение. 1) Пусть А 




Значит, М 1 

2) Если А= Ø , то М 1 = 


Аналогично, если В = Ø.
3) Если А = В = Ø , то М 1 =J, М 2. = J 
1. Найдите объединение, пересечение, разность множеств А и В , если
а) А = 
б) А = 

в) А = 

2. Даны множества: А – тупоугольных треугольников, В – прямоугольных треугольников, С – треугольников с углом в 50 0 . Постройте для данных множеств диаграмму Эйлера-Венна, выделив штриховкой область, изображающую множество ( А 

3. S – множество правильных многоугольников, Т – множество прямоугольников. Из каких фигур состоит пересечение и объединение множеств S и Т . Какие из фигур, изображенных на рис 9, принадлежат пересечению множеств S и Т , а какие – их объединению?
4. А – множество натуральных чисел, кратных 3, В – множество натуральных чисел, кратных 7. Задайте характеристическим свойством элементов множество А В и назовите три числа, принадлежащих этому множеству.
5. Пусть А = , В = , С =. Найти длину множества:
а) А 

б) ( С 

в) А 

г) А 

д) А 

а) – 4 

б) 0 

в) 13 

7. Найдите дополнение к множеству А до множества Z , если
8. Найдите дополнение в множестве всех треугольников к множеству:
а) всех равносторонних треугольников;
б) всех равнобедренных треугольников;
в) всех прямоугольных треугольников.
9. Для любых множеств А , В, С доказать, что:
а) А 




б) А 

в) А 

г) А 
д) А 
е) В 
ж) ( А В ) С = ( А С ) ( В С );
з) А ( А В ) = А 
и) В 

Результат проиллюстрировать на кругах Эйлера – Венна.
10. Докажите, что для любых подмножеств А и В универсального множества J справедливы следующие равенства:
1. Даны следующие пары множеств:
8) А = < х|х = 2 n, n 

9) А – множество нечетных натуральных чисел,
В – множество простых чисел, больших чем 2;
10) А – множество четных натуральных чисел,
В – множество простых чисел, больших чем 2.
Задание: а) найдите для каждой пары подходящее универсальное множество;
б) связаны ли пары одним из соотношений: =, 

в) найдите пересечение А 
г) найдите разность А В ;
д) найдите А 
е) изобразите каждую пару множеств при помощи диаграмм Эйлера-Венна.
2. Проверьте равенство множеств
1) а) А 




б) 


в) ( А В ) С = ( А В ) ( С В ).
2) а) А 




б) В А = ( А 


в) А ( В С ) = ( А С ) ( В С ).
3) а) 




б) В А = ( А 


в) ( А В ) С = ( А С ) ( В С ).
4) а) А 





б) В А = ( А 



в) ( А В ) С = ( А В ) 
5) а) А 


б) А 

в) А ( В 
6) а) А 


б) А 



в) А 

7) а) 




б) А 




в) ( А С ) С = ( А В ) 
8) а) А 



б) А 



в) А ( В С ) = ( А В ) 
9) а) А 
б) 




в) А 

10) а) А 


б) В А = ( 



в) ( А В ) С = А ( В 
Вопросы для самопроверки.
- Множества А , В, С изображены с помощью кругов Эйлера-Венна. Множество М – результат некоторого действия с множествами А , В, С – отмечено в диаграмме Эйлера-Венна штриховкой. Записать два варианта формул получения множества М через множества А, В, С.
📺 Видео
Подмножество. 5 класс.Скачать

Мир чисел | дополнение множестваСкачать

Самый короткий тест на интеллект Задача Массачусетского профессораСкачать

Множества. Операции над множествами. 10 класс алгебраСкачать

Пересечение множеств. Объединение множеств. 5 класс.Скачать

Альтернативные операции дополнения нечёткого множестваСкачать

Урок 50. Операции над множествами. Пересечение, объединение. (6 класс)Скачать

5 класс Математика. 2.2. Подмножества. Дополнение множествСкачать

Простейшие операции над множествамиСкачать

A.2.9 Пересечение, объединение и симметрическая разность множествСкачать