Доклад на тему параллельные прямые 6 класс (2 видео)

Доклад на тему параллельные прямые 6 класс

Параллельные прямые — две прямые, которые лежат в одной плоскости и не пересекаются, а || b.

Слово «параллельный» от греческого «parallelos» — идущий рядом. Знак параллельности || впервые встречается в трудах У. Оутреда (1677 г).

Аксиома параллельности:
Через точку, не лежащую на данной прямой, на плоскости можно провести только одну прямую , параллельную данной прямой.

Выделенная синим цветом часть этого утверждения — знаменитый пятый постулат Евклида. Отказ от пятого постулата ведёт к геометрии Лобачевского. В геометрии Лобачевского через точку, лежащую за прямой, проходит множество прямых, которые не пересекают данную прямую.

Иногда Аксиому параллельных прямых принимают в качестве одного из свойств параллельных прямых, но вместе с тем на ее справедливости строят другие геометрические доказательства.

Примечание. В планиметрии две различные прямые либо пересекаются, либо параллельны. В стереометрии возможен третий вариант — прямые могут не пересекаться, так как не лежат в одной плоскости. Такие прямые называются скрещивающимися.

Содержание

Свойства и признаки параллельных прямых
Параллельные прямые
Понятие параллельных прямых
Готовые работы на аналогичную тему
Историческая справка
Параллельные прямые в жизни
Параллельные прямые в архитектуре
Параллельные прямые
Что такое параллельные прямые
Аксиома параллельных прямых
Фигуры с параллельными прямыми
Что мы узнали?
🔍 Видео

Свойства и признаки параллельных прямых

Свойства и признаки параллельных прямых:

Две прямые, параллельные третьей, параллельны.
Через точку, не лежащую на данной прямой, можно провести одну и только одну прямую, параллельную данной.
Если прямая пересекает одну из параллельных прямых, то она пересекает и другую.
Если прямая перпендикулярна одной из параллельных прямых, то она перпендикулярна и другой.
Если две параллельные прямые пересечены секущей, то:
– сумма внутренних односторонних углов равна 180°,
– накрест лежащие углы равны,
– соответственные углы равны,

Теорема Фалеса:
Если на одной из двух прямых отложено несколько равных отрезков и через их концы проведены параллельные прямые, не пересекающие другую прямую, то и на ней отложатся равные отрезки.

Это конспект по теме «Параллельные прямые». Выберите дальнейшие действия:

Видео:Параллельные прямые. 6 класс.Скачать

Параллельные прямые

Вы будете перенаправлены на Автор24

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Понятие параллельных прямых

Параллельные прямые – прямые, которые лежат в одной плоскости, не совпадают и не имеют общих точек.

Если у прямых есть общая точка, тогда они пересекаются.

Если все точки прямых совпадают, то имеем по сути одну прямую.

Если прямые лежат в разных плоскостях, то условий их параллельности несколько больше.

При рассмотрении прямых на одной плоскости можно дать следующее определение:

Две прямые на плоскости называют параллельными, если они не пересекаются.

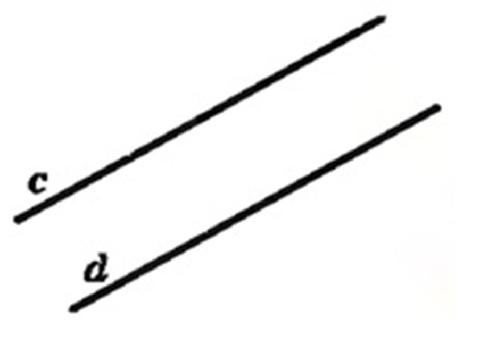
В математике параллельные прямые принято обозначать с помощью знака параллельности « $parallel$ ». Например, тот факт, что прямая $c$ параллельна прямой $d$ обозначается следующим образом:

Зачастую рассматривается понятие параллельных отрезков.

Два отрезка называют параллельными, если они лежат на параллельных прямых.

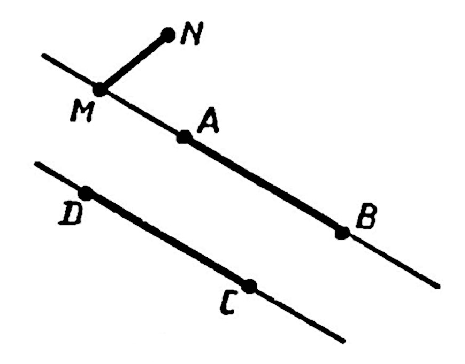
Например, на рисунке параллельными являются отрезки $AB$ и $CD$, т.к. они принадлежат параллельным прямым:

Вместе с тем, отрезки $MN$ и $AB$ или $МN$ и $CD$ параллельными не являются. Этот факт можно записать с помощью символов следующим образом:

Готовые работы на аналогичную тему

$MN ∦ AB$ и $MN ∦ CD$.

Аналогичным образом определяется параллельность прямой и отрезка, прямой и луча, отрезка и луча или двух лучей.

Видео:6 класс, 44 урок, Параллельные прямыеСкачать

Историческая справка

С греческого языка понятие «параллелос» переводится «рядом идущий» или «проведенный друг возле друга». Этот термин использовался в древней школе Пифагора еще до того, как параллельные прямые получили свое определение. Согласно историческим фактам Евклидом в $III$ в. до н.э. в его трудах все же был раскрыт смысл понятия параллельных прямых.

В древности знак для обозначения параллельных прямых имел отличный вид того, что мы используем в современной математике. Например, древнегреческим математиком Паппом в $III$ в. н.э. параллельность обозначалась с помощью знака равенства. Т.е. тот факт, что прямая $l$ параллельна прямой $m$ ранее обозначался «$l=m$». Позднее для обозначения параллельности прямых стали использовать привычный нам знак «$parallel$, а знак равенства стали использовать для обозначения равенства чисел и выражений.

Видео:Параллельные прямые, 6 классСкачать

Параллельные прямые в жизни

Зачастую мы не замечаем, что в обычной жизни нас окружает огромное число параллельных прямых. Например, в нотной тетради и сборнике песен с нотами нотный стан выполнен с помощью параллельных линий. Также параллельные линии встречаются и в музыкальных инструментах (например, струны арфы, гитары, клавиши фортепиано и т.п.).

Электрические провода, которые расположены вдоль улиц и дорог, также проходят параллельно. Рельсы линий метро и железных дорог располагаются параллельно.

Кроме быта параллельные линии можно встретить в живописи, в архитектуре, при строительстве зданий.

Видео:Перпендикулярные и параллельные прямые. Математика 6 классСкачать

Параллельные прямые в архитектуре

На представленных изображениях архитектурные сооружения содержат параллельные прямые. Использование параллельности прямых в строительстве помогает увеличить срок службы таких сооружений и придает им необычайную красоту, привлекательность и величие. Линии электропередач также умышленно проводятся параллельно, чтобы избежать их пересечения или соприкосновения, что привело бы к замыканию, перебоям и отсутствию электричества. Чтобы поезд мог беспрепятственно перемещаться рельсы также выполнены параллельными линиями.

В живописи параллельные линии изображают сводящимися в одну линию или близкими к тому. Такой прием называется перспективой, которая следует из иллюзии зрения. Если долго смотреть вдаль, то параллельные прямые будут похожи на две сходящиеся линии.

Видео:Перпендикулярные прямые. 6 класс.Скачать

Параллельные прямые

Средняя оценка: 4.7

Всего получено оценок: 98.

Средняя оценка: 4.7

Всего получено оценок: 98.

Параллельные прямые находятся повсюду в нашей жизни. Они – основа симметрии, которая, так или иначе, присутствует в каждом элементе мебели, архитектуре и орудиях труда. Знание определения и свойств параллельных прямых помогают не только при решении задач по математике 6 класса, но и при расчетах реальных предметов быта.

Видео:Урок ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕСкачать

Что такое параллельные прямые

Параллельными прямыми называют прямые, которые не пересекаются.

В этом определении параллельных прямых есть небольшая неточность: прямые, которые имеют больше одной общей точки, совпадают. Иногда о них также говорят, как о параллельных.

Прямая, пересекающая параллельные прямые, называется секущей. При пересечений образуется 8 углов. Друг относительно друга они могут быть соответственными, односторонними и накрест лежащими. Рассмотрим их на примере.

Рис. 1. Виды углов.

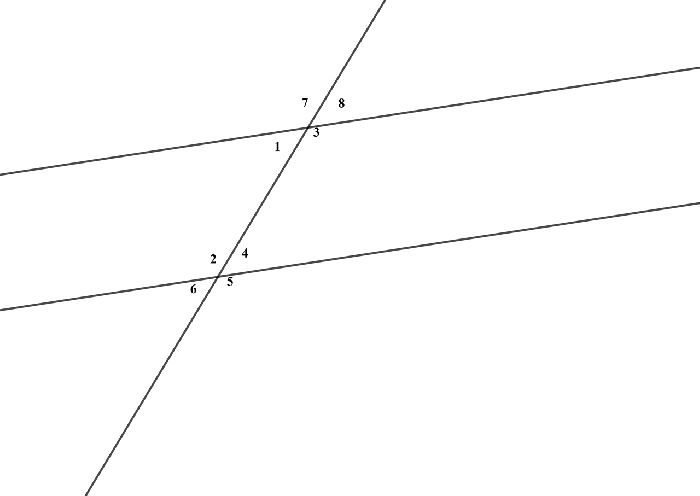
Соответственные углы: 7 и 2, 1 и 6, 8 и 4, 3 и 5
Накрест лежащие: 7 и 5, 8 и 6, 1и 4, 3 и 2
Односторонние: 1и 2, 3 и 4, 7 и 6, 8 и 5

Видео:Параллельные прямые | Математика 6 класс #44 | ИнфоурокСкачать

Аксиома параллельных прямых

Аксиома параллельных прямых – это одно из основных утверждений геометрии. Через точку можно провести прямую, параллельную данной, и при том только одну – это наиболее распространенная формулировка аксиому.

Из аксиомы есть два следствия:

Если прямая параллельна одной из двух параллельных прямых, то она параллельна и второй.
Если прямая пересекает одну из параллельных прямых, то она пересечет и вторую.

Обратите внимание, что аксиома справедлива только для плоскости. В пространстве может быть вариант, когда прямая параллельна плоскости, в которой будет бесконечное множество параллельных ей прямых, проходящих через одну точку. Значит в пространстве это условие не обязательно выполняется.

Расстояние между параллельными прямыми в любой точке будет одинаковым и равным величине отрезка, перпендикулярного каждой из прямых.

Видео:Математика 6 класс: Параллельные и перпендикулярные прямыеСкачать

Фигуры с параллельными прямыми

Существует множество фигур, при построении которых используются параллельные прямые. Например, параллелограмм состоит из двух попарно параллельных отрезков.

Квадрат и прямоугольник также состоят из попарно параллельных прямых, но при этом они являются частным случаем параллелограмма.

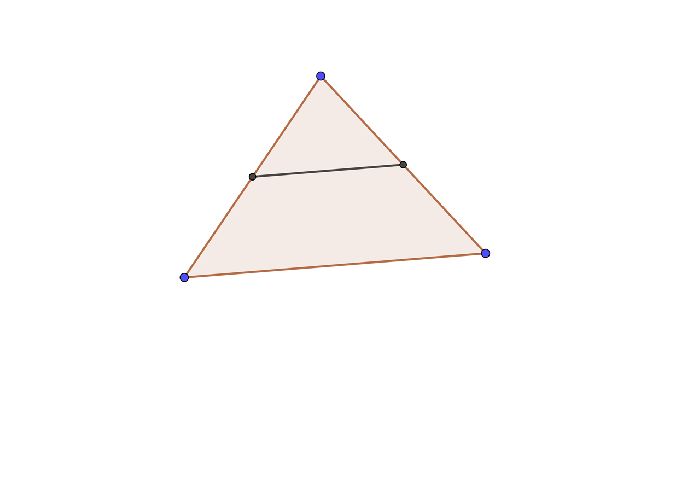
В треугольнике средняя линия всегда параллельна основанию.

Рис. 2. Средняя линия треугольника.

Также есть еще одна интересная фигура: трапеция. В трапеции большое и малое основание параллельны друг другу, а боковые стороны не параллельны.

Рис. 3. Трапеция.

Если прямые непараллельны, то они пересекаются, но если не параллельны отрезки, это вовсе не значит, что они пересекутся. Отрезки имеют конечное значение длинны, а поэтому могут просто стоять отдельно друг от друга. При этом, отдельных видов или каких-либо таблиц параллельных прямых нет, и вряд ли они когда-нибудь появятся.

Видео:Геометрия 7 класс (Урок№18 - Параллельные прямые.)Скачать

Что мы узнали?

Мы узнали все о параллельных прямых, привели аксиому параллельных прямых и следствия из нее. Поговорили о различии понятий параллельных прямых и параллельных отрезков, а также выяснили, почему аксиома для параллельных прямых работает только на плоскости. Привели примеры фигур, для построения которых требуются параллельные прямые.