- Главная
- Список секций
- Математика
- КРУГИ ЭЙЛЕРА
- КРУГИ ЭЙЛЕРА
- Менее 30 дней
- осталось до конца вашей подписки
- Получить в подарок обзор книги «Законы влияния» Сьюзан Вайншенк.
- Получите бесплатно обзор этой книги на свой email прямо сейчас.
- Оставьте свой email и вы сможете скачать «Алгоритм написания текстов»
- Спасибо!
- Спасибо!
- Спасибо!
- Спасибо!
- Спасибо!
- Спасибо!
- Спасибо!
- Заказ подписки
- Заказ подписки
- Круги Эйлера
- Для чего нужны круги Эйлера
- Типичный пример кругов Эйлера
- Пример решения задачи с помощью кругов Эйлера
- Резюме
- Исследовательская работа «Круги Эйлера»
- «Управление общеобразовательной организацией: новые тенденции и современные технологии»
- 🎦 Видео
Видео:Окружность девяти точек, Эйлера, Фейербаха, Теркема...Скачать

КРУГИ ЭЙЛЕРА
Автор работы награжден дипломом победителя III степени
Круги Эйлера — это геометрическая схема, с помощью которой можно наглядно изобразить отношения между различными множествами и подмножествами. Такая схема помогает находить логические связи между явлениями и понятиями, она изобретена Леонардом Эйлером, используется в математике и других научных дисциплинах. Использование Кругов Эйлера упрощает рассуждения и помогает быстрее и проще получить ответ. (1),(2)
Круги Эйлера неотрывно связаны с понятием множества. Поэтому, чтобы лучше понимать, что изображено на кругах Эйлера, нужно знать, что такое множество и какие множества бывают.
Под множеством можно понимать совокупность каких-либо объектов, называемых элементами множества. Во множества можно объединять любые объекты с общим признаком. Например, множество учеников гимназии 11, учащихся в 7 «Б» классе составляют отдельное множество. Множества могут быть и неодушевленных предметов. Например, множество книг, написанных каким-либо автором. С помощью кругов Эйлера множество обозначается, как пустой круг, а входящие в него элементы – точками. (5)
Давайте изобразим множество цифр. На рисунке контуром обозначено множество, а точками элементы этого множества.
Множества бывают трех видов:
· Конечное (например — множество цифр)
· Бесконечное (например — множество чисел)
· Пустое (множество натуральных чисел
Группа предметов, образующая множество, входящее в состав более обширного множества, изображается в виде меньшего круга, нарисованного внутри большего круга, и называется подмножеством. Такое отношение образуется между большим множеством животных и входящим в его состав подмножеством плоских червей. (5)
В тех случаях, когда два понятия совпадают только частично, отношение между такими множествами изображается с помощью двух перекрещивающихся кругов. Такое отношение образуется между множеством учащихся 7 «Б» класса и множество троечников. Некоторые элементы множества учеников 7 «Б» класса принадлежат и к множеству троечников. (5)
Когда ни один предмет, из одного множества, не может одновременно принадлежать второму множеству, то отношение между ними изображается посредством двух кругов, нарисованных один вне другого. Такими множествами являются множество отрицательных и множество положительных чисел. (5)
Круги Эйлера были изобретены и названы в честь Леона́рда Э́йлера (портрет слева). Это был швейцарский математик, внёсший значительный вклад в развитие математики, а также механики, физики, астрономии и ряда прикладных наук. Эйлер родился в Швейцарии, учился в Германии, но работал и умер в России. Этот ученый – автор 800 работ. Леонард Эйлер родился в 1707 году в семье пастора. Его отец был другом семьи Бернулли. У Эйлера рано проявились математические способности. Обучаясь в гимназии, мальчик увлечённо занимался математикой, а позже стал посещать университетские лекции Иоганна Бернулли. 20 октября 1720 года Леонард Эйлер стал студентом факультета искусств Базельского университета. Одаренный молодой человек обратил на себя внимание профессора Иоганна Бернулли. Он передал студенту математические статьи для изучения, а также пригласил приходить к нему домой, чтобы совместно разбирать непонятное. В доме своего учителя Эйлер встретился и начал общаться с сыновьями Бернулли — Даниилом (портрет слева) и Николаем (потрет справа), которые тоже занимались математикой. (6)
Юный Эйлер написал несколько научных работ. «Диссертация по физике о звуке» получила благоприятный отзыв. В то время число научных вакансий в Швейцарии было невелико. Поэтому братья Даниил и Николай Бернулли уехали в Россию, где начинала создаваться Российская Академия наук; они обещали похлопотать там и о должности для Эйлера. В начале зимы 1726 года Эйлеру пришло письмо из Санкт — Петербурга: по рекомендации братьев Бернулли он приглашён на должность адъюнкта по физиологии с окладом 200 рублей. Эйлер провёл много времени в России, где внёс существенный вклад в российскую науку. С 1731 был избран академиком Петербургской Академии. Хорошо знал русский язык, а сочинения и учебники публиковал на русском. (6)
Тогда Эйлер подробно описывает свой метод решения некоторых задач при помощи кругов Эйлера. В 1741 году Эйлер пишет «Письма о разных физических и философических материях, к некоторой немецкой принцессе..», где упоминаются «круги Эйлера». Эйлер писал, что «круги очень подходят для того, чтобы облегчить наши размышления». (3)
Метод Эйлера получил заслуженное признание и популярность. И после него немало ученых использовали его в своей работе, а также видоизменяли по-своему. Бернард Больцано использовал тот же метод, но с прямоугольными схемами. Благодаря вкладу Венна метод даже называют диаграммами Венна или еще Эйлера-Венна. Круги Эйлера имеют прикладное назначение, то есть с их помощью на практике решаются задачи на объединение или пересечение множеств в математике, логике, менеджменте и не только. (1)
Вот несколько задач для решения, которых, удобно использовать круги Эйлера:
Задача 1.
У ребят из одной школы спрашивали об их домашних животных. 100 из них ответили, что у них дома есть собака и/или кошка. У 87 ребят была одна собака, а у 63 ребят – одна кошка. У скольких ребят есть и собака и кошка?
Решение:
Чтобы решить эту задачу, не используя круги Эйлера нужно подсчитать, сколько собак и кошек было у учеников. Для этого нужно сложить 87 и 63. 87+63=150 домашних животных. Учеников было всего лишь 100, а дробного числа домашних животных получиться не может. Значит если у каждого ученика 1 домашнее животное, остается еще 50 лишних. Следовательно, у 50 учеников 2 домашних животных. И так как в задаче указано, что ни у одного из учеников нет 2 кошек или 2 собак, то это значит, что у 50 учеников есть и кошка и собака.
Но этот способ долгий и подходит только для простых задач. Такую задачу намного удобнее решить через круги Эйлера.
Красным кругом изобразим множество обладателей собак, а синим множество обладателей кошек. Всего учеников было 100. Тех, у кого есть и кошка, и собака Х. Чтобы найти количество учеников, у которых только собака нужно из 87 вычесть Х. Так как всего учеников 100, мы получаем:
Ответ: у 50 учеников есть и кошка и собака
Задача 2.
Однажды учеников спросили, кто из них любит математику, кому нравится русский язык, а кому физика. Оказалось, что из 36 учеников 2 не любят ни математику, ни русский, ни физику. Математика нравится 25 ученикам, русский язык- 11, физика – 17 ученикам; и математика, и русский- 6; и математика, и физика- 10; русский язык и физика — 4.
Сколько человек любят все три предмета?
Решение:
Изобразим 3 множества. Красное множество тех, кто любит математику, синие тех, кто любит русский язык, зеленое – физику.
Теперь впишем в множества количество элементов. 6 человек любят и русский и математику. Из них X человек любят еще и физику. Значит, только математику и русский любят 6-Х человек. Только математику и физику 10-Х, только русский и физику 4-Х человек. 25 человек любят математику. Но Х, 6-Х, 10-Х человек любят и другие предметы. Значит, только математику любят 25-(6-Х)-(10-Х)-Х= 25-6+Х-10+Х -Х=5+Х человек. Только русский любят 11-(6-Х)-(4-Х)-Х= 11-10+2Х-Х=1+Х учеников, только физику 17-(10-Х) –(4-Х)-Х= 17-14+2Х-Х= 3+Х.
Так как 2 человека не любят ни один из этих предметов, то:
Ответ: 1 человек любит все три предмета
Задача 3.
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
Видео:#207. Окружность девяти точек | лемма о трезубце | ортотреугольник | прямая ЭйлераСкачать

Менее 30 дней
Видео:Прямая ЭйлераСкачать

осталось до конца вашей подписки
Продлите подписку сейчас и не пропустите ни одной самой важной книги, способной изменить вас и ваш бизнес!
Получить в подарок обзор книги «Законы влияния» Сьюзан Вайншенк.
Получите бесплатно обзор этой книги на свой email прямо сейчас.
Оставьте свой email и вы сможете скачать «Алгоритм написания текстов»
Видео:Круги Эйлера. Логическая задача на множества. Иностранные языкиСкачать

Спасибо!
Мы будем отправлять вам только интересные и полезные новости!
Видео:16 задание. Профильный ЕГЭ 2023. 9 точек окружности, окружность Эйлера. Что это?Скачать

Спасибо!
Обновите страницу, чтобы статья открылась для чтения.
Видео:11 класс, 49 урок, Задача ЭйлераСкачать

Спасибо!
Файл доступен вам по ссылке.
Apple
для вас идеален формат epub. Абсолютно все устройства Apple автоматически его распознают и открывают через стандартное приложение iBooks.
Android
для вас подойдут и формат epub и формат fb2. Мы советуем использовать приложения MoonReader , FbReader , EbookReader.
Файлы откроются в этих приложениях, они всегда будут в вашем доступе. Вы сможете настроить визуально текст для своего комфорта.
Если вам привычно читать формат pdf и возникают проблемы, то мы подскажем, как их решить.
Windows
мы советуем формат epub и приложение EbookReader .
Файлы откроются в приложении, будут всегда у вас под рукой, вы также сможете настроить шрифт и яркость.
Если вы предпочитаете читать с экрана компьютера или в распечатанном виде, то рекомендуем скачивать формат pdf.
Для электронных книг мы советуем формат epub или pdf. Вам необходимо будет скачать файлы сначала на Пк, а затем перенести их в память электронной книги через карту памяти или шнур USB.
Видео:Окружность Эйлера (окружность 9 точек) и прямая ЭйлераСкачать

Спасибо!
Письмо с обзором придет на Вашу почту в течение 10 минут. Проверьте папку «Спам» или «Нежелательная почта».
Если письмо так и не пришло — напишите нам на kratko@knigikratko.ru, мы оперативно его продублируем.
Видео:Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Спасибо!
Вы скачали уже три обзора книг. Для вас доступ к дальнейшему скачиванию закрыт. Вы сможете читать обзоры, только оформив подписку.
Видео:Окружность девяти точек уничтожает задачу на ЕГЭСкачать

Спасибо!
В течение пары минут вы получите на свой e-mail письмо с бесплатным обзором.
Видео:#161. САМАЯ КРАСИВАЯ ФОРМУЛА В МАТЕМАТИКЕ — ФОРМУЛА ЭЙЛЕРА: e^(iπ)+1=0Скачать

Спасибо!
С Праздником вас!
Мы отправили вам 3 бесплатных обзора на указанный e-mail. Внимательно проверьте папку «Спам» или «Нежелательные» вашего почтового ящика. Если там все же нет письма с книгами – то пишите нам на kratko@knigikratko.ru – мы оперативно вам их пришлем!
Видео:Теорема Эйлера | Доказательство.Скачать

Заказ подписки
Оставьте ваши данные для оформления подписки.
Видео:Окружность. 7 класс.Скачать

Заказ подписки
Видео:Прямая Эйлера (доказательство)Скачать

Круги Эйлера
Подарок для Вас!
Мы пришлем Вам обзор полезной книги.
Идеальный руководитель Ицхак Адизес
Круги Эйлера представляют собой особую геометрическую схему, необходимую для поиска и более наглядного отображения логических связей между понятиями и явлениями, а также для изображения отношений между определенным множеством и его частью. Благодаря наглядности они значительно упрощают любые рассуждения и помогают быстрее находить ответы на вопросы.
Автором кругов является известный математик Леонард Эйлер, который считал, что они необходимы, чтобы облегчить размышления человека. С момента своего появления метод приобрел широкую популярность и признание.
Позже круги Эйлера использовали в своих работах многие известные ученые, к примеру, чешский математик Бернард Больцано, немецкий математик Эрнест Шредер, английский философ и логик Джон Венн и другие. Сегодня методика служит основной многих упражнений на развитие мышления, в том числе и упражнений из нашей бесплатной онлайн-программы «Нейробика».
Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Для чего нужны круги Эйлера
Круги Эйлера имеют прикладное значение, ведь с их помощью можно решать множество практических задач на пересечение или объединение множеств в логике, математике, менеджменте, информатике, статистике и т.д. Полезны они и в жизни, т.к., работая с ними, можно получать ответы на многие важные вопросы, находить массу логических взаимосвязей.
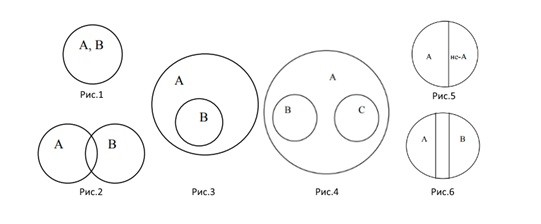
Есть несколько групп кругов Эйлера:
- равнозначные круги (рисунок 1 на схеме);
- пересекающиеся круги (рисунок 2 на схеме);
- подчиненные круги (рисунок 3 на схеме);
- соподчиненные круги (рисунок 4 на схеме);
- противоречащие круги (рисунок 5 на схеме);
- противоположные круги (рисунок 6 на схеме).
Но в упражнениях на развитие мышления чаще всего встречаются два вида кругов:
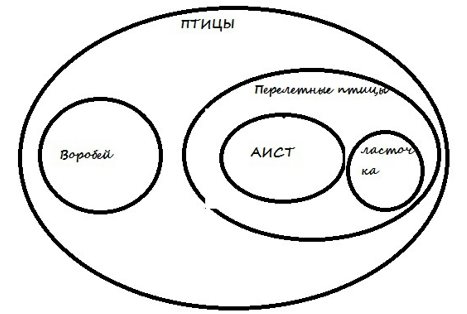
- Круги, описывающие объединения понятий и демонстрирующие вложенность одного в другое. Посмотрите пример:
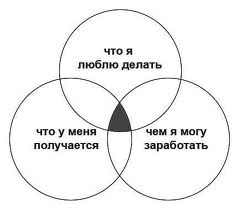
- Круги, описывающие пересечения разных множеств, имеющих некоторые общие признаки. Посмотрите пример:
Результат использования кругов Эйлера проследить на этом примере очень просто: обдумывая, какую профессию выбрать, вы можете либо долго рассуждать, пытаясь понять, что больше подойдет, а можете нарисовать аналогичную диаграмму, ответить на вопросы и сделать логический вывод.
Применять метод очень просто. Также его можно назвать универсальным – подходящим для людей всех возрастов: от детей дошкольного возраста (в детских садах детям преподают круги, начиная с 4-5-летнего возраста) до студентов (задачи с кругами есть, к примеру, в тестах ЕГЭ по информатике) и ученых (круги широко применяются в академической среде).
Видео:#234. Формула Эйлера | Свойства отрезков хорд и секущихСкачать

Типичный пример кругов Эйлера
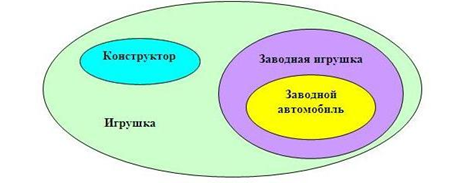
Чтобы вы могли лучше понять, как «работают» круги Эйлера, рекомендуем познакомиться с типичным примером. Обратите внимание на нижеследующий рисунок:
На рисунке зеленым цветов отмечено наибольшее множество, представляющее собой все варианты игрушек. Один из них – это конструкторы (голубой овал). Конструкторы – это отдельное множество само по себе, но в то же время и часть общего множества игрушек.
Заводные игрушки (фиолетовый овал) тоже относятся к множеству игрушек, однако к множеству конструктора они отношения не имеют. Зато заводной автомобиль (желтый овал), пусть и является самостоятельным явлением, но считается одним из подмножеств заводных игрушек.
По подобной схеме строятся и решаются многие задачи (включая и задания на развитие когнитивных способностей), задействующие круги Эйлера. Давайте разберем одну такую задачу (кстати, именно ее в 2011 году внесли на демонстрационный тест ЕГЭ по информатике и ИКТ).
Видео:ЛШУ 2021. Окружность Эйлера. Наталья НетрусоваСкачать

Пример решения задачи с помощью кругов Эйлера
Условия задачи таковы: приведенная таблица показывает, сколько страниц было найдено в Интернете по конкретным запросам:
| Запрос | Найдено страниц (в тысячах) |
| Крейсер/линкор | 7 000 |
| Крейсер | 4 800 |
| Линкор | 4 500 |
Вопрос задачи: сколько страниц (в тысячах) выдаст поисковик по запросу «Крейсер и линкор»? При этом нужно учитывать, что все запросы выполняются примерно в одно и то же время, поэтому набор страниц с искомыми словами со времени выполнения запросов остался неизменным.
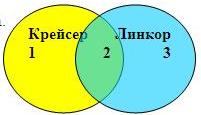
Решается задача так: с помощью кругов Эйлера изображаются условия задачи, а цифрами «1», «2» и «3» обозначаются полученные в результате сегменты:
Учитывая условия задачи, составляем уравнения:
- Крейсер/линкор: 1+2+3 = 7 000;
- Крейсер: 1+2 = 4 800;
- Линкор: 2+3 = 4 500.
Чтобы определить количество запросов «Крейсер и линкор» (сегмент обозначен цифрой «2» на рисунке), подставим в уравнение 1 уравнение 2 и получим:
4 800 + 3 = 7 000, а значит, что 3 = 2 200 (т.к. 7 000-4 800 = 2 200).
Далее полученный результат подставляем в уравнение 3 и получаем:
2 + 2 200 = 4 500, а это означает, что 2 = 2 300 (т.к. 4 500-2 200 = 2 300).
Ответ: по запросу «Крейсер и линкор» будет найдено 2 300 страниц.
Этот пример наглядно демонстрирует, что с помощью кругов Эйлера можно достаточно быстро и просто решать сложные задачи.
Видео:26 Окружность девяти точекСкачать

Резюме
Круги Эйлера – это очень полезная методика решения задач и установления логических связей, а заодно и занимательный и интересный способ провести время и потренировать мозг. Так что, если вам хочется совместить приятное с полезным и поработать головой, предлагаем пройти наш курс «Нейробика», включающий в себя самые разные задания, в том числе и круги Эйлера, эффективность которых научно обоснована и подтверждена многолетней практикой.
В нашей Библиотеке вы можете прочитать обзор по книге Тима Кларка, Александра Остервальдера, Ива Пинье «Твоя бизнес-модель. Системный подход к построению карьеры». Авторы книги предлагают интересное решение: подойти к собственной личности как к проекту и разработать бизнес-модель своей карьеры.
Видео:Окружность и прямая ЭйлераСкачать

Исследовательская работа «Круги Эйлера»
Видео:ТРИГОНОМЕТРИЯ С НУЛЯ - Единичная Окружность // Подготовка к ЕГЭ по МатематикеСкачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»
Свидетельство и скидка на обучение каждому участнику
Именно математика дает
кто им следует – тому не опасен
Уже много лет представителям тех или иных профессий и специальностей нужно решать задачи, связанные с перебором различных комбинаций, составленных из различных объектов.
Эти занимается раздел математики под названием комбинаторика. Отличительный признак комбинаторных задач – это вопрос, который можно сформулировать так: Сколькими различными способами…? Сколько различных вариантов…?
Термин «комбинаторика» происходит от латинского слова «combina», что в переводе на русский означает – «сочетать», «соединять».
Каждый человек применяет в той или иной мере теорию вероятности в своей жизни. Чаще это наши попытки спрогнозировать исход произошедших в нашей жизни событий. Примеров можно привести множество. Люди, например, считают, что вероятность погибнуть в результате автомобильной аварии выше, нежели от удара молнии. Связано это с тем, что первое, к сожалению, просто на просто происходит чаще. Для чего человеку нужно так или иначе определять вероятность происходящих в его жизни событий? Всему причина огромное желание управлять процессами окружающего мира и прогнозировать свое поведение в разных жизненных ситуациях. Всегда ли получается? Конечно нет! Мы не всегда можем в точности определить вероятность протекающих вокруг нас событий.
Приведу еще один печальный пример. Мы склонны почему-то думать, что вероятность смертельного исхода во время авиакатастрофы выше, чем по время автокатастрофы. Это обусловлено тем, что человек просто привык ходить по земле и в воздухе чувствует себя некомфортно. Это все от незнания статистики. Если изучить различные факты и статистику этих процессов, то становится понятно, что мы ошибаемся.
Даже если человек и сможет определить вероятность исхода какого-либо события, то скорее всего не на должном уровне точности. А когда нам нужна точность, то куда мы обращаемся? Конечно же, к математике.
Примеров применения теории вероятностей можно приводить бесконечно. Пытаясь предугадать исход какой–либо операции или процесса, человек применяет ее практически везде. Можно сказать с уверенностью, что вся нынешняя экономика основывается на теории вероятностей и статистике.
Любой предприниматель, исследуя рынок и выдвигая на этот рынок какой-либо товар, обязательно старается учесть риски, рассчитывает вероятность покупки этого товара на разных рынках. Брокеры – официальные участники рынка ценных бумаг, которые участвуют в проведении различных операций на рынке денег, вообще не могут представить себе свою жизнь без теории вероятностей. Предсказывание денежного курса, в котором конечно же не обойтись без теории вероятности, на денежных опционах или рынках позволяет зарабатывать на данной теории немалые деньги.
Теория вероятности имеет огромное значение на начальном этапе планирования любой деятельности, и еще большее значение для регулирования этой деятельности.
Человек пытается оценить все: вероятность выжить в той и ли иной катастрофе, вероятность поломки или неполадки в конструкции самолета или космического корабля, вероятность теракта в метрополитене, вероятность наступления кризиса в стране, вероятность войны и многое другое. И это делается с целью предпринять какие-либо действия исходя из этих данных. Применяя статистику и теорию вероятностей, все риски, описанные выше можно выразить в процентах.
Можно с уверенностью сказать, что любую деятельность можно спланировать, использую статистику, рассчитать благодаря теории вероятности основные риски и благодаря этому, улучшить процесс планирования своей деятельности.
В данной работе рассмотрены основные задачи теории вероятностей, которые можно решить, применяя диаграммы Эйлера. На мой взгляд, применение диаграмм Эйлера дает четкое наглядное представление о самой задаче и ее решении.
Гипотеза исследования: Решение комбинаторных задач и задач теории вероятностей с помощью кругов Эйлера развивает логическое мышление, творческие способности, применяется при решении олимпиадных задач, имеет глубокое практическое применение, а также дает наглядное представление ходе решения задач на основные теоремы теории вероятностей.
Ответом на вопрос, применяется ли теории вероятностей и комбинаторика в реальной жизни, несомненно будет: да!
Цель работы: изучить решение задач теории вероятностей посредством построения кругов (диаграмм) Эйлера.
Уметь составлять и решать задачи с помощью кругов Эйлера;
Выполнить поиск информации в сети Internet;
Применять полученные знания в дальнейшем обучении математике;
Расширить и углубить представление о практическом значении математики в жизни;
Уметь работать с научно-познавательной литературой, анализировать, делать выводы.
Объект исследования : задачи теории вероятностей.
Предмет исследования : диаграммы Эйлера как инструмент для решения задач теории вероятностей.
Методы: отбор источников информации, изучение материала и его анализ.
Актуальность выбранной темы заключается в необходимости решения комбинаторных задач и задач теории вероятностей на уроках математики, так как эти задачи все взяты из нашей реальной жизни. На мой взгляд, задачи реальной математики, должны изучаться и рассматриваться в первую очередь. А вероятностные задачи мы ставим на каждом этапе своей жизни, на каждом этапе создания нового, при расчетах и планировании того, какой шаг сделать следующим.
Теория множеств и диаграммы Эйлера.
Вначале необходимо сказать конечно немного о множествах. С множествами я познакомился еще вначале учебы в школе. Слово множество, являясь основным понятием математики, не имеет своего определения. Можно сказать, что это какие-либо объекты или явления, которые мы объединяем в целое, учитывая их общие признаки. Этот общий признак называют характеристическим. Множеством можно назвать любой набор, группу, совокупность. Это множество натуральных чисел, множество особей, множество формул механики, множество птиц, множество учащихся класса и так далее.
Существует следующие основные виды множеств:
Заданное множество – множество, в котором о любом его элементе можно сказать принадлежит оно этому множеству или нет.
Пустое множество – множество, которое не содержит элементов и обозначается символом .
Конечное множество – множество, которое содержит определенное число элементов.
Бесконечное множество – множество, содержащее неограниченное число n(A) элементов.
Равные множества – множества, состоящие из одних и тех же элементов.
Подмножеством множества В является множество А при условии, что любой элемент этого множества А также является элементом множества В. Пустое множество является подмножеством любого множества.
Например, есть множество учеников 8 «м» класса. Девочки 8 «м» класса образуют подмножество учеников 8 «м». Множества мальчиков и девочек 8 «м» не пересекаются. Но если рассмотреть множество учеников 8 «м», посещающих кружок по математике и множество учеников 8 «м», посещающих кружок по футболу, то такие множества могут пересекаться, а в случае моего 8 «м» класса они пересекаются, так как три ученика нашего класса посещают оба кружка.
Нет ученого, имя которого упоминалось бы в учебной литературе по математике столь же часто, как имя Эйлера. В Энциклопедии можно найти сведения о шестнадцати формулах, уравнениях, теоремах и т. д., носящих имя Эйлера. (ссылка)
Круги Эйлера – это определенная геометрическая схема, которая делает более наглядными логические связи между различными явлениями и понятиями, также позволяет продемонстрировать связь между каким-либо множеством и его подмножествами, а также дает четкое наглядное представление о пересечении множеств.
Этот метод даёт ещё более наглядное представление о возможном способе изображения условий, зависимости, отношений в логических задачах. Множество всех действительных чисел Эйлер изобразил с помощью этих кругов: N-множество натуральных чисел, Z – множество целых чисел, Q – множество рациональных чисел, R – множество вех действительных чисел.
В качестве примера, рассмотрим простенькую распространенную олимпиадную задачу, составленную нами:
«В магазине побывало 65 человек. Известно, 35 из них купили масло, 36 — хлеб, 37 – рис. 20 из них купили и масло и хлеб, 19 — и хлеб и рис, 15 — масло и рис, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего?»
И вот решение с применением диаграмм Эйлера:
Решение задач теории вероятностей с применением диаграмм Эйлера
По отзывам покупателей Магомед Ахмедович оценил надёжность двух интернет-магазинов. Вероятность того, что нужный товар доставят из магазина I , равна 0,7. Вероятность того, что этот товар доставят из магазина II , равна 0,8. Магомед Ахмедович заказал товар сразу в обоих магазинах. Считая, что интернет-магазины работают независимо друг от друга, найдите вероятность того, что ни один магазин не доставит товар.
Решение: Вероятность того, что первый магазин не доставит нужный товар равна 1 − 0,7 = 0,3. Вероятность того, что второй магазин не доставит нужный товар равна 1 − 0,8 = 0,2.
Первый Оба Второй
магазин магазина магазин
не доставит товар не доставят товар не доставит товар
Первый доставит 0,7 Оба доставят 0,56 Второй доставит 0,8
Вероятность наступления обоих событий есть вероятность произведения этих событий. Вероятность произведения событий есть произведение вероятностей двух событий. Ответ: 0,06.
В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,2. Вероятность того, что кофе закончится в обоих автоматах, равна 0,14. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.
Кофе закончится Кофе Кофе закончится
в I автомате закончится во II автомате
P ( A ) = 0,2 в обоих автоматах P ( B )= 0,2
закончится в обоих автоматах
А- кофе закончится в I автомате
В — кофе закончится во II автомате
А+В – кофе закончится хотя бы в одном автомате
АВ – кофе закончится в обоих автоматах
С – кофе останется в обоих автоматах (кофе не закончится в обоих автоматах)
По диаграмме видно, что событие «Кофе не закончится» противоположно событию «Кофе закончится хотя бы в одном автомате» противоположны и их сумма составляет 1. Когда мы ищем вероятность события «Кофе закончится хотя бы в одном автомате» как сумму вероятностей событий «Кофе закончится в I автомате» и «Кофе закончится во II автомате», то по диаграмме четко и наглядно видно, что вероятность совместного наступления этих событий складывается дважды. Потому нужно из этой суммы вычесть вероятность совместного наступления событий «Кофе закончится в обоих автоматах».
Отсюда и формула
Р (С)=1- Р (А+В)= 1-0,26 =0,74
На экзамене по истории ученик должен ответить на один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос по теме «Японская война», равна 0,4. Вероятность того, что это вопрос по теме «Великая Отечественная война», равна 0,25. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
«Японская война» «Великая Отечественная война»
Данные множества не пересекаются, так как нет, по условию задачи, вопросов, относящихся одновременно к обеим темам. Потому вероятность события «Достанется вопрос хотя бы по одной из этих двух тем» равна сумме вероятностей каждого события. Ответ: 0,65.
Помещение освещается фонарём с тремя лампами. Вероятность перегорания лампы в течение года равна 0,2. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит.
Перегорит Перегорят Перегорит
первая лампа все лампы вторая лампа
Перегорит третья лампа
Не перегорит ни одна лампа
Понятно, что событие «Хотя бы одна лампа не перегорит» противоположно событию перегорят все три лампы и есть сумма событий «Не перегорит первая лампа», «Не перегорит вторая лампа», «Не перегорит третья лампа», «Не перегорит ни одна лампа». Но тут проще найти вероятность перегорания трех ламп и определить разность единицы и полученного значения вероятности.
А – событие «Перегорит одна лампа»
В – событие «Перегорит вторая лампа»
С – событие «Перегорит третья лампа»
А В C – событие «Перегорят все лампы»
D – событие «Ни одна лампа не перегорит»
Р( D ) = 1 — Р(А)Р(В) Р (С)= 1-0,008 = 0,992
Применение кругов Эйлера (диаграмм Эйлера-Венна) позволяет легко решить задачи, которые обычным путем разрешимы лишь при составлении системы из нескольких уравнений с несколькими неизвестными.
Метод кругов Эйлера позволяет сделать решение задач теории вероятностей более наглядным и понятным, а также понять смысл самих теорем сложения и умножения вероятностей.
В результате исследования рассмотрены основные прототипы задач ЕГЭ по теоремам теории вероятностей и установлено, что при решении таких задач удобно пользоваться методом диаграмм Эйлера.
🎦 Видео
Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать