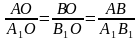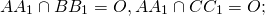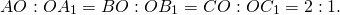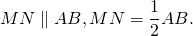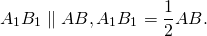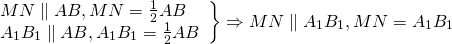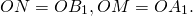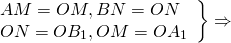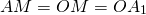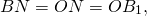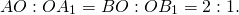Просмотр содержимого документа
«Билет 1, 2 изученое»
1 вопрос: дайте определение многоугольника, вершины, стороны, диагонали и периметра многоугольника. Запишите формулу суммы углов выпуклого многоугольника.
Определение. Многоугольником называют фигуру, составленную из отрезков так, что:
смежные отрезки не лежат на одной прямой
несмежные не имеют общих точек
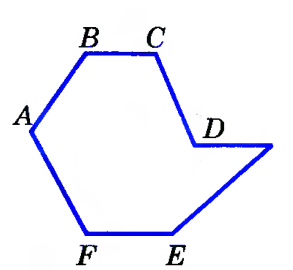
Вершинами называются точки: А, В, С, D, E, F.
Сторонами многоугольника называются отрезки: AB, BC, CD, DE, ЕF, FA.
Диагональю многоугольника называется отрезок, соединяющий две любые не соседние вершины.
Периметром многоугольника называется сумма длин всех сторон.
Сумма углов выпуклого многоугольника равна (n-2) 
2 вопрос: докажите теорему о средней линни
4 вопрос: периметр прямоугольника равен 56, а диагональ равна 20. Найдите площадь этого прямоугольника.
1 вопрос: дайте определение и свойства параллелограмма.
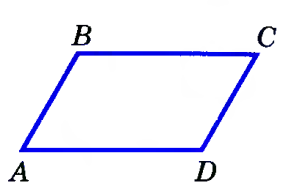
Определение. Параллелограмм – это четырехугольник, у которого противоположные стороны попарно – параллельны.
1° В параллелограмме противоположные углы равны. В параллелограмме противоположные стороны равны.
2° Диагонали параллелограмма точкой пересечения делится пополам.
3° В параллелограмме сумма углов прилежащих к одной стороне равна 180°.
4° Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник.
2 вопрос: доказать свойство медиан треугольника
Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от вершины
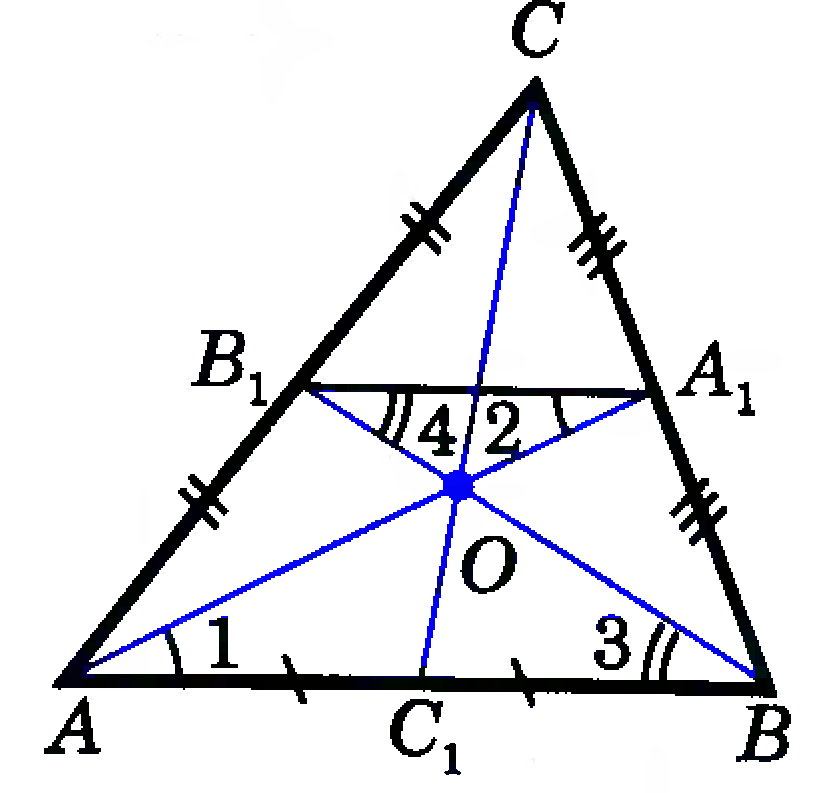
Дано: ∆АВС, О — точка пересечения медиан АА₁ и ВВ₁; А₁В₁ — средняя линия ∆АВС.
Доказать: точка О пересечение медиан АА₁ и ВВ₁ делит каждую из них в отношении 2:1, считая от вершины.
Отрезок А₁В₁ параллелен стороне АВ, поэтому 
Следовательно, треугольники АОВ и А₁ОВ₁ подобны по двум углам, и, значит, их стороны пропорциональны:
Но АВ=2 А₁В₁, поэтому АО=2 

Таким образом, точка О пересечение медиан АА₁ и ВВ₁ делит каждую из них в отношении 2:1, считая от вершины.
Аналогично доказывается, что точка пересечения медиан ВВ₁ и СС₁ делит каждую из них в отношении 2:1, считая от вершины, и, следовательно, совпадает с точкой О.
Итак, все три медианы треугольника АВС пересекаются в точке О и делятся ею в отношении 2:1, считая от вершины.
Видео:Теорема о точке пересечения медиан треугольника. Доказательство. 8 класс.Скачать

Медиана треугольника
Определение . Медианой треугольника называют отрезок, соединяющий вершину треугольника с серединой противоположной стороны (рис 1).
Поскольку в каждом треугольнике имеется три вершины, то в каждом треугольнике можно провести три медианы.
На рисунке 1 медианой является отрезок BD .
Утверждение 1 . Медиана треугольника делит его на два треугольника равной площади ( равновеликих треугольника).
Доказательство . Проведем из вершины B треугольника ABC медиану BD и высоту BE (рис. 2),
и заметим, что (см. раздел нашего справочника «Площадь треугольника»)
Поскольку отрезок BD является медианой, то
что и требовалось доказать.
Утверждение 2 . Точка пересечения двух любых медиан треугольника делит каждую из этих медиан в отношении 2 : 1 , считая от вершины треугольника.
Доказательство . Рассмотрим две любых медианы треугольника, например, медианы AD и CE , и обозначим точку их пересечения буквой O (рис. 3).
Обозначим середины отрезков AO и CO буквами F и G соответственно (рис. 4).
Теперь рассмотрим четырёхугольник FEDG (рис. 5).
Сторона ED этого четырёхугольника является средней линией в треугольнике ABC . Следовательно,
Сторона FG четырёхугольника FEDG является средней линией в треугольнике AOC . Следовательно,
Отсюда вытекает, что точка O делит каждую из медиан AD и CE в отношении 2 : 1 , считая от вершины треугольника.
Следствие . Все три медианы треугольника пересекаются в одной точке.
Доказательство . Рассмотрим медиану AD треугольника ABC и точку O , которая делит эту медиану в отношении 2 : 1 , считая от вершины A (рис.7).
Поскольку точка, делящая отрезок в заданном отношении, является единственной, то и другие медианы треугольника будут проходить через эту точку, что и требовалось доказать.
Определение . Точку пересечения медиан треугольника называют центроидом треугольника.
Утверждение 3 . Медианы треугольника делят треугольник на 6 равновеликих треугольников (рис. 8).
Доказательство . Докажем, что площадь каждого из шести треугольников, на которые медианы разбивают треугольник ABC , равна 
Видео:№110. Докажите, что если медиана треугольника совпадает с его высотой, то треугольникСкачать

Свойство медиан треугольника
Свойство медиан треугольника может быть доказано многими способами. Доказательство, опирающееся на свойства параллелограмма и средней линии треугольника, может быть проведено сразу же после изучения соответствующих тем, что позволяет начать использовать свойство медиан треугольника уже с начала 8 класса.
(Свойство медиан треугольника)
Медианы треугольника пересекаются и в точке пересечения делятся в отношении 2:1, считая от вершины.


(то есть AM=OM, BN=ON).
2) Соединим точки M, N, A1 и B1 отрезками.
3) Так как AA1 и BB1 — медианы треугольника ABC, точка A1- середина отрезка BC, B1 — середина AC.
Следовательно, A1B1 — средняя линия треугольника ABC и
Значит, четырёхугольник MNA1B1 — параллелограмм (по признаку).
По свойству диагоналей параллелограмма
из чего следует, что
5) Доказательство того факта, что все медианы треугольника пересекаются в одной точке, будем вести методом от противного.
Предположим, что третья медиана CC1 треугольника ABC пересекает медианы AA1 и BB1 в некоторой точке, отличной от точки O.
Тогда на каждой медиане есть две различные точки, делящие её в отношении 2:1, считая от вершины. Пришли к противоречию.
Таким образом, все три медианы треугольника пересекаются в одной точке и точка пересечения медиан делит каждую из их в отношении 2:1, считая от вершины:
Что и требовалось доказать .
Видео:Свойство биссектрисы треугольника с доказательствомСкачать

7 Comments
Промогите пожалуйста:
В прямоугольном треугольнике из вершины прямого угла до гипотенузы провели медиану длинной 50см и перпендикуляр 48см. Вычислить периметр.
Медиана, проведённая к гипотенузе, равна её половине. Следовательно, гипотенуза 100 см. Пусть катеты равны x см и y см. По теореме Пифагора x²+y²=100². Площадь треугольника равна половине произведения стороны на высоту, проведённую к этой стороне S=0,5∙100∙48 см², либо половине произведения катетов S=0,5∙x∙y. Отсюда xy=4800.
Решаем систему уравнений: x²+y²=100²; xy=4800. Решения (60;80) (80;60). То есть катеты 60 см и 80 см. Периметр P=60+80+100=240 см.
(Не обязательно доводить решение системы до конца. Достаточно найти x+y. Для этого к 1-му уравнению прибавим удвоенное 2-е, получим
x²+2xy+y²=19600; x+y=140).
Прошу помощи в решении задачи: на стороне ромба построен равносторонний треугольник. Отрезок, соединяющий точку пересечения диагоналей ромба с серединой стороны треугольника, составляет с ней угол 70 градусов. Найти острый угол ромба.
Во-первых, большое спасибо за решение, даже не ожидала ответа, но, по счастью, ошиблась! Но я к этому времени уже решила так:провела ВМ, которая в равностороннем треугольнике является также высотой.
Рассмотрим четырехугольник ОВМС: угол ВОС =углу ВМС=90 градусов (диагонали ромба взаимно перпендикулярны),отсюда, ВМ параллельна ОС, тогда угол МОС=20 градусам. Рассм. треугольник ОМС: угол МСО= 180-20-70=90 градусов, и одновременно= 60+x, т.о., угол х=30 градусам, и искомый острый угол ромба=60 градусам. Мы получили разные ответы, в чем может быть дело (окружности мы еще не проходили).
Наталия углы BOC и BMC не накрест лежащие и не внутренние односторонние, поэтому BM не параллельна OC. Но вариант решения без окружности возможен, добавила второй способ.
🎥 Видео
Высота, биссектриса, медиана. 7 класс.Скачать

№366. Докажите, что если М — точка пересечения медиан треугольника ABC, а О — произвольная точкаСкачать

ГЕОМЕТРИЯ 7 класс. Медиана прямоугольного треугольника. Свойство. Доказательство для 7 класса.Скачать

Точка пересечения медиан в треугольникеСкачать

🔥 Свойства МЕДИАНЫ #shortsСкачать

Доказать, что медиана, проведенная к гипотенузе, равна половине гипотенузыСкачать

Теорема о свойстве медианы равнобедренного треугольникаСкачать
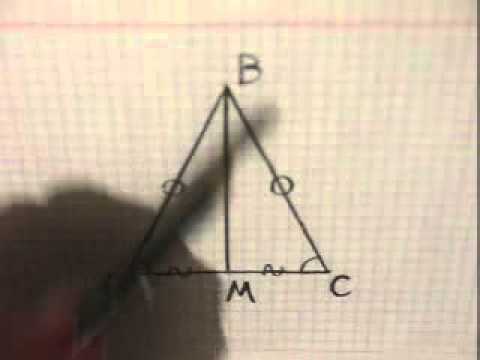
8. Медиана треугольника и её свойства.Скачать

Теорема о трёх медианахСкачать

Урок 33. Свойство медиан треугольника (8 класс)Скачать

Равнобедренный треугольник. Определение. Свойства. Теоремы и доказательства.Скачать

7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

22 Медианы треугольника пересекаются в одной точкеСкачать

7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать

Свойства прямоугольного треугольника. 7 класс.Скачать

Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Свойство медианы в прямоугольном треугольнике. 8 класс.Скачать