Докажите что треугольник авс прямоугольный

теория по математике 📈 планиметрия

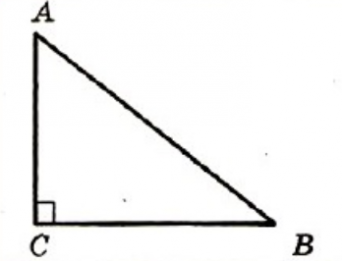
Если в треугольнике есть угол, равный 90 градусов, то такой треугольник называется прямоугольным. Стороны прямоугольного треугольника называются – катеты и гипотенуза. Катеты – это стороны, образующие прямой угол. Гипотенуза – сторона, которая располагается напротив прямого угла.

На рисунке треугольник АВС – прямоугольный, угол С равен 90º, стороны АС и ВС – катеты, а сторона АВ – гипотенуза.

Видео:№199. Прямая р параллельна стороне АВ треугольника ABC. Докажите, что прямые ВССкачать

Свойства прямоугольного треугольника

• В прямоугольном треугольнике гипотенуза является наибольшей стороной.
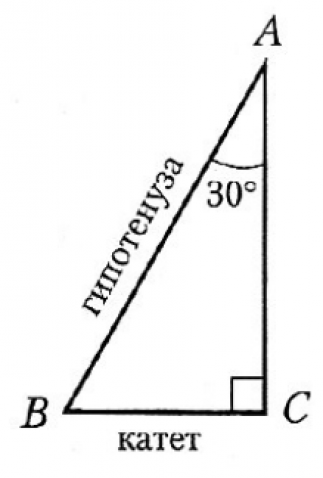
• В прямоугольном треугольнике катет, лежащий напротив угла 30 0 , равен половине гипотенузы. И обратно, если катет равен половине гипотенузы, то угол, лежащий напротив этого катета, равен 30 0 .

Например, пусть угол А=30 0 , а гипотенуза АВ=28 см, то катет ВС будет равен 14 см, так как лежит напротив угла А=30 0 . Или, например, если катет ВС=6 см, а гипотенуза АВ равна 12 см, то угол А (лежащий напротив катета ВС), равен 30 0 .

• Сумма острых углов прямоугольного треугольника равна всегда 90 градусов.
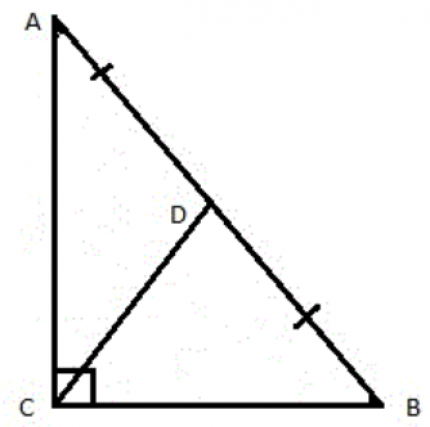
• Медиана, проведенная к гипотенузе, равна её половине.

На рисунке изображен прямоугольный треугольник АВС, где CD – медиана, проведенная к гипотенузе. По свойству – медиана CD=0,5АВ, то есть AD=DB=CD.

Видео:№145. Через вершину А прямоугольного треугольника ABC с прямым углом С проведена прямая AD,Скачать

Признаки равенства прямоугольных треугольников

Существует 4 признака равенства прямоугольных треугольников:

1. Если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны.
2. Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и острому углу другого прямоугольного треугольника, то такие треугольники равны.
3. Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны.
4. Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны.

Чтобы быстрее запомнить данные признаки, можно использовать их краткую трактовку:

1. по катетам;
2. по катету и прилежащему острому углу;
3. по гипотенузе и острому углу;
4. по гипотенузе и катету.

Видео:№231. Медиана AM треугольника ABC равна половине стороны ВС. Докажите, что треугольникСкачать

Теорема Пифагора

Древнегреческий философ, ученый, математик – Пифагор Самосский вывел теорему, которая до сих применима для решения задач. Теорема названа в честь него – «теорема Пифагора».

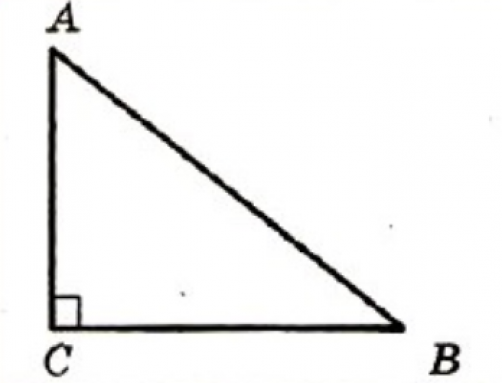
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

На рисунке в прямоугольном треугольнике АВ 2 =АС 2 +ВС 2

Например, если в данном треугольнике катеты равны 9 и 12 см, то можно найти длину гипотенузы, используя теорему: АВ 2 =9 2 +12 2 =81+144=225=15 2 , значит АВ=15 см.

Египетский треугольник

Треугольник со сторонами 3, 4 и 5 см называют Египетским треугольником.

Пифагоровы тройки

Тройки чисел, которые удовлетворяют теореме Пифагора, называют Пифагоровы тройки, а сами числа – Пифагоровы числа. Например, такими являются числа 16, 12 и 20 – это числа, которые при подстановке в формулу теоремы, дают нам верное равенство: 16 2 +12 2 =20 2 , 256+144=400, 400=400.

Видео:№269. Докажите, что ΔАВС=ΔА1B1С1, если ∠A=∠A1, ∠B=∠B1 и ВН=В1Н1, где ВН и В1Н1Скачать

Медиана AM треугольника ABC равна половине стороны ВС. Докажите, что треугольник ABC прямоугольный

Видео:Геометрия 7 класс (Урок№25 - Прямоугольные треугольники.)Скачать

Ваш ответ

Видео:№170. Докажите, что треугольники ABC и А1B1С1 равны, если АВ =А1В1, ∠A=∠A1, AD =A1D1, где AD и A1D1Скачать

решение вопроса

Видео:№110. Докажите, что если медиана треугольника совпадает с его высотой, то треугольникСкачать

Похожие вопросы

• Все категории
• экономические 43,283
• гуманитарные 33,619
• юридические 17,900
• школьный раздел 607,084
• разное 16,829

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:Признаки равенства треугольников. 7 класс.Скачать

Докажите что треугольник авс прямоугольный

Доказать, что треугольник с вершинами A(-3, -2), B(0, -1) и C(-2, 5) прямоугольный.

Известно, что треугольник является прямоугольным, если квадрат большей из его сторон равен сумме квадратов двух других сторон.

Найдем длины сторон нашего треугольника. Воспользуемся формулой

Подставляя в данную формулу исходные данные, находим длины сторон треугольника AB, BC и AC:

Из полученных данных нетрудно заметить, что квадрат наибольшей стороны AC действительно равен сумме двух других сторон.

📺 Видео

Равнобедренный треугольник. 7 класс.Скачать

№147. Из точки М проведен перпендикуляр МВ к плоскости прямоугольника ABCD. Докажите, чтоСкачать

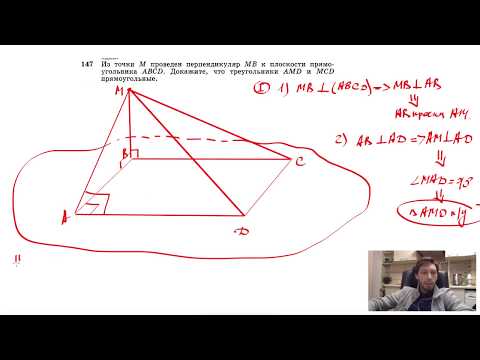
№412. Даны равнобедренный прямоугольный треугольник ABC с прямым углом С, катетом АС = 12 смСкачать

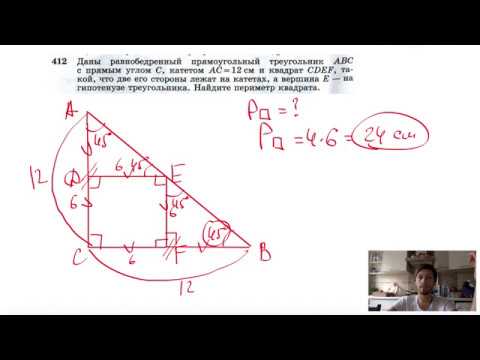
Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

№947. Докажите, что треугольник ABC равнобедренный, и найдите его площадь, если вершины треугольникаСкачать

Признаки равенства треугольников. Практическая часть. 7 класс.Скачать

Геометрия 7 класс (Урок№15 - Решение задач на признаки равенства треугольников.)Скачать

7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать

7 кл г. Теорема: «катет лежавший напротив угла в 30 градусов равен половине гипотенузы»Скачать

№21. Треугольники ABC и ABD не лежат в одной плоскости. Докажите,Скачать

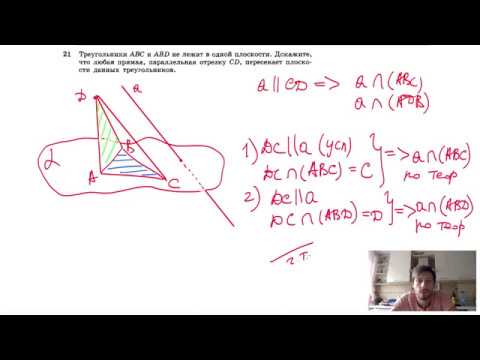
7 класс, 36 урок, Признаки равенства прямоугольных треугольниковСкачать