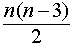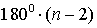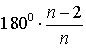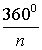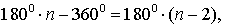Определение. Внешним углом треугольника называется угол, смежный к любому углу этого треугольника.
 |
На Рис.1 угол 4 внешний так как углы 2 и 4 смежные.
Теорема. Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.
Доказательство. Докажем, что ( small angle 4=angle 1+ angle 3. ) Поскольку сумма углов треугольника равна 180°, то имеем:
- Внешний угол треугольника доказательство
- Многоугольники
- Определение многоугольника
- Диагонали n — угольника
- Внешний угол многоугольника
- Свойства углов треугольника
- Свойства углов многоугольника
- Свойства углов правильного n – угольника
- Доказательства свойств углов многоугольника
- Внешний угол треугольника
- Внешний угол треугольника
- Сумма внешних углов
- Внешний угол треугольника
- Сумма внешних углов
Внешний угол треугольника доказательство
Многоугольники
 Определение многоугольника |
| Диагонали n – угольника |
| Внешний угол многоугольника |
| Свойства углов треугольника |
| Свойства углов многоугольника |
| Свойства углов правильного n – угольника |
| Доказательства теорем о свойствах углов многоугольника |
Определение многоугольника
Рассмотрим n отрезков
| [A1 A2], [A2 A3], … , [An An +1] | (1) |
причём таких, что два любых отрезка, имеющих общий конец, не лежат на одной прямой (рис.1).
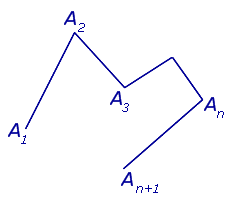
Определение 1 . Ломаной линией с n звеньями называют фигуру L , составленную из отрезков (1), то есть фигуру, заданную равенством
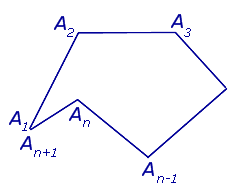
В случае, когда точки A1 и An +1 совпадают, ломаную линию называют замкнутой ломаной линией (рис. 2), в противном случае её называют незамкнутой (рис.1).
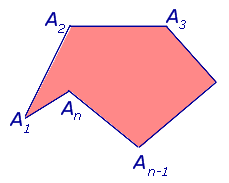
Определение 2 . Многоугольником называют часть плоскости, ограниченную замкнутой ломаной линией без самопересечений (рис. 3). Отрезки, составляющие ломаную линию ( звенья ), называют сторонами многоугольника. Концы отрезков называют вершинами многоугольника.
Определение 3 . Многоугольник называют n – угольником , если он имеет n сторон.
Таким образом, многоугольник, имеющий 3 стороны, называют треугольником , многоугольник, имеющий 4 стороны, называют четырёхугольником и т.д.
Определение 4 . Периметром многоугольника называют сумму длин всех сторон многоугольника.
Величину, равную половине периметра, называют полупериметром .
Диагонали n — угольника
| Фигура | Рисунок | Описание |
| Диагональ многоугольника | 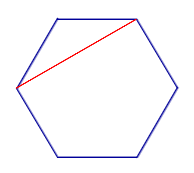 | Диагональю многоугольника называют отрезок, соединяющий две несоседние вершины многоугольника |
| Диагонали n – угольника, выходящие из одной вершины | 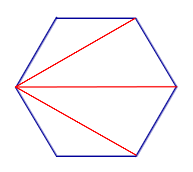 | Диагонали, выходящие из одной вершины n – угольника, делят n – угольник на n – 2 треугольника |
| Все диагонали n – угольника |  |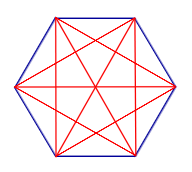
Число диагоналей n – угольника равно
| Диагональ многоугольника |
|
Диагональю многоугольника называют отрезок, соединяющий две несоседние вершины многоугольника
Диагонали, выходящие из одной вершины n – угольника, делят n – угольник на n – 2 треугольника
Число диагоналей n – угольника равно
Внешний угол многоугольника
Определение 5 . Два угла называют смежными , если они имеют общую сторону, и их сумма равна 180° (рис.1).
Определение 6 . Внешним углом многоугольника называют угол, смежный с внутренним углом многоугольника (рис.2).
Свойства углов треугольника
| Фигура | Рисунок | Формулировка теоремы |
| Углы треугольника |  |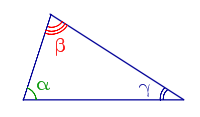
Сумма углов треугольника равна 180°
Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним
| Углы треугольника |
|
Сумма углов треугольника равна 180°
Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним
Свойства углов многоугольника
| Фигура | Рисунок | Формулировка теоремы |
| Углы n – угольника |  |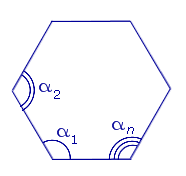
Сумма углов многоугольника равна
n – угольника
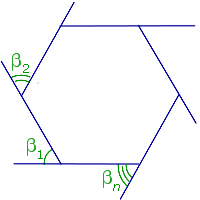
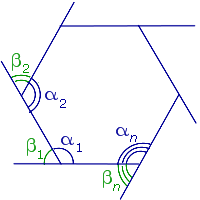
Сумма внешних углов n – угольника, взятых по одному у каждой вершины, равна 360°
| Углы n – угольника |
|
Сумма углов многоугольника равна
Сумма внешних углов n – угольника, взятых по одному у каждой вершины, равна 360°
Свойства углов правильного n – угольника
| Фигура | Рисунок | Формулировка теоремы |
| Углы правильного n – угольника |  |
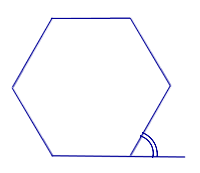
Все углы правильного n – угольника равны
правильного
n – угольника
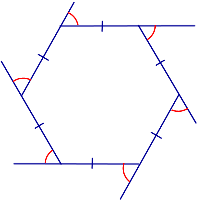
Все внешние углы правильного
n – угольника равны
| Углы правильного n – угольника |
|
Все углы правильного n – угольника равны
Все внешние углы правильного
n – угольника равны
Доказательства свойств углов многоугольника
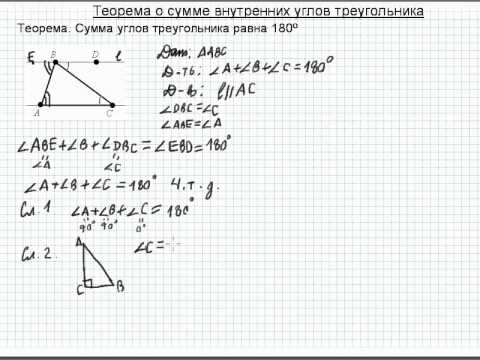
Теорема 1 . В любом треугольнике сумма углов равна 180° .
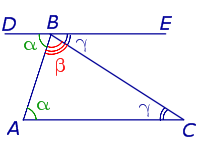
Доказательство . Проведем, например, через вершину B произвольного треугольника ABC прямую DE, параллельную прямой AC, и рассмотрим полученные углы с вершиной в точке B (рис. 3).
Углы ABD и BAC равны как внутренние накрест лежащие. По той же причине равны углы ACB и CBE . Поскольку углы ABD , ABC и CBE в сумме составляют развёрнутый угол, то и сумма углов треугольника ABC равна 180° . Теорема доказана.
Теорема 2 . Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.
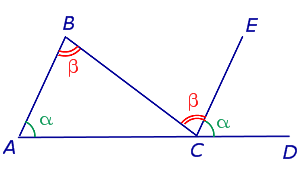
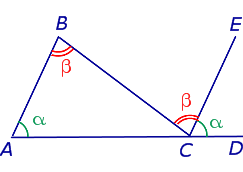
Доказательство . Проведём через вершину C прямую CE, параллельную прямой AB, и продолжим отрезок AC за точку C (рис.4).
Углы ABC и BCE равны как внутренние накрест лежащие. Углы BAC и ECD равны как соответственные равны как соответственные . Поэтому внешний угол BCD равен сумме углов BAC и ABC . Теорема доказана.
Замечание . Теорема 1 является следствием теоремы 2.
Теорема 3 . Сумма углов n – угольника равна
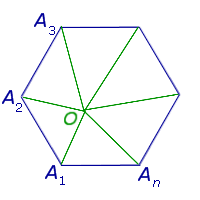
Доказательство . Выберем внутри n – угольника произвольную точку O и соединим её со всеми вершинами n – угольника (рис. 5).
Получим n треугольников:
Сумма углов всех этих треугольников равна сумме всех внутренних углов n – угольника плюс сумма всех углов с вершиной в точке O . Поэтому сумма всех углов n – угольника равна
что и требовалось доказать.
Теорема 4 . Сумма внешних углов n – угольника, взятых по одному у каждой вершины, равна 360° .
Доказательство . Рассмотрим рисунок 6.
В соответствии рисунком 6 справедливы равенства
Внешний угол треугольника
Определение. Внешним углом треугольника называется угол, смежный к любому углу этого треугольника.
|
На Рис.1 угол 4 внешний так как углы 2 и 4 смежные.
Теорема. Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.
Доказательство. Докажем, что ( small angle 4=angle 1+ angle 3. ) Поскольку сумма углов треугольника равна 180°, то имеем:
Внешний угол треугольника
Внешний угол треугольника — это угол, смежный с любым из внутренних углов треугольника.
При каждой вершине треугольника может быть построено по два равных внешних угла. Например, если продолжить все стороны треугольника ABC, то при каждой его вершине получится по два внешних угла, которые равны между собой, как вертикальные углы:
Из данного примера можно сделать вывод, что внешние углы, построенные при одной вершине, будут равны.
Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.
Так как внешний угол (∠1) дополняет внутренний угол (∠4) до развёрнутого угла, то их сумма равна 180°:
Сумма внутренних углов углов любого треугольника тоже равна 180°, значит:
Из этого следует, что
Сократив обе части полученного равенства на одно и тоже число (∠4), получим:
Из этого можно сделать вывод, что внешний угол треугольника всегда больше любого внутреннего угла, не смежного с ним.
Сумма внешних углов
Сумма трёх внешних углов треугольника, построенных при разных вершинах, равна 360°
Рассмотрим треугольник ABC:
Каждая пара углов (внутренний и смежный с ним внешний) в сумме равны 180°. Все шесть углов (3 внутренних и 3 внешних) вместе равны 540°:
(∠1 + ∠4) + (∠2 + ∠5) + (∠3 + ∠6) = 180° + 180° + 180° = 540°.
Значит чтобы найти сумму внешних углов, надо из общей суммы вычесть сумму внутренних углов:
∠1 + ∠2 + ∠3 = 540° — (∠4 + ∠5 + ∠6) = 540° — 180° = 360°.
Внешний угол треугольника
Внешний угол треугольника — это угол, смежный с любым из внутренних углов треугольника.
При каждой вершине треугольника может быть построено по два равных внешних угла. Например, если продолжить все стороны треугольника ABC, то при каждой его вершине получится по два внешних угла, которые равны между собой, как вертикальные углы:
Из данного примера можно сделать вывод, что внешние углы, построенные при одной вершине, будут равны.
Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.
Так как внешний угол (∠1) дополняет внутренний угол (∠4) до развёрнутого угла, то их сумма равна 180°:
Сумма внутренних углов углов любого треугольника тоже равна 180°, значит:
Из этого следует, что
Сократив обе части полученного равенства на одно и тоже число (∠4), получим:
Из этого можно сделать вывод, что внешний угол треугольника всегда больше любого внутреннего угла, не смежного с ним.
Сумма внешних углов
Сумма трёх внешних углов треугольника, построенных при разных вершинах, равна 360°
Рассмотрим треугольник ABC:
Каждая пара углов (внутренний и смежный с ним внешний) в сумме равны 180°. Все шесть углов (3 внутренних и 3 внешних) вместе равны 540°:
(∠1 + ∠4) + (∠2 + ∠5) + (∠3 + ∠6) = 180° + 180° + 180° = 540°.
Значит чтобы найти сумму внешних углов, надо из общей суммы вычесть сумму внутренних углов:
∠1 + ∠2 + ∠3 = 540° — (∠4 + ∠5 + ∠6) = 540° — 180° = 360°.