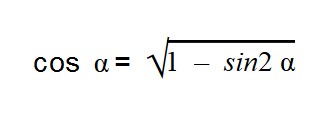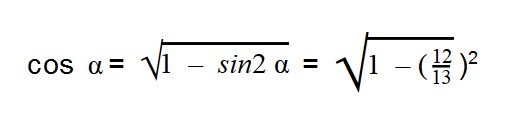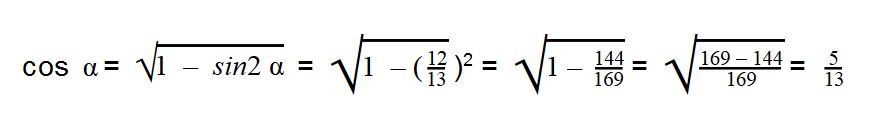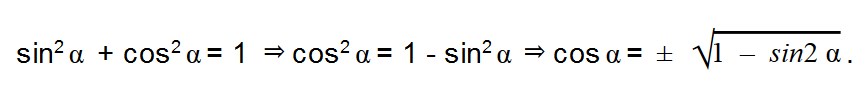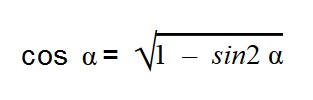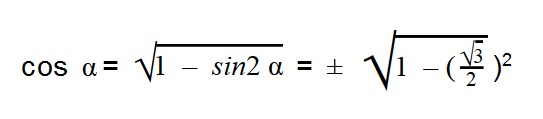О чем эта статья:
9 класс, 10 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
- Связь между sin и cos одного угла
- Тангенс и котангенс через синус и косинус
- Связь между тангенсом и котангенсом
- Тангенс и косинус, котангенс и синус
- Примеры решения задач
- Основные тригонометрические тождества: их формулировки и вывод
- Связь между sin и cos одного угла
- Тангенс и котангенс через синус и косинус
- Связь между тангенсом и котангенсом
- Тангенс и косинус, котангенс и синус
- Please wait.
- We are checking your browser. mathvox.ru
- Why do I have to complete a CAPTCHA?
- What can I do to prevent this in the future?
- 📽️ Видео
Видео:Доказательство основного тригонометрического тождества (видео 1)|Тригонометрия | МатематикаСкачать

Связь между sin и cos одного угла
Вы уже наверняка знаете, что тождественный — это равный.
Основные тригонометрические тождества — это равенства, которые устанавливают связь между синусом, косинусом, тангенсом и котангенсом одного угла. Это значит, что любую из этих функций можно найти, если известна другая функция.
Ключ к сердцу тригонометрии — основное тригонометрическое тождество. Запомните и полюбите его, чтобы отношения с тригонометрией сложились самым наилучшим образом:
sin 2 α + cos 2 α = 1
Из основного тождества вытекают равенства тангенса и котангенса, поэтому оно — ключевое.
Равенство tg 2 α + 1 = 1/cos 2 α и равенство 1 + сtg 2 α + 1 = 1/sin 2 α выводят из основного тождества, разделив обе части на sin 2 α и cos 2 α.
В результате деления получаем:
Поэтому основному тригонометрическому тождеству уделяется максимум внимания. Но какая же «метрия» может обойтись без доказательств. Видите тождество — доказывайте, не раздумывая.
sin 2 α + cos 2 α = 1
Сумма квадратов синуса и косинуса одного угла тождественно равна единице.
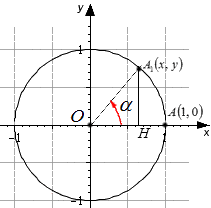
Чтобы доказать тождество, обратимся к теме единичной окружности.
Единичная окружность — это окружность с центром в начале прямоугольной декартовой системы координат. Радиус единичной окружности равен единице.
Докажем тождество sin 2 α + cos 2 α = 1
- Итак, нам известны координаты точки A (1; 0).
Произвольный угол α, тогда cos α = x0 = ОB.
- Синус угла (sin α) — это отношение противолежащего катета к гипотенузе.
- Косинус угла (cos α) — это отношение прилежащего катета к гипотенузе.
Это значит, что точка A1 получает координаты cos α, sin α.
Образовался прямоугольный треугольник OA1B.
|OB| = |x|.
Гипотенуза OA1 имеет значение, равное радиусу единичной окружности.
|OA1| = 1.
Применяя полученное выражение, записываем равенство по теореме Пифагора, поскольку получившийся угол — прямой:
|A1B| 2 + |OB| 2 = |OA1| 2 .
Записываем в виде: |y| 2 + |x| 2 = 1 2 .
Это значит, что y 2 + x 2 = 1.
sin угла α = y
cos угла α = x
Вставляем данные угла вместо координат точек:
OB = cos α
A1B = sin α
A1O = 1
Что и требовалось доказать.
Основное тригонометрическое тождество связывает синус угла и косинус угла. Зная одно, вы легко можете найти другое. Нужно лишь извлечь квадратный корень по формулам:
- sin α = ±
- cos α = ±
Как видите, перед корнем может стоять и минус, и плюс. Основное тригонометрическое тождество не дает понять, положительным или отрицательным был исходный синус/косинус угла.
Как правило, в задачках с подобными формулами уже есть условия, которые помогают определиться со знаком. Обычно такое условие — указание на координатную четверть. Таким образом без труда можно определить, какой знак нам требуется.
Видео:ТРИГОНОМЕТРИЧЕСКИЕ ТОЖДЕСТВА 10 класс тригонометрияСкачать

Тангенс и котангенс через синус и косинус
- Синус угла — это ордината y.
- Косинус угла — это абсцисса x.
- Тангенс угла — это отношение ординаты к абсциссе.
- Котангенс угла — это отношение абсциссы к ординате.
Из всего этого множества красивых, но не сильно понятных слов, можно сделать вывод о зависимости одного от другого. Такая связь помогает отдельно преобразовывать нужные величины.
- tg α =
- ctg α =
Исходя из определений:
- tg α =
=
- ctg α =
=
Это позволяет сделать вывод, что тригонометрические тождества

задаются sin и cos углов.
Отсюда следует, что тангенс угла — это отношение синуса угла к косинусу. А котангенс угла — это отношение косинуса к синусу.
Отдельно стоит обратить внимание на то, что тригонометрические тождества

верны для всех углов α, значения которых вписываются в диапазон.
- Например, выражение
применимо для любого угла α, не равного
+ π + z, где z — это любое целое число. В противном случае, в знаменателе будет стоять 0.
применимо для любого угла α, не равного π * z, где z — это любое целое число.
Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.
Видео:Основное тригонометрическое тождество. 9 класс.Скачать
Связь между тангенсом и котангенсом
Уж насколько очевидной кажется связь между ранее рассмотренными тождествами, настолько еще более наглядна связь между тангенсом и котангенсом одного угла.
- Тождество записывается в следующем виде:
tg α * ctg α = 1.
Такое тождество применимо и справедливо при любых углах α, значение которых не равняются π/2 * z, где z — это любое целое число. В противном случае, функции не будут определены.
Как и любое другое, данное тригонометрическое тождество подлежит доказательству. Доказывать его очень просто.
tg α * ctg α = 1.
ctg α = x/y
 и
и  ,
, получаем:

Получается, что тангенс и котангенс одного угла, при котором они имеют смысл — это взаимно обратные числа.
Если числа a и b взаимно обратные — это значит, что число a — это число, обратное числу b, а число b — это число, обратное числу a. Кроме того, это значит, что числу a обратно число b, а числу b обратно число a. Короче, и так, и эдак.
Видео:18+ Математика без Ху!ни. Формулы ПриведенияСкачать

Тангенс и косинус, котангенс и синус
Все тождества выше позволяют сделать вывод, что тангенс угла связан с косинусом угла, а котангенс угла — с синусом.
Эта связь становится очевидна, если взглянуть на тождества:
- tg 2 α + 1 =
Сумма квадрата тангенса угла и единицы равна числу, обратному квадрату косинуса этого угла.
- 1 + ctg 2 α =
Сумма единицы и квадрата котангенса угла равна числу, обратному квадрату синуса этого угла.
Вывести оба этих тождества можно из основного тригонометрического тождества:
sin 2 α + cos 2 α = 1.
- Для этого нужно поделить обе части тождества на cos 2 α, где косинус не равен нулю.
- В результате деления получаем формулу tg 2 α + 1 =
- Если обе части основного тригонометрического тождества sin 2 α + cos 2 α = 1 разделить на sin 2 α, где синус не равен нулю, то получим тождество:
1 + ctg 2 α =.
- Отсюда можно сделать вывод, что тригонометрическое тождество tg 2 α + 1 =
применимо для любого угла α, не равного
+ π + z, где z — это любое целое число.
- А тригонометрическое тождество 1 + ctg 2 α =
применимо для любого угла, не равного π * z, где z — это любое целое число.
Хорошо бы выучить все формулы и запомнить формулировки тождеств наизусть. Чтобы это сделать, сохраняйте себе табличку с основными формулами.
Основные тригонометрические тождества
sin 2 α + cos 2 α = 1
tg 2 α + 1 =
1 + ctg 2 α =
Чтобы тратить еще меньше времени на решение задач, сохраняйте таблицу значений тригонометрических функции углов, которые чаще всего встречаются в задачах.
Видео:Доказательства тригонометрических тождествСкачать

Примеры решения задач
Разберем пару задачек, для решения которых нужно знать основные тождества. Рассмотрите внимательно предложенные решения и потренируйтесь самостоятельно.
Задачка 1. Найдите cos α, tg α, ctg α при условии, что sin α = 12/13.
- Чтобы решить задачу, необходимы следующие тригонометрические тождества:
Выражаем cos α из тригонометрической единицы:
Далее подставляем значения sin α:
Вычисляем:
Нам известны значения sin α и cos α, поэтому можно легко найти тангенс, используя формулу:
Таким же образом, используя формулу, вычисляем значение котангенса:
Задачка 2. Найдите значение cos α,
если:
- Чтобы решить задачу, необходимы следующие тригонометрические тождества:
Выражаем cos α из тригонометрической единицы:
Далее подставляем значения sin α:

Подставляем значения sin α:
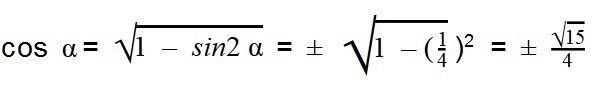
Как видите, задачи решаются достаточно просто, нужно лишь верно применять формулы основных тождеств.
Видео:Математика| Преобразование тригонометрических выражений. Формулы и задачиСкачать

Основные тригонометрические тождества: их формулировки и вывод
В статье подробно рассказывается об основных тригонометрических тождествах. Эти равенства устанавливают связь между sin , cos , t g , c t g заданного угла. При известной одной функции можно через нее найти другую.
Тригонометрические тождества для рассмотрения в денной статье. Ниже покажем пример их выведения с объяснением.
sin 2 α + cos 2 α = 1 t g α = sin α cos α , c t g α = cos α sin α t g α · c t g α = 1 t g 2 α + 1 = 1 cos 2 α , 1 + c t g 2 α = 1 sin 2 α
Видео:Формулы приведения - как их легко выучить!Скачать

Связь между sin и cos одного угла
Поговорим о важном тригонометрическом тождестве, которое считается основой основ в тригонометрии.
sin 2 α + cos 2 α = 1
Заданные равенства t g 2 α + 1 = 1 cos 2 α , 1 + c t g 2 α = 1 sin 2 α выводят из основного путем деления обеих частей на sin 2 α и cos 2 α . После чего получаем t g α = sin α cos α , c t g α = cos α sin α и t g α · c t g α = 1 — это следствие определений синуса, косинуса, тангенса и котангенса.
Равенство sin 2 α + cos 2 α = 1 является основным тригонометрическим тождеством. Для его доказательства необходимо обратиться к теме с единичной окружностью .
Пусть даны координаты точки А ( 1 , 0 ) , которая после поворота на угол α становится в точку А 1 . По определению sin и cos точка А 1 получит координаты ( cos α , sin α ) . Так как А 1 находится в пределах единичной окружности, значит, координаты должны удовлетворят условию x 2 + y 2 = 1 этой окружности. Выражение cos 2 α + sin 2 α = 1 должно быть справедливым. Для этого необходимо доказать основное тригонометрическое тождество для всех углов поворота α .
В тригонометрии выражение sin 2 α + cos 2 α = 1 применяют как теорему Пифагора в тригонометрии. Для этого рассмотрим подробное доказательство.
Используя единичную окружность, поворачиваем точку А с координатами ( 1 , 0 ) вокруг центральной точки О на угол α . После поворота точка меняет координаты и становится равной А 1 ( х , у ) . Опускаем перпендикулярную прямую А 1 Н на О х из точки А 1 .
На рисунке отлично видно, что образовался прямоугольный треугольник О А 1 Н . По модулю катеты О А 1 Н и О Н равные, запись примет такой вид: | А 1 H | = | у | , | О Н | = | х | . Гипотенуза О А 1 имеет значение равное радиусу единичной окружности, | О А 1 | = 1 . Используя данное выражение, можем записать равенство по теореме Пифагора: | А 1 Н | 2 + | О Н | 2 = | О А 1 | 2 . Это равенство запишем как | y | 2 + | x | 2 = 1 2 , что означает y 2 + x 2 = 1 .
Используя определение sin α = y и cos α = x , подставим данные угла вместо координат точек и перейдем к неравенству sin 2 α + cos 2 α = 1 .
Основная связь между sin и cos угла возможна через данное тригонометрическое тождество. Таким образом, можно считать sin угла с известным cos и наоборот. Чтобы выполнить это, необходимо разрешать sin 2 α + cos 2 = 1 относительно sin и cos , тогда получим выражения вида sin α = ± 1 — cos 2 α и cos α = ± 1 — sin 2 α соответственно. Величина угла α определяет знак перед корнем выражения. Для подробного выяснения необходимо прочитать раздел вычисление синуса, косинуса, тангенса и котангенса с использованием тригонометрических формул.
Чаще всего основную формулу применяют для преобразований или упрощений тригонометрических выражений. Имеется возможность заменять сумму квадратов синуса и косинуса на 1 . Подстановка тождества может быть как в прямом, так и обратном порядке: единицу заменяют на выражение суммы квадратов синуса и косинуса.
Видео:Тригонометрическая окружность. Как выучить?Скачать

Тангенс и котангенс через синус и косинус
Из определения косинуса и синуса, тангенса и котангенса видно, что они взаимосвязаны друг с другом, что позволяет отдельно преобразовывать необходимые величины.
t g α = sin α cos α c t g α = cos α sin α
Из определения синус является ординатой у , а косинус – абсциссой x . Тангенс – это и есть отношения ординаты и абсциссы. Таким образом имеем:
t g α = y x = sin α cos α , а выражение котангенса имеет обратное значение, то есть
c t g α = x y = cos α sin α .
Отсюда следует, что полученные тождества t g α = sin α cos α и c t g α = cos α sin α задаются с помощью sin и cos углов. Тангенс считаются отношением синуса к косинусу угла между ними, а котангенс наоборот.
Отметим, что t g α = sin α cos α и c t g α = cos α sin α верны для любого значение угла α , значения которого входят в диапазон. Из формулы t g α = sin α cos α значение угла α отлично от π 2 + π · z , а c t g α = cos α sin α принимает значение угла α , отличные от π · z , z принимает значение любого целого числа.
Видео:✓ Тригонометрия: с нуля и до ЕГЭ | #ТрушинLive #030 | Борис ТрушинСкачать

Связь между тангенсом и котангенсом
Имеется формула, которая показывает связь между углами через тангенс и котангенс. Данное тригонометрическое тождество является важным в тригонометрии и обозначается как t g α · c t g α = 1 . Оно имеет смысл при α с любым значением, кроме π 2 · z , иначе функции будут не определены.
Формула t g α · c t g α = 1 имеет свои особенности в доказательстве. Из определения мы имеем, что t g α = y x и c t g α = x y , отсюда получаем t g α · c t g α = y x · x y = 1 . Преобразовав выражение и подставив t g α = sin α cos α и c t g α = cos α sin α , получим t g α · c t g α = sin α cos α · cos α sin α = 1 .
Тогда выражение тангенса и котангенса имеет смысл того, когда в итоге получаем взаимно обратные числа.
Видео:Тригонометрические тождества. Видеоурок 22. Алгебра 10 классСкачать

Тангенс и косинус, котангенс и синус
Преобразовав основные тождества, приходим к выводу, что тангенс связан через косинус, а котангенс через синус. Это видно по формулам t g 2 α + 1 = 1 cos 2 α , 1 + c t g 2 α = 1 sin 2 α .
Определение звучит так: сумма квадрата тангенса угла и 1 приравнивается к дроби , где в числителе имеем 1 , а в знаменателе квадрат косинуса данного угла, а сумма квадрата котангенса угла наоборот. Благодаря тригонометрическому тождеству sin 2 α + cos 2 α = 1 , можно разделить соответствующие стороны на cos 2 α и получить t g 2 α + 1 = 1 cos 2 α , где значение cos 2 α не должно равняться нулю. При делении на sin 2 α получим тождество 1 + c t g 2 α = 1 sin 2 α , где значение sin 2 α не должно равняться нулю.
Из приведенных выражений получили, что тождество t g 2 α + 1 = 1 cos 2 α верно при всех значениях угла α , не принадлежащих π 2 + π · z , а 1 + c t g 2 α = 1 sin 2 α при значениях α , не принадлежащих промежутку π · z .
Видео:Почему основное тригонометрическое тождество таково?Скачать

Please wait.
Видео:ТРИГОНОМЕТРИЯ ЗА 10 МИНУТ — Arcsin, Arccos, Arctg, Arcсtg // Обратные тригонометрические функцииСкачать

We are checking your browser. mathvox.ru
Видео:Формулы приведения с нуля за 15 минут!Скачать

Why do I have to complete a CAPTCHA?
Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.
Видео:9 класс, 10 урок, Основное тригонометрическое торжество. Формула приведенияСкачать

What can I do to prevent this in the future?
If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.
If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.
Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store.
Cloudflare Ray ID: 6ce177d95c7d0004 • Your IP : 85.95.179.65 • Performance & security by Cloudflare
📽️ Видео
РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ😉 #shorts #егэ #огэ #математика #профильныйегэСкачать

[понять нельзя заучивать] Доказательство основного тригонометрического тождестваСкачать
![[понять нельзя заучивать] Доказательство основного тригонометрического тождества](https://i.ytimg.com/vi/qpaWYfOGZx8/0.jpg)
Доказательство основного тригонометрического тождестваСкачать

Доказать тригонометрическое тождество ctg²α-cos²α=ctg²αcos²α Как решить? Самый простой метод решенияСкачать

Основное тригонометрическое тождествоСкачать

Основное тригонометрическое тождество. 8 класс.Скачать





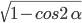
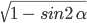
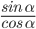
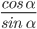
 =
= 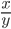 =
= 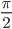 + π + z, где z — это любое целое число. В противном случае, в знаменателе будет стоять 0.
+ π + z, где z — это любое целое число. В противном случае, в знаменателе будет стоять 0.