О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
- Определение равнобедренного треугольника
- Признаки равнобедренного треугольника
- Свойства равнобедренного треугольника
- Примеры решения задач
- Равнобедренный треугольник. Онлайн калькулятор
- Определение равнобедренного треугольника
- Теорема о равнобедренном треугольнике
- Свойства равнобедренного треугольника
- Признаки равнобедренного треугольника
- 1. Признак равенства равнобедренных треугольников по основанию и боковой стороне
- 2. Признак равенства равнобедренных треугольников по боковой стороне и углу при вершине
- 3. Признак равенства равнобедренных треугольников по основанию и углу при основании
- Задачи и решения
- Доказательство треугольник равнобедренный если
- 🔍 Видео
Видео:Равнобедренный треугольник. Определение. Свойства. Теоремы и доказательства.Скачать

Определение равнобедренного треугольника
Какой треугольник называется равнобедренным?
| Равнобедренным называется треугольник, у которого две стороны равны. |
Давайте посмотрим на такой треугольник:
На рисунке хорошо видно, что боковые стороны равны. Это равенство и делает треугольник равнобедренным.
А вот как называются стороны равнобедренного треугольника:
AB и BC — боковые стороны,
AC — основание треугольника.
Для понимания материала нам придется вспомнить, что такое биссектриса, медиана и высота, если вы вдруг забыли.
Биссектриса — луч, который исходит из вершины угла и делит этот угол на два равных угла.
Даже если вы не знаете определения, то про крысу, бегающую по углам и делящую их пополам, наверняка слышали. Она не даст вам забыть, что такое биссектриса. А если вам не очень приятны крысы, то вместо нее бегать может кто угодно. Биссектриса — это киса. Биссектриса — это лИса. Никаких правил для воображения нет. Все правила — для геометрии.
Обратите внимание на рисунок. В представленном равнобедренном треугольнике биссектрисой будет отрезок BH.
Медиана — отрезок, который соединяет вершину треугольника с серединой противолежащей стороны.
Для медианы не придумали веселого правила, как с биссектрисой, но можно его придумать. Например, буддийская запоминалка: «Медиана — это Лама, бредущий из вершины треугольника к середине его основания и обратно».
В данном треугольнике медианой является отрезок BH.
Высота треугольника — перпендикуляр, опущенный из вершины треугольника на противоположную сторону или на прямую, содержащую сторону треугольника.
Высотой в представленном равнобедренном треугольнике является отрезок BH.
Видео:ПОМОГИТЕ ДОКАЗАТЬ Если две биссектрисы равны, то треугольник равнобедренныйСкачать

Признаки равнобедренного треугольника
Вот несколько нехитрых правил, по которым легко определить, что перед вами не что иное, как его величество равнобедренный треугольник.
- Если у треугольника два угла равны, то этот треугольник — равнобедренный.
- Если высота треугольника совпадает с его медианой, проведенной из того же угла, то такой треугольник — равнобедренный.
- Если высота треугольника совпадает с его биссектрисой, проведенной из того же угла, то такой треугольник — равнобедренный.
- Если биссектриса треугольника совпадает с его медианой, проведенной из того же угла, то такой треугольник снова равнобедренный!
Видео:№133. Докажите, что если биссектриса треугольника совпадает с его высотой, то треугольникСкачать

Свойства равнобедренного треугольника
Чтобы понять суть равнобедренного треугольника, нужно думать как равнобедренный треугольник, стать равнобедренным треугольником — и выучить 4 теоремы о его свойствах.
Теорема 1. В равнобедренном треугольнике углы при основании равны.
Пусть AС — основание равнобедренного треугольника. Проведем биссектрису DK. Треугольник ADK равен треугольнику CDK по двум сторонам и углу между ними (AD = DC, DK — общая, а так как DK — биссектриса, то угол ADK равен углу CDK). Из равенства треугольников следует равенство всех соответствующих элементов, значит угол A равен углу C. Изи!
Теорема 2: В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
Δ ABH = Δ CBH по двум сторонам и углу между ними (углы ABH и CBH равны, потому что BH биссектриса, AB = BC, потому что Δ ABC равнобедренный, BH — общая сторона).
Значит, во-первых, AH = HC и BH — медиана.
Во-вторых, углы BHA и BHC равны, а ещё они смежные, т. е. в сумме дают 180 градусов. Значит, они равны по 90 градусов и BH — высота.
Теорема 3: В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
Δ ABH = Δ CBH по трём сторонам (AH = CH равны, потому что BH медиана, AB = BC, потому что Δ ABC равнобедренный, BH — общая сторона).
Значит, во-первых, углы ABH и CBH равны и BH — биссектриса.
Во-вторых, углы BHA и BHC равны, а ещё они смежные, т. е. в сумме дают 180 градусов. Значит они равны по 90 градусов и BH — высота.
Теорема 4: В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.
Δ ABH = Δ CBH по признаку прямоугольных треугольников, равенство гипотенуз и соответствующих катетов (AB = BC, потому что Δ ABC равнобедренный, BH — общая сторона).
Значит, во-первых, углы ABH и CBH равны и BH — биссектриса.
Во-вторых, AH = HC и BH — медиана.
Видео:№110. Докажите, что если медиана треугольника совпадает с его высотой, то треугольникСкачать

Примеры решения задач
Нет ничего приятнее, чем поупражняться и поискать углы и стороны в равнобедренном треугольнике. Ну… почти ничего.
Задачка раз. Дан ΔABC с основанием AC: ∠C = 80°, AB = BC. Найдите ∠B.
Поскольку вы уже знакомы с различными теоремами, то для вас не секрет, что углы при основании в равнобедренном треугольнике равны, а треугольник ABC — равнобедренный, так как AB = BC.
Значит, ∠A = ∠C = 80°.
Не должно вас удивить и то, что сумма углов треугольника равна 180°.
∠B = 180° − 80° − 80° = 20°.
Задачка два. В треугольнике ABC провели высоту BH, угол CAB равен 50°, угол HBC равен 40°. Найдите сторону BC, если BA = 5 см.
Сумма углов треугольника равна 180°, а значит в Δ ABH мы можем узнать угол ABH, который будет равен 180° − 50° − 90° = 40°.
А ведь получается, что углы ABH и HBC оба равны по 40° и BH — биссектриса.
Ну и раз уж BH является и биссектрисой, и высотой, то Δ ABC — равнобедренный, а значит BC = BA = 5 см.
Изучать свойства и признаки равнобедренного треугольника лучше всего на курсах по математике с опытными преподавателями в Skysmart.
Видео:Геометрия Докажите, что если в треугольнике две высоты равны, то он равнобедренный.Скачать

Равнобедренный треугольник. Онлайн калькулятор
С помощю этого онлайн калькулятора можно найти неизвестные элементы (стороны, углы) а также периметр, площадь, высоты равнобедренного треугольника. Теоретическую часть и численные примеры смотрите ниже.
| Открыть онлайн калькулятор |
Видео:7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать

Определение равнобедренного треугольника
Определение 1 (Евклид). Треугольник, в котором длины двух сторон равны между собой называется равнобедренным треугольником.
Равные стороны равнобедренного трекугольника называются боковыми сторонами. Третья сторона равнобедренного треугольника называется основанием треугольника (Рис.1).
Угол между боковыми сторонами равнобедненного треугольника (( small angle A ) ) называется вершинным углом. Углы между основанием и боковыми сторонами (( small angle B, angle C ) ) называются углами при основании.
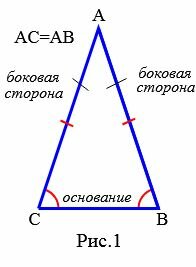 |
Существует более общее определение равнобедненого треугольника:
Определение 2 (Современная трактовка). Треугольник, в котором длины хотя бы двух сторон равны между собой называется равнобедренным треугольником.
Из определения 2 следует, что равносторонний треугольник является частным случаем равнобедренного треугольника. Действительно, в качестве равных сторон можно взять любые две стороны равностороннего треугольника, а третья сторона будет основанием.
Видео:Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать

Теорема о равнобедренном треугольнике
Теорема 1. Углы, прилежащие к основанию равнобедренного треугольника равны.
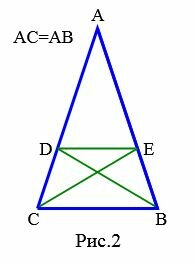 |
Доказательство (доказательство Прокла). Пусть задан равнобедренный треугольник ABC, где AB=AC (Рис.2). Докажем, что ( small angle B= angle C. ) Возьмем любую точку D на стороне AC и точку E на стороне AB так, чтобы AD=AE. Проведем отрезки DE, CE, BD. Треугольники ABD и ACE равны по двум сторонам и углу между ними: AE=AD, AC=AB, угол ( small angle A ) общий (см. статью на странице Треугольники. Признаки равенства треугольников). Отсюда следует:
| ( small CE=BD,) | (1) |
| ( small angle ACE=angle ABD.) | (2) |
Из ( small AB=AC) и ( small AD=AE ) следует:
| ( small CD=BE.) | (3) |
Рассмотрим треугольники CBE и BCD. Они равны по трем сторонам: ( small CE=BD,) ( small CD=BE ,) сторона ( small BC ) общая. Отсюда следует, что
| ( small angle ECB= angle DBC. ) | (4) |
Из (2) и (4) следует, что ( small angle B= angle C. )
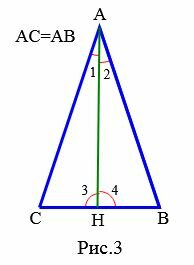 |
Доказательство (Вариант 2). Пусть задан равнобедренный треугольник ABC, где AB=AC (Рис.3). Проведем биссектрису ( small AH ) треугольника. Тогда ( small angle CAH=angle BAH. ) Докажем, что ( small angle B= angle C. ) Треугольники AHB и AHC равны по двум сторонам и углу между ними: AC=AB, сторона ( small AH ) общая, ( small angle CAH=angle BAH. ) Отсюда следует: ( small angle B= angle C. )
Видео:Геометрия 7 класс (Урок№13 - Равнобедренный треугольник.)Скачать

Свойства равнобедренного треугольника
Теорема 2. В равнобедренном треугольнике биссектриса проведенная к основанию является медианой и высотой.
Доказательство. Рассмотрим равнобедренный треугольник ABC, где AB=AC, а AH− биссектриса треугольника (Рис.3). Треугольники AHB и AHC равны по двум сторонам и углу между ними: AC=AB, сторона ( small AH ) общая, ( small angle 1=angle 2. ) Тогда ( small CH=HB, ) ( small angle 3=angle 4. ) Равенство ( small CH=HB ) означает, что ( small AH ) является также медианой треугольника ABC. Углы ( small angle 3) и ( angle 4 ) смежные. Следовательно их сумма равна 180° и, поскольку эти углы равны, то каждый из этих углов равен 90°. Тогда ( small AH ) является также высотой треугольника ( small ABC. ) Поскольку высота ( small AH ) перпендикулярна к ( small BC ) и ( small CH=HB, ) то ( small AH ) является также серединным перпендикуляром к основанию равнобедренного треугольника.
Мы доказали, что биссектриса, медиана, высота и серединный перпендикуляр равнобедренного треугольника, проведенные к основанию совпадают.
Исходя из теоремы 2 можно сформулировать следующие теоремы, доказательство которых аналогично доказательству теоремы 2:
Теорема 3. В равнобедренном треугольнике медиана проведенная к основанию является биссектрисой и высотой.
Теорема 4. В равнобедренном треугольнике высота проведенная к основанию является биссектрисой и медианой.
Видео:№159. Докажите, что два равнобедренных треугольника равны, если боковая сторона и угол, противолежащСкачать

Признаки равнобедренного треугольника
Признак 1. Если в треугольнике две стороны равны, то треугольник является равнобедренным.
Признак 1 следует из определения 1.
Признак 2. Если в треугольнике два угла равны, то треугольник является равнобедренным.
Доказательство признака 2 смотрите в статье Соотношения между сторонами и углами треугольника (Следствие 2. Признак равнобедренного треугольника).
Признак 3. Если в треугольнике высота проведенная к одной стороне совпадает с медианой проведенной к этой же стороне, то треугольник является равнобедренным.
Доказательство. Пусть в треугольнике ( small ABC ) ( small AH ) является высотой и медианой (Рис.4). Тогда ( small angle 3=angle4=90°, ) ( small CH=HB. ) Треугольники ( small AHC ) и ( small AHB ) равны по двум сторонам и углу между ними (первый признак равенства треугольников): ( small AH ) − общая сторона, ( small CH=HB, ) ( small angle 3=angle4. ) Следовательно ( small AB=AC. )
Признак 4. Если в треугольнике высота проведенная к одной стороне совпадает с биссектрисой проведенной к этой же стороне, то треугольник является равнобедренным.
Доказательство. Пусть в треугольнике ( small ABC ) ( small AH ) является высотой и биссектрисой (Рис.4). Тогда ( small angle 3=angle4=90°, ) ( small angle 1=angle2. ) Треугольники ( small AHC ) и ( small AHB ) равны по стороне и прилежащим двум углам (второй признак равенства треугольников): ( small AH ) − общая сторона, ( small angle 1=angle 2, ) ( small angle 3=angle4. ) Следовательно ( small AB=AC. )
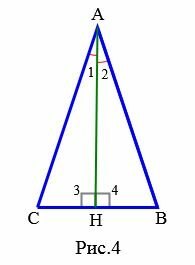 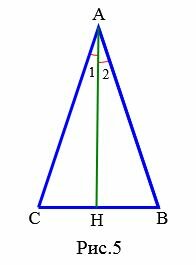 |
Признак 5. Если в треугольнике биссектриса проведенная к одной стороне совпадает с медианой проведенной к этой же стороне, то треугольник является равнобедренным.
Доказательство (Вариант 1). Пусть в треугольнике ( small ABC ) ( small AH ) является биссектрисой и медианой (Рис.5). Тогда
| ( small angle 1=angle2, ) ( small CH=HB. ) | (5) |
Применим теорему синусов для треугольника ( small AHC ):
| ( small frac = frac . ) | (6) |
Применим теорему синусов для треугольника ( small AHB ):
| ( small frac = frac . ) | (7) |
тогда, из (5), (6), (7) получим:
| ( small frac = frac . ) | (8) |
Следовательно ( small sin angle C= sin angle B. ) Поскольку сумма всех углов треугольника равна 180°, то нам интересует синус углов от 0 до 180°. Учитывая это получим, что синусы углов равны в двух случаях: 1) ( small angle C= angle B, ) 2) ( small angle C= 180° — angle B. ) Поскольку сумма двух углов треугольника меньше 180°: ( small angle C + angle B Доказательство (Вариант 2). Пусть в треугольнике ( small ABC ) ( small AH ) является биссектрисой и медианой, т.е. ( small angle 1=angle 2, ) ( small CH=HB ) (Рис.6). На луче ( small AH ) отложим отрезок ( small HD ) так, чтобы ( small AH=HD. ) Соединим точки ( small C ) и ( small D. )
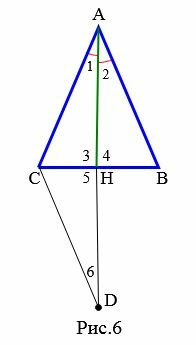 |
Треугольники ( small AHB ) и ( small DHC ) равны по двум сторонам и углу между ними (первый признак равенства треугольников). Действительно: ( small AH=HD, ) ( small CH=HB, ) ( small angle 4=angle 5 ) (углы 4 и 5 вертикальные). Тогда ( small AB=CD, ) ( small angle 6=angle 2. ) Отсюда ( small angle 6=angle 1. ) Получили, что треугольник ( small CAD ) равнобедренный (признак 2). Тогда ( small AC=CD. ) Но ( small AB=CD ) и, следовательно ( small AB=AC. ) Получили, что треугольник ( small ABC ) равнобедренный.
Видео:ОГЭ Задание 25 Доказать что треугольник равнобедренныйСкачать

1. Признак равенства равнобедренных треугольников по основанию и боковой стороне
Если основание и боковая сторона одного равнобедренного треугольника соответственно равны основанию и боковой стороне другого равнобедненного треугольника, то эти треугольники равны.
Действительно. Поскольку треугольник равнобедренный, то боковые стороны равны. То есть три стороны одного равнобедренного треугольника соответственно равны трем сторонам другого равнобедненного треугольника. А по третьему признаку равенства треугольников, эти треугольники равны.
Видео:№232. Верно ли утверждение: если треугольник равнобедренный, то один из его внешнихСкачать

2. Признак равенства равнобедренных треугольников по боковой стороне и углу при вершине
Если боковая сторона и угол при вершине одного равнобедренного треугольники соответственно равны боковой стороне и углу при вершине другого равнобедренного треугольника, то такие треугольники равны.
Действительно. Так как боковые стороны равнобедненного треугольника равны, то имеем: две стороны и угол между ними одного треугольника соотвественно равны двум сторонам и углу между ними другого треугольника. Тогда по первому признаку равенства треугольников, эти реугольники равны.
Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

3. Признак равенства равнобедренных треугольников по основанию и углу при основании
Если основание и угол при основании равнобедренного треугольника соответственно равны основанию и углу при основании другого равнобедренного треугольника, то такие треугольники равны.
Доказательство. В равнобедренном треугольнике углы при основании равны. тогда имеем: основание и две углы одного равнобедненного треугольника равны основанию и двум углам другого равнобедненного треугольника. Тогда эти треугольники равны по второму признаку равенства треугольников.
Видео:Равнобедренный треугольник. 7 класс.Скачать

Задачи и решения
Задача 1. Известны основание ( small a=5 ) и высота ( small h=6 ) равнобедренного треугольника. Найти углы, боковые стороны, периметр, площадь.
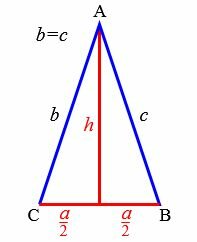 |
Решение. Найдем боковые стороны ( small b ) и ( small c ) равнобедренного треугольника. Воспользуемся теоремой Пифагора:
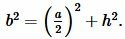 |
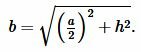 | (9) |
Подставляя значения ( small a ) и ( small h ) в (9), получим:
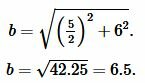 |
Боковая сторона ( small c ) равнобедренного треугольника равна:
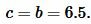 |
Найдем периметр треугольника. Периметр треугольника равен сумме длин его сторон:
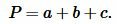 | (10) |
Подставляя значения ( small a=5, ) ( small b=6.5 ) и ( small c=6.5 ) в (10), получим:
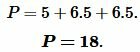 |
Найдем угол ( small B ) равнобедренного треугольника:
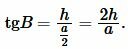 | (11) |
Подставляя значения ( small a=5, ) ( small h=6 ) в (11), получим:
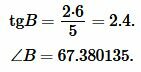 |
Тогда угол ( small C ) равнобедренного треугольника равен:
 |
Поскольку сумма всех углов треугольника равна 180°, то имеем:
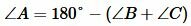 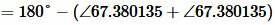 , , |
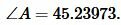 |
Площадь треугольника можно вычислить из формулы:
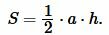 | (12) |
Подставляя значения ( small a=5, ) ( small h=6 ) в (12), получим:
Видео:№134. Докажите, что равнобедренные треугольники равны, если основание и прилежащий кСкачать

Доказательство треугольник равнобедренный если
Из этой теоремы следует, что в треугольнике против равных углов лежат равные стороны .
Если медиана треугольника является его биссектрисой, то этот треугольник равнобедренный.
Рассмотрим треугольник ABC , у которого отрезок BM — медиана и биссектриса. Надо доказать, что AB = BC .
На луче BM отложим отрезок MD , равный отрезку BM (рис. 171).
В треугольниках AMD и CMB имеем: AM = MC (так как по условию BM — медиана), BM = MD по построению, углы AMD и CMB равны как вертикальные. Следовательно, треугольники AMD и CMB равны по первому признаку равенства треугольников.
Тогда стороны AD и BC , углы ADM и CBM равны как соответственные элементы равных треугольников.
Так как BD — биссектриса угла ABC , то ∠ ABM = ∠ CBM . Поскольку ∠ CBM = ∠ ADM , то получаем, что ∠ ABM = ∠ ADM .
Тогда по теореме 10.3 получаем, что треугольник DAB — равнобедренный, откуда AD = AB . И уже доказано, что AD = BC . Следовательно, AB = BC .
Задача. В треугольнике ABC проведена биссектриса BM (рис. 172), ∠ BAK = 70°, ∠ AKC = 110°. Докажите, что BM ⊥ AK .
Решение. Так как углы BKA и AKC — смежные, то ∠ BKA = 180° — ∠ AKC . Тогда ∠ BKA = 180° — 110° = 70°.
Следовательно, в треугольнике ABK получаем, что ∠ BAK = ∠ BKA = 70°. Треугольник ABK — равнобедренный с основанием AK , и его биссектриса BO ( O — точка пересечения AK и BM ) является также высотой, т. е. BM ⊥ AK .
- Сформулируйте признаки равнобедренного треугольника.
- Какова связь между равными углами и равными сторонами треугольника?
232. В треугольнике ABC медиана BK перпендикулярна стороне AC . Найдите ∠ ABC , если ∠ ABK = 25°.
233. Серединный перпендикуляр стороны AC треугольника ABC проходит через вершину B . Найдите ∠ C , если ∠ A = 17°.
234. В треугольнике ABC известно, что ∠ ACB = 90°, ∠ A = ∠ B = 45°, CK — высота. Найдите сторону AB , если CK = 7 см.
235. На рисунке 173 ∠ AMK = ∠ ACB , AK = MK . Докажите, что ∆ ABC — равнобедренный.
236. Прямая, перпендикулярная биссектрисе угла A , пересекает его стороны в точках B и C . Докажите, что ∆ ABC — равнобедренный.
237. Биссектрисы AM и CK углов при основании AC равнобедренного треугольника ABC пересекаются в точке O . Докажите, что ∆ AOC — равнобедренный.
238. В треугольнике ABC биссектриса BK является его высотой. Найдите периметр треугольника ABC , если периметр треугольника ABK равен 16 см и BK = 5 см.
239. Верно ли утверждение:
1) если медиана и высота треугольника, проведённые из одной вершины, не совпадают, то этот треугольник не является равнобедренным;
2) если биссектриса треугольника делит противолежащую сторону пополам, то этот треугольник равнобедренный?
240. Медианы AE и CF , проведённые к боковым сторонам BC и AB равнобедренного треугольника ABC , пересекаются в точке M . Докажите, что треугольник AMC — равнобедренный.
241. Точки M и K принадлежат соответственно боковым сторонам AB и BC равнобедренного треугольника ABC , AM = CK . Отрезки AK и CM пересекаются в точке O . Докажите, что ∆ AOC — равнобедренный.
242. На сторонах AB и BC треугольника ABC отметили соответственно точки D и E так, что ∠ EAC = ∠ DCA . Отрезки AE и CD пересекаются в точке F , DF = EF . Докажите, что ∆ ABC — равнобедренный.
243. Через середину D стороны AB треугольника ABC проведены прямые, перпендикулярные биссектрисам углов ABC и BAC . Эти прямые пересекают стороны AC и BC в точках M и K соответственно. Докажите, что AM = BK .
244. Медиана AM треугольника ABC перпендикулярна его биссектрисе BK . Найдите сторону AB , если BC = 16 см.
245. Прямая, проходящая через вершину A треугольника ABC перпендикулярно его медиане BD , делит эту медиану пополам. Найдите отношение длин сторон AB и AC треугольника ABC .
246. В треугольнике ABC известно, что ∠ C = 90°, ∠ A = 67,5°, ∠ B = 22,5°, CK — биссектриса треугольника ABC , CM — биссектриса треугольника BCK (рис. 174). Докажите, что точка M — середина отрезка AB .
247. Длины сторон треугольника, выраженные в сантиметрах, равны трём идущим подряд натуральным числам. Найдите стороны этого треугольника, если одна из его медиан перпендикулярна одной из его биссектрис.
248. В треугольнике ABC известно, что AB = 3 см, BC = 4 см, AC = 6 см. На стороне BC отметили точку M такую, что CM = 1 см. Прямая, проходящая через точку M перпендикулярно биссектрисе угла ACB , пересекает отрезок AC в точке K , а прямая, проходящая через точку K перпендикулярно биссектрисе угла BAC , пересекает прямую AB в точке D . Найдите длину отрезка BD .
Упражнения для повторения
249. На прямой последовательно отметили точки A , B , C , D , E и F так, что AB = BC = CD = DE = EF . Найдите отношения AB : CF , AB : BF , BD : AE .
250. Найдите углы, образованные при пересечении двух прямых, если один из них на 42° больше половины второго угла.
Наблюдайте, рисуйте, конструируйте, фантазируйте
251. Разрежьте прямоугольник размером 4 × 9 на две равные части, из которых можно сложить квадрат.
🔍 Видео
Как распознать равнобедренный треугольник? #shortsСкачать

Признаки равенства треугольников. 7 класс.Скачать

Геометрия. 7 класс. Теоремы. Т5. Первое свойство равнобедренного треугольника.Скачать

Свойства равнобедренного треугольника. 7 класс.Скачать

Геометрия Докажите, что если медиана треугольника совпадает с его биссектрисой, то этот треугольникСкачать

Задание 25 Доказать что треугольник равнобедренныйСкачать

























