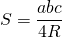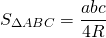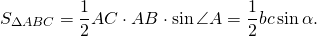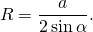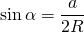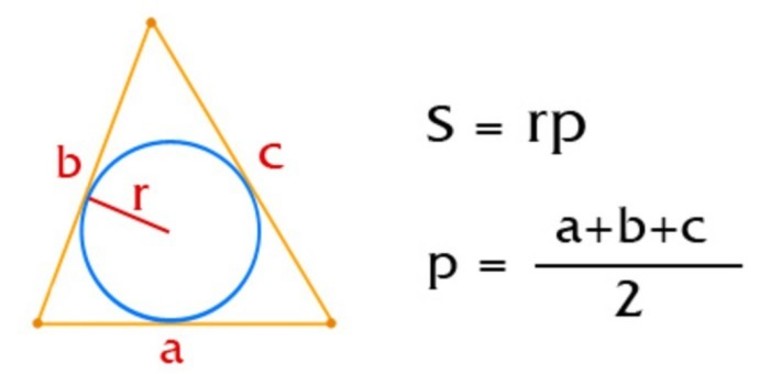Доказательство теоремы площади треугольника через радиус описанной окружности (4 видео)

Площадь треугольника через радиус описанной окружности

Как найти площадь треугольника через радиус описанной окружности?

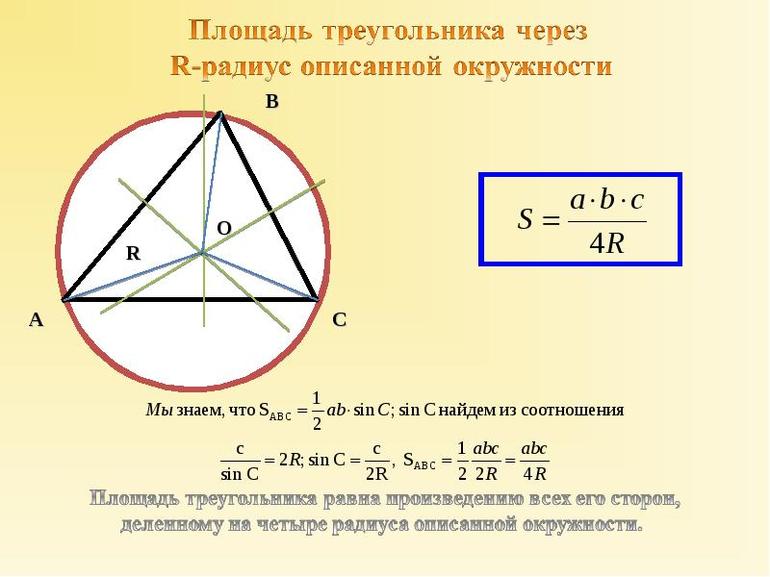
Площадь треугольника равна частному от деления произведения сторон треугольника на четыре радиуса описанной около треугольника окружности.

Формула для нахождения площади треугольника через радиус описанной окружности:

окружность (O; R) — описанная,

Выразим из этой формулы синус альфа

и подставим полученное выражение в первую формулу

Содержание

Площадь треугольника через радиус описанной окружности — формулы и примеры определения
Фигура с тремя сторонами
Вписанный в окружность треугольник
Пересечение медиатрис
Типы фигур и точка O
Формулы для определения площади
Решение задач
Please wait.
We are checking your browser. mathvox.ru
Why do I have to complete a CAPTCHA?
What can I do to prevent this in the future?
📺 Видео

Видео:Геометрия 9 класс (Урок№14 - Теорема о площади треугольника.)Скачать

Площадь треугольника через радиус описанной окружности — формулы и примеры определения

Видео:9 класс, 12 урок, Теорема о площади треугольникаСкачать

Фигура с тремя сторонами

Чтобы понять, как рассчитывать площадь треугольника, вписанного в окружность, необходимо иметь четкое представление о рассматриваемой фигуре. Каждый школьник знает о геометрическом объекте, который ограничен тремя отрезками. Основными элементами треугольника являются следующие:

Стороны, которых у фигуры три. Они могут быть равны по длине или отличаться друг от друга. При этом всегда справедливым остается тот факт, что длина любой стороны меньше суммы длин двух других.
Вершины — это три точки, которые образованы на пересечении соответствующих сторон. Каждая из них характеризуется определенным значением угла. Для трех углов треугольника справедливо следующее равенство: ∠A + ∠B + ∠C = 180 °, где латинскими буквами названы соответствующие вершины.

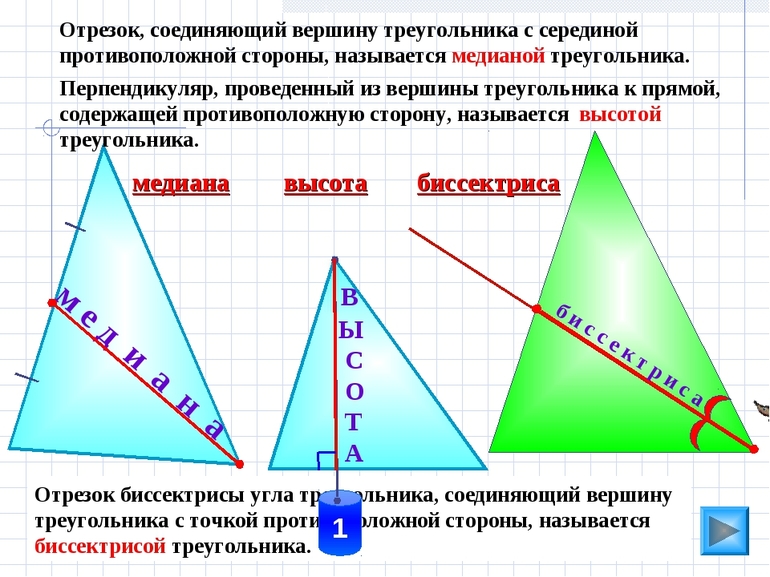
Помимо вершин и сторон, треугольник характеризуется дополнительными отрезками, которые часто используются для доказательства теорем и решения геометрических задач. К имеющим специальное название отрезкам относятся такие:

Медиана — делящий треугольник на две фигуры с одинаковой площадью отрезок. Он проходит через вершину и середину противоположной стороны. Все три медианы пересекаются в одной точке, которая является массовым центром рассматриваемого геометрического объекта.
Биссектриса — отрезок, который делит пополам угол при вершине. Все три биссектрисы, как и медианы, пересекаются в одной точке, которая является центром вписанной в треугольник окружности.
Высота — перпендикуляр, который через вершину опускается на противоположную сторону. Высоты часто используются при вычислении площадей.
Средняя линия — проходящая через середины двух сторон линия, которая является параллельной третьей. Обе стороны отсекают отрезок, длина которого составляет половину от длины противоположной стороны.
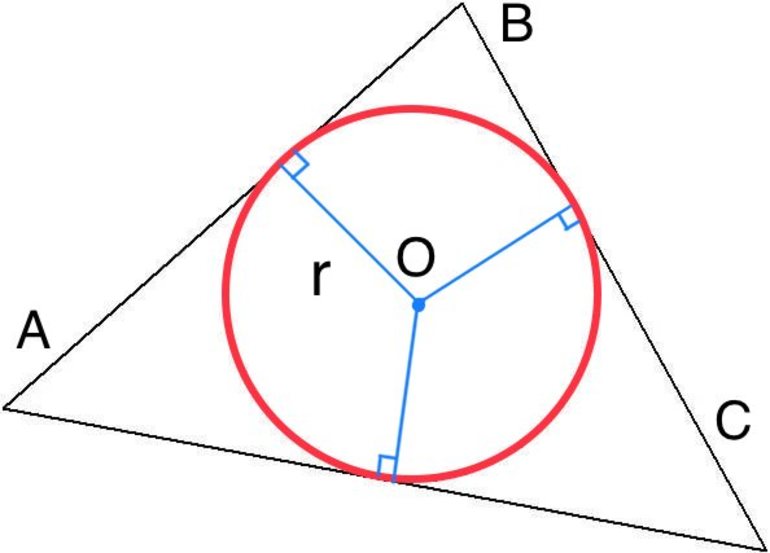
Медиатриса или серединный перпендикуляр — это прямая линия, которая пересекает под углом 90 ° сторону треугольника. Важным свойством медиатрис является тот факт, что точка из пересечения — это центр описанной вокруг фигуры окружности.

Видео:Геометрия Доказательство Площадь треугольника равна произведению его полупериметра и радиусаСкачать

Вписанный в окружность треугольник

Чтобы уметь вычислять площадь описанного треугольника, следует понимать, о каком взаимном расположении многоугольника и окружности идет речь. Согласно определению, если через все вершины полигона проходит окружность, значит, он считается вписанным в нее. Это простое определение не всегда выполняется для произвольного многоугольника, однако, для любой правильной фигуры оно будет справедливым, например, для квадрата или прямоугольника.

Касательно треугольника следует отметить, что он является единственным многоугольником, для которого всегда можно найти центр и радиус описывающей его окружности. Причем независимо от того, какой тип фигуры рассматривается.

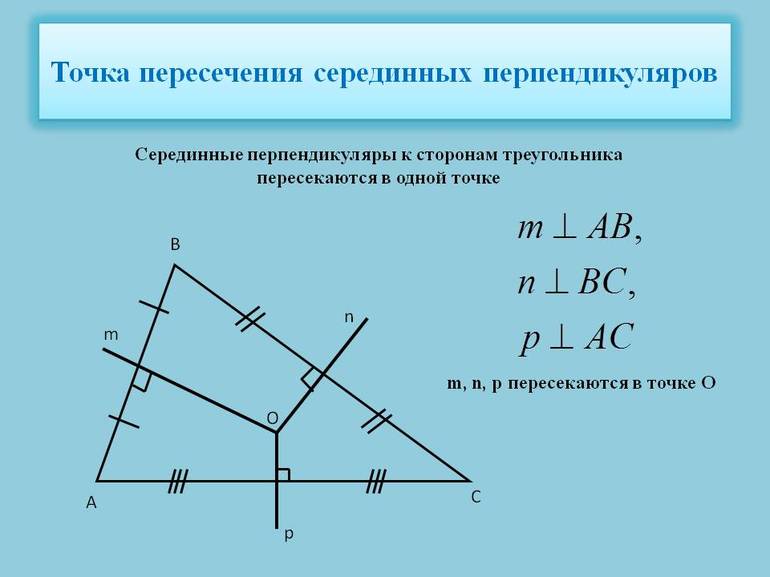
Пересечение медиатрис

В рассматриваемой фигуре имеется три разных медиатрисы. Каждую из них построить несложно для любой из сторон. Для построения следует выполнить последовательность действий:

Выбрать сторону.
Установить циркуль в один из концов стороны и провести дугу окружности, которая будет пересекать сторону дальше, чем посередине.
Пункт 2 выполнить, установив циркуль во второй конец стороны.
Соединить точки пересечения дуг в одну линию. Она является медиатрисой.

Из проделанных построений следует один важный факт для всех треугольников: точка пересечения их медиатрис является центром описывающей фигуру окружности. Доказать это утверждение легко. Например, имеется треугольник ABC. Пусть проведена медиатриса m к стороне AB. Любая из точек, принадлежащих прямой m, находится на одинаковом расстоянии от вершин A и B.

Пусть проведена еще одна медиатриса n к стороне BC. Прямые m и n пересекаются в точке O. Поскольку O принадлежит обеим медиатрисам, то она, с одной стороны, находится на одном расстоянии от A и B, с другой стороны, она находится на одинаковой дистанции от вершин B и C. Этот факт дает право сделать вывод о том, что расстояния OA, OB и OC равны. Если их обозначить буквой R, то можно говорить, что R — радиус окружности с центром в точке O, которая проходит через три вершины треугольника, то есть описывается его.

Очевидно, что третья медиатриса также пройдет через O. В противном случае будут существовать три разные точки, которые одновременно будут находиться на одинаковом расстоянии от трех вершин треугольника и будут лежать в одной плоскости с ним, а это невозможно из свойств двумерного пространства.

Типы фигур и точка O

Поскольку для треугольника любого типа можно провести описывающую его окружность, то представляет интерес рассмотреть вопрос положения ее центра O. В общем случае существуют три типа рассматриваемого многоугольника:

С острыми углами, то есть все они менее 90 °. К этим треугольникам относятся равносторонние. Для них центр описанной окружности всегда расположен внутри фигуры.
С одним тупым углом и двумя острыми. Это может быть либо равнобедренный треугольник, либо фигура общего типа. Для нее точка O всегда расположена вне области, ограниченной сторонами многоугольника, то есть за его пределами.
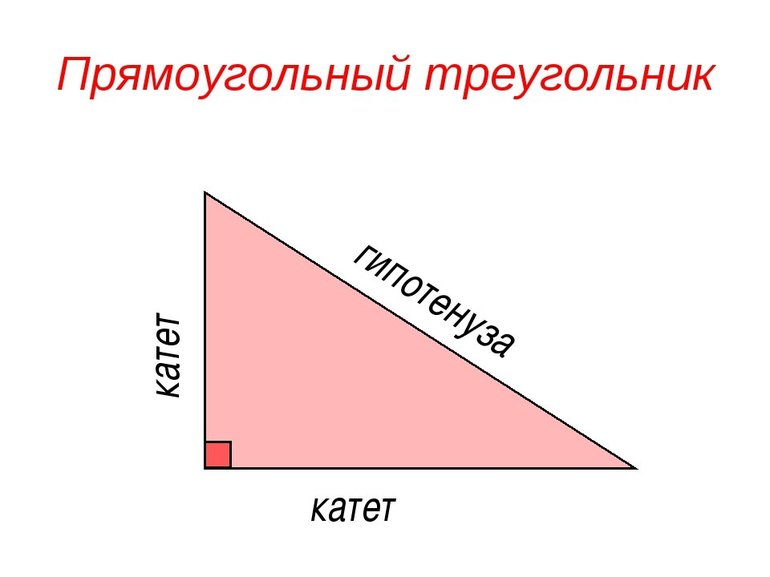
Прямоугольный. Для такого типа треугольников центр описанной окружности расположен точно посередине гипотенузы. Это свойство треугольника, которое доказывается просто, если рассмотреть точку пересечения двух средних линий, проведенных относительно катетов. Поскольку O лежит посередине гипотенузы, то последняя является диаметром описанной окружности. Любой треугольник, который опирается на диаметр одной из своих сторон, и третья вершина которого лежит на окружности, является прямоугольным.

Очевидно, что если треугольник является полностью вырожденным, то провести описывающую его окружность нельзя, поскольку такая фигура обращается в прямой отрезок.

Формулы для определения площади

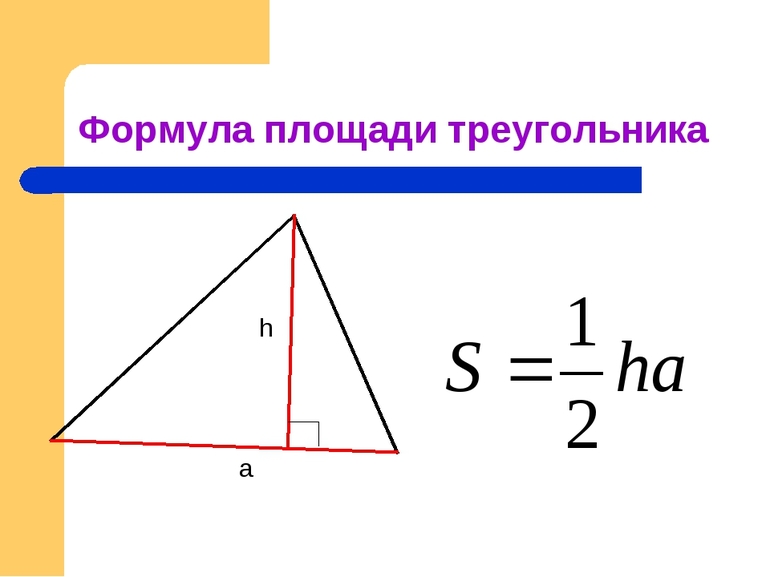
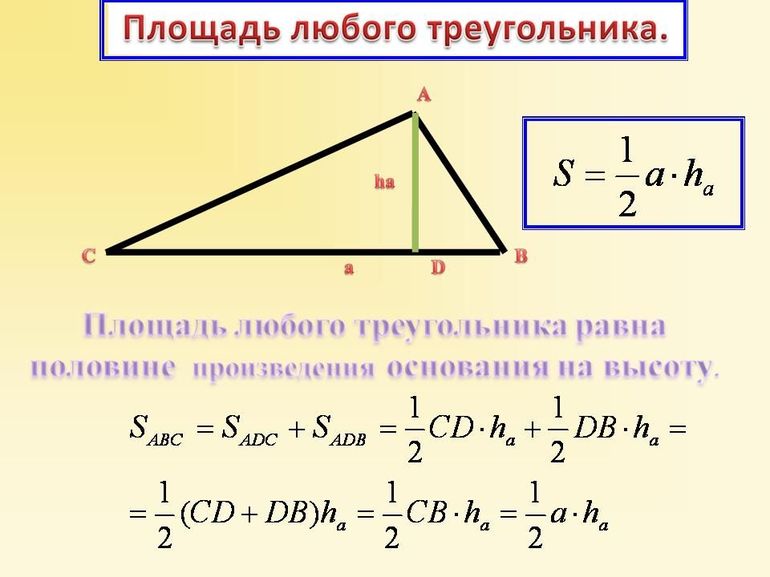
Как известно, площадь треугольника произвольного типа может быть рассчитана, как половина произведения высоты h на длину основания a: S = ½*h*a. Существует также еще одно универсальное выражение для определения S — это половина модуля векторного произведения направляющих отрезков, образующих любые две стороны.

Что касается формул площади треугольника, описанного около окружности, то нужно отметить, что известны несколько из них. Соответствующие равенства имеют следующий вид:

Где a, b, c — длины соответствующих сторон треугольника, ha, hb, hc — высоты, проведенные к a, b и c, соответственно. Видно, что все три формулы требуют знание минимум 4 параметров для рассматриваемой фигуры (радиус и три высоты или три длины сторон).

Полезно также привести формулу для расчета радиуса R:

Здесь p = (a+b+c)/2 — полупериметр треугольника. Следует отметить, что знаменатель в выражении для радиуса является не чем иным, как формулой Герона для расчета площади S фигуры.

Видео:Теорема синусов и косинусов. Связь площади треугольника с радиусами вписанной и описанной окружностиСкачать

Решение задач

Как правило, прямое использование формул площади треугольника через окружность описанную является невозможным для типичных геометрических задач. Для их решения необходимо внимательно проанализировать условие и использовать все имеющиеся знания для определения неизвестных в выражениях для S через R.

Для некоторых задач может потребоваться использование уравнений прямых, которые на плоскости в векторной форме имеют вид:

(x, y) = (x0, y0) + α*(v1, v2).

Здесь (x, y) и (x0, y0) — координаты произвольной и известной точек прямой, соответственно, (v1, v2) — координаты направляющего вектора, α — числовой параметр.

Для закрепления полученных знаний полезно решить одну простую задачу. Известно, что один из острых углов в прямоугольном треугольнике составляет 30 °. Чему равна площадь этой фигуры, если радиус описанной окружности для нее составляет 12 см.

Для решения задачи воспользуемся следующим выражением через радиус окружности, описанной около треугольника, для площади:

Пусть c — это гипотенуза, тогда c = 2*R = 24 см. Катеты a и b можно связать с гипотенузой функциями синуса и косинуса:

a = c*cos (α) = 24*3 0,5 /2 = 20,7846 см;
b = c*sin (α) = 24*½ = 12 см.

Подставляя полученные значения в формулу для S через R, можно получить ответ:

S = a*b*c/(4*R) = 20,7846*12*24/(4*12) ≈ 124,71 см 2 .

Важно понимать, что формулы расчета площади рассматриваемого многоугольника через радиус описанной окружности используются редко, поскольку они могут быть заменены аналогичными более простыми выражениями, как в случае с высотой и основанием. В решенной задаче, например, можно было не применять указанную для S формулу, а просто рассчитать полупроизведение катетов:

S = ½*a*b = ½*20,7846*12 ≈ 124,71 см 2 .

Таким образом, вокруг каждого треугольника можно описать окружность радиуса R, центр которой расположен в точке пересечения его серединных перпендикуляров (медиатрис). Существует несколько формул для вычисления площади фигуры через радиус R, однако, все они требуют знания либо сторон, либо высот треугольника, и в большинстве случаев могут быть заменены более простыми выражениями при решении задач.

Видео:✓ Новая формула площади треугольника | Ботай со мной #108 | Борис ТрушинСкачать

Please wait.

Видео:Геометрия Доказательство Площадь S треугольника можно вычислить по формуле S = abc/(4R) где a b cСкачать

We are checking your browser. mathvox.ru

Видео:100. Теорема о площади треугольникаСкачать

Why do I have to complete a CAPTCHA?

Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.

Видео:Площадь треугольника через радиус описанной окружности: ОГЭ - ЕГЭСкачать

What can I do to prevent this in the future?

If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.

If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.

Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store.

Cloudflare Ray ID: 6d4fb3b82d5f163a • Your IP : 85.95.179.65 • Performance & security by Cloudflare