Доказательство теоремы пифагора треугольников

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Видео:Простое доказательство теоремы Пифагора. Понятнее, чем в учебникеСкачать

Основные понятия

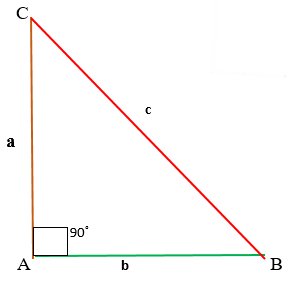
Теорема Пифагора, определение: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.

Гипотенуза — сторона, лежащая напротив прямого угла.

Катет — одна из двух сторон, образующих прямой угол.

Формула Теоремы Пифагора выглядит так:

где a, b — катеты, с — гипотенуза.

Из этой формулы можно вывести следующее:

• a = √c 2 − b 2
• b = √c 2 − a 2
• c = √a 2 + b 2

Для треугольника со сторонами a, b и c, где c — большая сторона, действуют следующие правила:

• если c 2 2 + b 2 , значит угол, противолежащий стороне c, является острым.
• если c 2 = a 2 + b 2 , значит угол, противолежащий стороне c, является прямым.
• если c 2 > a 2 +b 2 , значит угол, противолежащий стороне c, является тупым.

Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Теорема Пифагора: доказательство

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Дано: ∆ABC, в котором ∠C = 90º.

Доказать: a 2 + b 2 = c 2 .

Пошаговое доказательство:

• Проведём высоту из вершины C на гипотенузу AB, основание обозначим буквой H.
• Прямоугольная фигура ∆ACH подобна ∆ABC по двум углам:

• Также прямоугольная фигура ∆CBH подобна ∆ABC:

• Введем новые обозначения: BC = a, AC = b, AB = c.

• Из подобия треугольников получим: a : c = HB : a, b : c = AH : b.

• Значит a 2 = c * HB, b 2 = c * AH.
• Сложим полученные равенства:

a 2 + b 2 = c * HB + c * AH

a 2 + b 2 = c * (HB + AH)

a 2 + b 2 = c * AB

Видео:Самое простое Доказательство теоремы ПифагораСкачать

Обратная теорема Пифагора: доказательство

Если сумма квадратов двух сторон треугольника равна квадрату третьей стороны, то такой треугольник является прямоугольным.

Дано: ∆ABC

Доказать: ∠C = 90º

Пошаговое доказательство:

• Построим прямой угол с вершиной в точке C₁.
• Отложим на его сторонах отрезки C₁A₁ = CA и C₁B₁ = CB.

• Проведём отрезок A₁B₁.
• Получилась фигура ∆A₁B₁C₁, в которой ∠C₁=90º.

• В этой фигуре ∆A₁B₁C₁ применим теорему Пифагора: A₁B₁ 2 = A₁C₁ 2 + B₁C₁ 2 .
• Таким образом получится:

• Значит, в фигурах треугольниках ∆ABC и ∆A₁B₁C₁:

1. C₁A₁ = CA и C₁B₁ = CB по результату построения,
2. A₁B₁ = AB по доказанному результату.

• Поэтому, ∆A₁B₁C₁ = ∆ABC по трем сторонам.
• Из равенства фигур следует равенство их углов: ∠C =∠C₁ = 90º.

Обратная теорема доказана.

Видео:Edu: Сколькими способами можно доказать теорему Пифагора?Скачать

Решение задач

Задание 1. Дан прямоугольный треугольник ABC. Его катеты равны 6 см и 8 см. Какое значение у гипотенузы?

Как решаем:

Пусть катеты a = 6 и b = 8.

По теореме Пифагора c 2 = a 2 + b 2 .

Подставим значения a и b в формулу:
c 2 = 6 2 + 8 2 = 36 + 64 = 100
c = √100 = 10.

Задание 2. Является ли треугольник со сторонами 8 см, 9 см и 11 см прямоугольным?

• Выберем наибольшую сторону и проверим, выполняется ли теорема Пифагора:

Ответ: треугольник не является прямоугольным.

Видео:Теорема Пифагора. 8 КЛАСС | Математика | TutorOnlineСкачать

Различные способы доказательства теоремы Пифагора

учащаяся 9 «А» класса

Теорема Пифагора по праву считается самой важной в курсе геометрии и заслуживает при­стального внимания. Она являет­ся основой решения множества геометрических задач, базой для изучения теоретического и практического курса геометрии в дальнейшем. Теорема окружена богатей­шим историческим материалом, связанным с её появлением и способами доказательства. Изучение истории развития геометрии прививает любовь к данному предмету, способствует развитию познава­тельного интереса, общей культу­ры и творчества, а так же развивает навыки научно-исследовательской работы.

В результате поисковой деятельности была достигнута цель работы, заключающаяся в пополнении и обобщении знаний по доказательству теоремы Пифагора. Удалось найти и рассмотреть различные способы доказательства и углубить знания по теме, выйдя за страницы школьного учебника.

Собранный материал ещё больше убеждает в том, что теорема Пифагора является великой теоремой геометрии, имеет огромное теоретическое и практическое значение.

Введение. Историческая справка 5 Основная часть 8

3. Заключение 19

4. Используемая литература 20
1. ВВЕДЕНИЕ. ИСТОРИЧЕСКАЯ СПРАВКА.

Суть истины вся в том, что нам она — навечно,

Когда хоть раз в прозрении ее увидим свет,

И теорема Пифагора через столько лет

Для нас, как для него, бесспорна, безупречна.

На радостях богам был Пифагором дан обет:

За то, что мудрости коснулся бесконечной,

Он сто быков заклал, благодаря предвечных;

Моленья и хвалы вознес он жертве вслед.

С тех пор быки, когда учуят, тужась,

Что к новой истине людей опять подводит след,

Ревут остервенело, так что слушать мочи нет,

Такой в них Пифагор вселил навеки ужас.

Быкам, бессильным новой правде противостоять,

Что остается? — Лишь глаза закрыв, реветь, дрожать.

Неизвестно, каким способом доказывал Пифагор свою теорему. Несомненно лишь то, что он открыл ее под силь­ным влиянием египетской науки. Частный случай теоре­мы Пифагора — свойства треугольника со сторонами 3, 4 и 5 — был известен строителям пирамид задолго до рожде­ния Пифагора, сам же он более 20 лет обучался у египет­ских жрецов. Сохранилась легенда, которая гласит, что, доказав свою знаменитую теорему, Пифагор принес богам в жертву быка, а по другим источникам, даже 100 быков. Это, однако, противоречит сведениям о моральных и ре­лигиозных воззрениях Пифагора. В литературных источ­никах можно прочитать, что он «запрещал даже убивать животных, а тем более ими кормиться, ибо животные имеют душу, как и мы». Пифагор питался только медом, хлебом, овощами и изредка рыбой. В связи со всем этим более правдоподобной можно считать следующую запись: «. и даже когда он открыл, что в прямоугольном треугольнике гипо­тенуза имеет соответствие с катетами, он принес в жертву быка, сделанного из пшеничного теста».

Популярность теоремы Пифагора столь велика, что ее доказательства встречаются даже в художественной литературе, например, в рассказе известного английско­го писателя Хаксли «Юный Архимед». Такое же Доказа­тельство, но для частного случая равнобедренного пря­моугольного треугольника приводится в диалоге Плато­на «Менон».

«Далеко-далеко, куда не летают даже самолеты, находится страна Геометрия. В этой необычной стране был один удиви­тельный город — город Теорем. Однажды в этот город пришла красивая девочка по имени Гипотенуза. Она попробовала снять комнату, но куда бы она ни обращалась, ей всюду отказывали. Наконец она подошла к покосившемуся домику и постучала. Ей открыл мужчина, назвавший себя Прямым Углом, и он предло­жил Гипотенузе поселиться у него. Гипотенуза осталась в доме, в котором жили Прямой Угол и два его маленьких сына по имени Катеты. С тех пор жизнь в доме Прямого Угла пошла по-ново­му. На окошке гипотенуза посадила цветы, а в палисаднике развела красные розы. Дом принял форму прямоугольного тре­угольника. Обоим катетам Гипотенуза очень понравилась и они попросили ее остаться навсегда в их доме. Ло вечерам эта друж­ная семья собирается за семейным столом. Иногда Прямой Угол играет со своими детишками в прятки. Чаще всего искать при­ходится ему, а Гипотенуза прячется так искусно, что найти ее бывает очень трудно. Однажды во время игры Прямой Угол подметил интересное свойство: если ему удается найти катеты, то отыскать Гипотенузу не составляет труда. Так Прямой Угол пользуется этой закономерностью, надо сказать, очень успешно. На свойстве этого прямоугольного треугольника и основана тео­рема Пифагора.»

(Из книги А. Окунева «Спасибо за урок, дети»).

Шутливая формулировка теоремы:

Если дан нам треугольник

И притом с прямым углом,

То квадрат гипотенузы

Мы всегда легко найдем:

Катеты в квадрат возводим,

Сумму степеней находим –

И таким простым путем

К результату мы придем.

Изучая алгебру и начала анализа и геометрию в 10 классе, я убедилась в том, что кроме рассмотренного в 8 классе способа доказательства теоремы Пифагора существуют и другие способы доказательства. Представляю их на ваше обозрение.
2. ОСНОВНАЯ ЧАСТЬ.

Теорема. В прямоугольном треугольнике квадрат

гипотенузы равен сумме квадратов катетов.

Пользуясь свойствами площадей многоугольников, установим замечательное соотношение между гипотенузой и катетами прямоугольного треугольника.

Рассмотрим прямоугольный треугольник с катетами а, в и гипотенузой с (рис.1, а).

Докажем, что с²=а²+в².

Доказательство.

Достроим треугольник до квадрата со стороной а + в так, как показано на рис. 1, б. Площадь S этого квадрата равна (а + в)² . С другой стороны, этот квадрат составлен из четырех равных прямоугольных треугольников, площадь каждого из которых равна ½ав , и квадрата со стороной с, поэтому S= 4 * ½ав + с² =2ав + с².

Теорема доказана.
2 СПОСОБ.

После изучения темы «Подобные треугольники» я выяснила, что можно применить подобие треугольников к доказательству теоремы Пифагора. А именно, я воспользовалась утверждением о том, что катет прямоугольного треугольника есть среднее пропорциональное для гипотенузы и отрезка гипотенузы, заключённого между катетом и высотой, проведённой из вершины прямого угла.

Рассмотрим прямоугольный треугольник с прямым углом С, СD– высота (рис. 2). Докажем, что АС² +СВ² = АВ².

На основании утверждения о катете прямоугольного треугольника:

АС = , СВ = .

Возведем в квадрат и сложим полученные равенства:

АС² = АВ * АD, СВ² = АВ * DВ;

АС² + СВ² = АВ * ( АD + DВ), где АD+DB=AB, тогда

Доказательство закончено.
3 СПОСОБ.

К доказательству теоремы Пифагора можно применить определение косинуса острого угла прямоугольного треугольника. Рассмотрим рис. 3.

Пусть АВС – данный прямоугольный треугольник с прямым углом С. Проведем высоту СD из вершины прямого угла С.

По определению косинуса угла:

cos А = АD/АС = АС/АВ. Отсюда АВ * АD = АС²

cos В = ВD/ВС = ВС/АВ.

Отсюда АВ * ВD = ВС² .

Складывая полученные равенства почленно и замечая, что АD + DВ = АВ, получим:

Доказательство закончено.
4 СПОСОБ.

Изучив тему «Соотношения между сторонами и углами прямоугольного треугольника», я думаю, что теорему Пифагора можно доказать ещё одним способом.

Рассмотрим прямоугольный треугольник с катетами а, в и гипотенузой с. (рис. 4).

sinВ= в/с ; cosВ= a/с, то, возведя в квадрат полученные равенства, получим:

Сложив их, получим:

1= (в²+ а²) / с², следовательно,

Данное доказательство основано на разрезании квадратов, построенных на катетах (рис. 5), и укладывании полученных частей на квадрате, по­строенном на гипотенузе.

Для доказательства на катете ВС строим BCD ABC (рис.6 ). Мы знаем, что пло­щади подобных фигур отно­сятся как квадраты их сход­ственных линейных размеров:

Вычитая из первого равенства второе, получим

,

,

с2 = а2 + b2.

ABС, = 90°, ВС = а, АС=b, АВ = с.

Пусть катет b а. Продолжим отре­зок СВ за точку В и построим треугольник BMD так, что­бы точки М и А лежали по одну сторону от прямой CD и, кроме того, BD = b, BDM = 90°, DM = a, тогда BMD = ABC по двум сторонам и углу между ними. Точки А и М соединим отрезками AM. Имеем MD CD и AC CD, значит, прямая АС параллельна прямой MD. Так как MD

Видео:Доказательство теоремы Пифагора. Геометрия 8 классСкачать

Теорема Пифагора

Теорема Пифагора – в прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы. Вы узнаете, как доказать теорему, формула Пифагора и как решать задачи.

Видео:Теорема ПифагораСкачать

История теоремы

Однако название получено в честь учёного только по той причине, что он первый и, даже единственный человек, который смог доказать теорему.

Немецкий историк математики Кантор утверждал, что о теореме было известно ещё египтянами приблизительно в 2300 году до н. э. Он считал, раньше строили прямые углы благодаря прямоугольным треугольникам со сторонами 3, 4 и 5.

Известный учёный Кеплер говорил, что у геометрии есть незаменимое сокровище – это теорема Пифагора, благодаря которой можно вывести большинство теорем в геометрии.

Раньше теорему Пифагора называли “теоремой невесты” или “теоремой нимфы”. А всё дело в том, что её чертёж был очень похож на бабочку или нимфу. Арабы же, когда переводили текст теоремы, решили, что нимфа означает невеста. Так и появилось интересное название у теоремы.

Нужна помощь в написании работы?

Написание учебной работы за 1 день от 100 рублей. Посмотрите отзывы наших клиентов и узнайте стоимость вашей работы.

Видео:Как быстро и легко выучить теорему по математике. На примере теоремы ПифагораСкачать

Теорема Пифагора, формула

Теорема Пифагора – в прямоугольном треугольнике сумма квадратов катетов () равна квадрату гипотенузы (). Это одна из основополагающих теорем эвклидовой геометрии.

Формула:

Как уже говорилось, есть много разнообразных доказательств теоремы с разносторонними математическими подходами. Однако, более часто используют теоремы, связанные с площадями.

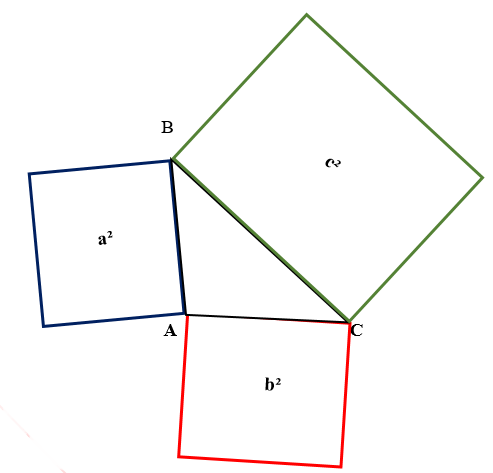
Построим на треугольнике квадраты ( синий , зеленый , красный )

То есть сумма площадей квадратов, построенных на катетах равняется площади квадрата, построенном на гипотенузе. Соответственно, площади этих квадратов равны – . Это и есть геометрическое объяснение Пифагора.

Видео:Шаталов за одну минуту доказывает теорему, на которую традиционно выделяется 45 минут урока!Скачать

Доказательство теоремы методом площадей: 1 способ

Докажем, что .

Рассмотрим всё тот же треугольник с катетами a, b и гипотенузой c.

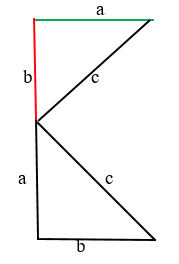
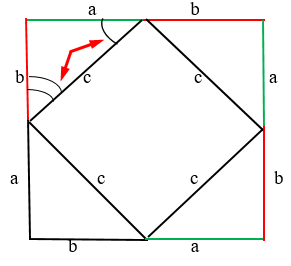
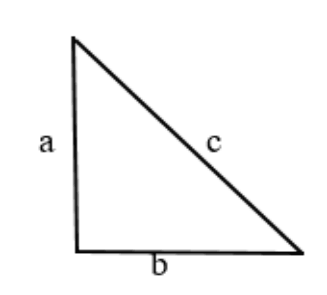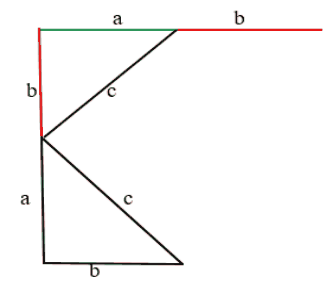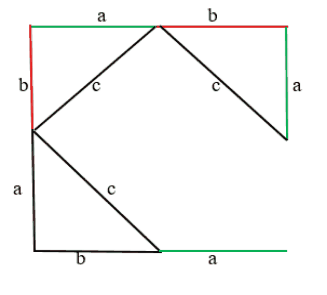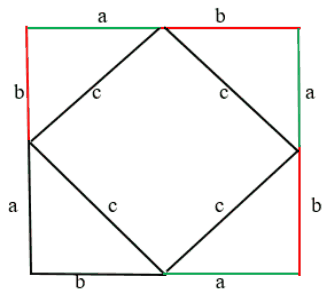
1. Достраиваем прямоугольный треугольник до квадрата. От катета “а” продолжаем линию вверх на расстояние катета “b” (красная линия).
2. Далее ведём линию нового катета “а” вправо (зелёная линия).
3. Два катета соединяем гипотенузой “с”.

Получается такой же треугольник, только перевёрнутый.

Аналогично строим и с другой стороны: от катета “а” проводим линию катета “b” и вниз “а” и “b” А снизу от катета “b” проводим линию катета “а”. В центре от каждого катета провели гипотенузы “с”. Таким образом гипотенузы образовали квадрат в центре.

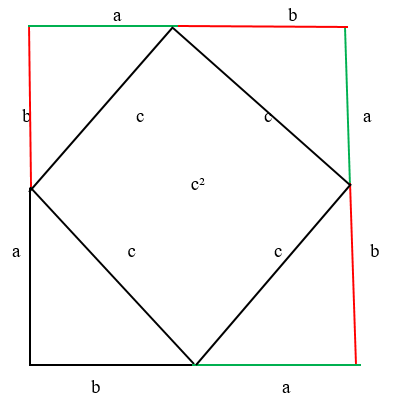
Этот квадрат состоит из 4-х одинаковых треугольников. А площадь каждого прямоугольного треугольника = половина произведения его катетов. Соответственно, . А площадь квадрата в центре = , так как все 4 гипотенузы со стороной . Стороны четырёхугольника равны, а углы прямые. Как нам доказать, что углы прямые? Очень просто. Возьмём всё тот же квадрат:

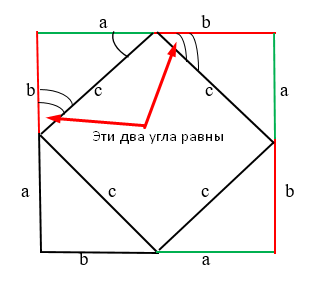
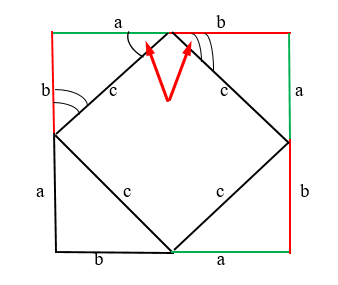
Мы знаем, что эти два угла, показаны на рисунке, являются 90 градусам. Так как треугольники равны, значит следующий угол катета “b” равен предыдущему катету “b”:

Сумма этих двух углов = 90 градусов. Соответственно, предыдущий угол тоже 90 градусов. Конечно же, аналогично и с другой стороны. Соответственно, у нас действительно квадрат с прямыми углами.

Так как острые углы прямоугольного треугольника в общей сложности равняются 90 градусам, то угол четырёхугольника так же будет равен 90 градусов, ведь 3 угла в сумме = 180 градусов.

Соответственно, площадь квадрата складывается из четырёх площадей одинаковых прямоугольных треугольников и площади квадрата, который образован гипотенузами.

Таким образом, получили квадрат со стороной . Мы знаем, что площадь квадрата со стороной – это будет квадрат его стороны. То есть . Этот квадрат состоит из четырёх одинаковых треугольников.

1. Запишем: .
2. Далее смотрим, что площадь прямоугольного треугольника – это половина произведения его катетов. Поэтому дальше записываем:т
3. Также надо прибавить площадь квадрата, который находится в центре между треугольниками со стороной “с”. И теперь получим:

1. Раскрываем скобки и получаем:
2. Сокращаем . Получается:

И это значит, что мы доказали теорему Пифагора.

ВАЖНО. Если находим гипотенузу, тогда складываем два катета, а затем ответ выводим из корня. При нахождении одного из катетов: из квадрата длины второго катета вычитаем квадрат длины гипотенузы и находим квадратный корень.

Видео:8 класс, 16 урок, Теорема ПифагораСкачать

Примеры решения задач

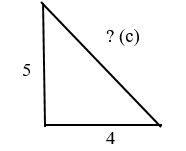
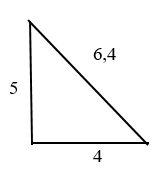
Дано: прямоугольный треугольник с катетами 4 и 5.

Найдите гипотенузу. Пока её обозначим “с”

Сумма квадратов катетов равняется квадрату гипотенузы. В нашем случае – .

Воспользуемся теоремой Пифагора:

Итак, , а . Катеты в сумме получают 41.

Тогда . То есть квадрат гипотенузы равен 41.

Квадрат числа 41 = 6,4.

Мы нашли гипотенузу.

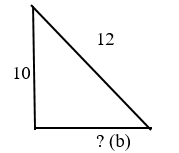
Дано: прямоугольный треугольник, где гипотенуза = 12, один катет = 10

Найдите второй катет.

Обозначим неизвестный катет – b.

Воспользуемся теоремой Пифагора:

, а

Находим

Если , тогда просто

Второй катет (b) равен 6,6.

Видео:Теорема Пифагора. 8 класс.Скачать

Заключение

Итак, мы рассмотрели теорему Пифагора, смогли привести ее доказательство и привели несколько примеров задач и их решений.

Запомните раз и навсегда: квадраты гипотенузы равен суммы квадратов катетов: (это вся теорема Пифагора).

📺 Видео

Теорема Пифагора (доказательство) - геометрия 8 классСкачать

Наглядное доказательство теоремы ПифагораСкачать

Теорема ПифагораСкачать

ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

теорема Пифагора с доказательствомСкачать

Теорема, которую скрывали 200 летСкачать

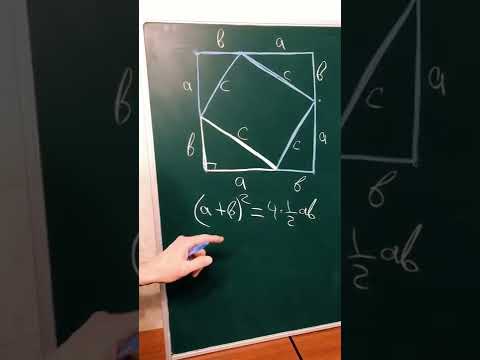
Доказательство теоремы Пифагора. Способ 2. Через подобные треугольникиСкачать

ТЕОРЕМА ПИФАГОРА 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

Доказательство теоремы ПифагораСкачать