Сделаем дополнительные построения:
Продолжим AD до точки K, так, что DK = AD. Продолжим A1D1 до точки K1, так, что D1K1 = A1D1. В ΔADC и ΔDBK: AD = DK
∠ADC = ∠BDK (как вертикальные) BD = DC (т.к. AD — медиана)
Таким образом, ΔADC = ΔDBK по 1-му признаку, и ∠DAC = ∠DKB АС = BK.

задача №7
к главе «§ 3. Признаки равенства треугольников».
Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Признаки равенства треугольников с использованием медианы, биссектрисы и высоты
Признаки равенства треугольников с использованием медианы, биссектрисы и высоты. Решетников Михаил Сергеевич, Харютченко Данил Александрович. Муниципальный этап.
Видео:Признаки равенства треугольников. 7 класс.Скачать

Скачать:
| Вложение | Размер |
|---|---|
| Признаки равенства треугольников с использованием медианы, биссектрисы и высоты | 1.67 МБ |
Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Предварительный просмотр:
МУНИЦИПАЛЬНЫЙ ЭТАП XI ВСЕРОССИЙСКОГО ДЕТСКОГО КОНКУРСА
НАУЧНО-ИССЛЕДОВАТЕЛЬСКИХ И ТВОРЧЕСКИХ РАБОТ
«ПЕРВЫЕ ШАГИ В НАУКЕ»
Секция: информационные технологии; математика;
Тема: Признаки равенства треугольников с использованием медианы, биссектрисы и высоты
Авторы: Решетников Михаил Сергеевич, МОУ «Октябрьская СОШ им. Ю. Чумака», 8 класс
Харютченко Данил Александрович, МОУ «Октябрьская СОШ им. Ю. Чумака», 8 класс
Научный руководитель: Шевченко Елена Михайловна, учитель математики МОУ «Октябрьская СОШ им. Ю. Чумака»
Место выполнения работы: Белгородская область, Белгородский район, поселок Октябрьский
Признаки равенства треугольников с использованием медианы, биссектрисы и высоты
Треугольник – одна из самых простых и загадочных геометрических фигур. Вот уже два с половиной тысячелетия открываются его новые и новые свойства. Со времен «Начал» Евклида геометрия строится на основе трех признаков равенства треугольников. Исходя из того, что в треугольнике выделяют шесть основных элементов: три внутренних угла и три соответственно противолежащие им стороны, равенство треугольников устанавливается по равенству трех из шести элементов. Три следующих признака являются фундаментом геометрии:
- по двум сторонам и углу между ними;
- по стороне и прилежащим к ней углам;
- по трём сторонам.
Эти признаки отличаются простотой формулировки и часто применяются при решении задач базового уровня. Рассматривая более сложные задачи, приходится фактически «изобретать велосипед», дважды или трижды применять известные признаки, конструируя из них решение. Это приводит к следующему выводу: известных трех признаков не всегда достаточно.
Если учесть, что для каждого треугольника однозначно определяются три медианы, три биссектрисы и три высоты, то число элементов треугольника увеличивается до 15. В связи с этим возникает следующая гипотеза: наряду с основными тремя признаками равенства треугольников можно сформулировать и доказать новые признаки равенства треугольников с использованием медианы, биссектрисы и высоты, знание которых поможет в решении многих геометрических задач.
Объектом данного исследования является треугольник и его элементы, в том числе медианы, биссектрисы и высоты; предмет исследования – признаки равенства треугольников.
- сформулировать и доказать новые признаки равенства треугольников;
- обосновать эффективность применения новых признаков равенства треугольников при решении геометрических задач.
- проанализировать определения и свойства медианы, биссектрисы и высоты;
- выявить зависимость между равенством отдельных элементов и равенством треугольников;
- определить типы геометрических задач, при решении которых целесообразно применение полученных признаков.
В работе применялись методы научного исследования: анализ, сравнение, математическое моделирование.
Для доказательства новых признаков равенства треугольников использовались только первый, второй и третий признаки равенства треугольников, что обеспечивает простоту доказательства и доступность данной работы для широкого круга школьников.
Видео:Геометрия 7 класс (Урок№15 - Решение задач на признаки равенства треугольников.)Скачать

Медиана треугольника
Определение . Медианой треугольника называют отрезок, соединяющий вершину треугольника с серединой противоположной стороны (рис 1).
Поскольку в каждом треугольнике имеется три вершины, то в каждом треугольнике можно провести три медианы.
На рисунке 1 медианой является отрезок BD .
Утверждение 1 . Медиана треугольника делит его на два треугольника равной площади ( равновеликих треугольника).
Доказательство . Проведем из вершины B треугольника ABC медиану BD и высоту BE (рис. 2),
и заметим, что (см. раздел нашего справочника «Площадь треугольника»)
Поскольку отрезок BD является медианой, то
что и требовалось доказать.
Утверждение 2 . Точка пересечения двух любых медиан треугольника делит каждую из этих медиан в отношении 2 : 1 , считая от вершины треугольника.
Доказательство . Рассмотрим две любых медианы треугольника, например, медианы AD и CE , и обозначим точку их пересечения буквой O (рис. 3).
Обозначим середины отрезков AO и CO буквами F и G соответственно (рис. 4).
Теперь рассмотрим четырёхугольник FEDG (рис. 5).
Сторона ED этого четырёхугольника является средней линией в треугольнике ABC . Следовательно,
Сторона FG четырёхугольника FEDG является средней линией в треугольнике AOC . Следовательно,
Отсюда вытекает, что точка O делит каждую из медиан AD и CE в отношении 2 : 1 , считая от вершины треугольника.
Следствие . Все три медианы треугольника пересекаются в одной точке.
Доказательство . Рассмотрим медиану AD треугольника ABC и точку O , которая делит эту медиану в отношении 2 : 1 , считая от вершины A (рис.7).
Поскольку точка, делящая отрезок в заданном отношении, является единственной, то и другие медианы треугольника будут проходить через эту точку, что и требовалось доказать.
Определение . Точку пересечения медиан треугольника называют центроидом треугольника.
Утверждение 3 . Медианы треугольника делят треугольник на 6 равновеликих треугольников (рис. 8).
Доказательство . Докажем, что площадь каждого из шести треугольников, на которые медианы разбивают треугольник ABC , равна 
💡 Видео
Геометрия 7 класс (Урок№10 - Первый признак равенства треугольников.)Скачать

Первый признак равенства треугольников. 7 класс.Скачать

7 класс, 15 урок, Первый признак равенства треугольниковСкачать

Признаки равенства треугольников. Практическая часть. 7 класс.Скачать

Геометрия 7 класс (Урок№14 - Второй и третий признаки равенства треугольников.)Скачать

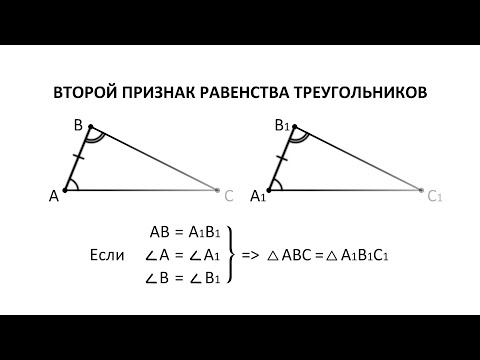
Геометрия. 7 класс. Теоремы. Т7. Второй признак равенства треугольников.Скачать
Геометрия 7 класс (Урок№12 - Медианы треугольника. Биссектрисы треугольника. Высоты треугольника.)Скачать

8. Медиана треугольника и её свойства.Скачать

7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

Доказательство 3 его признака равенства треугольниковСкачать

Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать

Второй признак равенства треугольников. 7 класс.Скачать

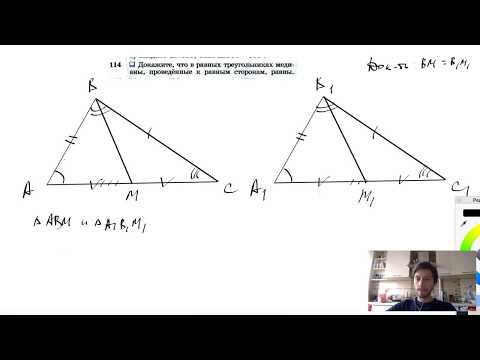
№114. Докажите, что в равных треугольниках медианы, проведенные к равным сторонам, равны.Скачать
7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать

7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать

Первый признак равенства треугольников | Теорема + доказательствоСкачать















