Доказательство что фигура треугольник (7 видео)

Признаки треугольников

Признаки треугольника — это признаки, с помощью
которых можно доказать, что геометрическая фигура
является треугольником.

При решении задач, так или иначе связанных с треугольником,
бывает нужно определить, что за фигуру нужно решить в задаче.
Для определения типа и вида геометрической фигуры нужно знать
признаки. В этой статье рассмотрено три признака треугольника, пять
признаков равнобедренного треугольника, четыре признака
равностороннего треугольника, и три признака прямоугольного треугольника.
Зная эти признаки можно с легкостью определить является ли
геометрическая фигура треугольником.

Содержание

III признака треугольника
Love Soft
Инструменты пользователя
Инструменты сайта
Боковая панель
Навигация
Связь
Содержание
Треугольник
Определение
Материал 7 класса
Внешний угол треугольника
Признаки равенства треугольников
Дополнительные признаки
Треугольник — жесткая фигура
Средняя линия треугольника
Биссектриса
Инцентр
Медиана
Теорема ван Ламуна
Теорема Аполлония
Центроид или центр масс
Основные факты о треугольниках
Готовьтесь к экзамену вместе с образовательным порталом «Школково»
🔥 Видео

Видео:Геометрия 7 класс (Урок№9 - Треугольник.)Скачать

III признака треугольника

Геометрическая фигура является треугольником, если состоит из трёх точек,
не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки.
Геометрическая фигура является треугольником, если у нее три стороны и три угла.
Геометрическая фигура является треугольником, если сумма всех углов 180°.

Кроме просто треугольника есть еще виды треугольников. Существует три
основных вида треугольников: равнобедренный, равносторонний, прямоугольный.
Кроме признаков треугольника мы рассмотрим еще и признаки видов треугольника.

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Love Soft

Инструменты пользователя

Инструменты сайта

Боковая панель

Содержание

Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Треугольник

Треугольник является первой фигурой, которую нельзя разложить на более простые фигуры… и поэтому считается фундаментом любой вещи, имеющей границы и форму.

Видео:Сила формы треугольника. Жёсткая фигура и прочная конструкция. Физика. ГеометрияСкачать

Определение

I. Треугольником называется геометрическая фигура, состоящая из трех отрезков, соединяющих три точки, не лежащие на одной прямой.

Сумма трех сторон треугольника называется его периметром.

Каждый треугольник разделяет плоскость на две части: внутреннюю и внешнюю области. Фигуру, состоящую из сторон треугольника и его внутренней области, также называют треугольником.

II. Треугольник — это многоугольник, у которого имеется ровно три угла (и три вершины).

III. Треугольник — замкнутая ломаная из трех отрезков.

Видео:Первый признак равенства треугольников. 7 класс.Скачать

Материал 7 класса

В равнобедренном треугольнике углы при основании равны, а биссектриса, проведенная к основанию, является медианой и высотой.

Если в треугольнике два угла равны, то он равнобедренный.

Катет прямоугольного треугольника, лежащий против угла 30 градусов, равен половине гипотенузы (модель).

Из любой точки окружности ее диаметр, не выходящий из этой точки, виден под прямым углом.

Внешний угол треугольника

Внешний угол треугольника — угол, образованный стороной треугольника и продолжением его другой стороны.

При каждой вершине треугольника имеются два внешних угла.

Внешний угол треугольника равен сумме двух углов, не смежных с ним.

Откуда в математике могли появиться внешние углы. Когда европейцы увидели пирамиды древнего Египта, они были потрясены увиденным. Им захотелось измерить эти грандиозные сооружения. Вот только внутренний угол пирамиды измерить не представляется возможным. Можно измерить внешний угол и высчитать внутренний.

Внутренняя область треугольника ABC — общая часть внутренних областей трех углов А, В и С этого треугольника.

Признаки равенства треугольников

Дополнительные признаки

Треугольник — жесткая фигура

Жесткая фигура — это фигура, не подверженная деформации.

Соединив дощечки с помощью гвоздей в четырехугольник, можно изменять градусную меру углов четырехугольника, не меняя длины его сторон.

Можно менять величины углов у пятиугольников, шестиугольников и многоугольников с большим количеством сторон.

С треугольником так поступить не удастся. Стороны треугольника определяют его углы однозначно. Треугольник не подвержен деформации. Поэтому треугольник — жесткая фигура. Из всех многоугольников только треугольник является жесткой фигурой.

Это свойство треугольника используется, в частности, при создании железных ажурных конструкций. Мосты, башни, подъемные краны, каркасы зданий, опоры для высоковольтных линий электропередач изготавливают таким образом, чтобы они содержали как можно больше треугольных элементов.

Средняя линия треугольника

Средняя линия треугольника — отрезок, соединяющий середины двух сторон этого треугольника.

Средняя линия треугольника параллельна третьей стороне и равна её половине. (модель)

При проведении всех трёх средних линий образуются 4 равных треугольника, подобных исходному с коэффициентом 1/2. Центральный из этих 4 одинаковых треугольников называется дополнительным треугольником. Медианы и центр тяжести данного треугольника ABC совпадают с медианами и центром тяжести дополнительного треугольника A’B’C’.

Средняя линия отсекает треугольник, который подобен данному, а его площадь равна одной четверти площади исходного треугольника.

См. также

Видео:Признаки равенства треугольников. 7 класс.Скачать

Биссектриса

Биссектриса треугольника — отрезок биссектрисы угла.

В треугольнике большей стороне соответствует меньшая биссектриса.

Угол между биссектрисами двух углов зависит только от третьего угла (легко вывести формулу: половина третьего угла + прямой угол)

Биссектриса угла треугольника делит противоположную сторону пропорционально прилежащим сторонам.

Инцентр

Инцентр — точка пересечения биссектрис треугольника.

Теорема. Три биссектрисы треугольника (любого!) пересекаются в одной точке – и эта точка – центр вписанной окружности.

Инцентр делит биссектрису угла A в отношении $frac$, где a, b, c — стороны треугольника. доказательство Используйте то свойство, что биссектриса треугольника делит противоположную сторону на части, пропорциональные прилежащим сторонам. Примените его сначала для всего треугольника, а затем для двух треугольников, на которые он разделяется биссектрисой.

Формула Эйлера. Расстояние между инцентром I и центром описанной окружности O выражается: $OI^2=R^2-2Rr$, где R и r — радиусы описанной и вписанной окружностей соответственно.

Биссектрисы делят треугольник на 6 треугольников. Центры вписанных окружностей этих треугольников принадлежат эллипсу. (статья)

Видео:7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать

Медиана

Определение: Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.

У каждого треугольника есть три медианы.

Большей стороне треугольника соответствует меньшая медиана.

В прямоугольном треугольнике медиана, проведённая из вершины с прямым углом, равняется половине гипотенузы.

Каждая медиана делит треугольник на 2 равновеликих треугольника (одинаковой площади).

Три медианы делят треугольник на 6 равновеликих треугольников.

Теорема ван Ламуна

Центры окружностей, описанных около шести треугольников, на которые произвольный треугольник разбивается своими медианами, лежат на одной окружности.

Открыта в 2000 г голандским математиком ван Ламуном. Эта магическая окружность нисколько не уступает по изяществу треугольнику Морлея. Доказательство и живая модель здесь. Говорят, этот замечательный факт был установлен с помощью Живой геометрии. См. также Квантик

Теорема Аполлония

Теорема Аполлония является формулой, выражающей длину медианы треугольника через его стороны.

Если в каком-либо треугольнике ABC медиана AD, то

Это частный случай теоремы Стюарта. Для равнобедренного треугольника теорема сводится к теореме Пифагора.

Доказательство, использующее теорему косинусов. Пусть стороны треугольника a, b, c, медиана d проведена к стороне a треугольника. Пусть m составляет половину a. Угол θ′ является смежным углом к θ и cos θ′ = −cos θ. Теорема косинусов для θ и θ′ гласит:

Сложив эти уравнения, получим $ b^+c^=2m^+2d^$

Центроид или центр масс

Все медианы треугольника пересекаются в одной точке, которая всегда находится внутри треугольника.

Эта точка обладает замечательными свойствами и называется центром тяжести или центром масс треугольника или центроидом.

Если вырезать треугольник из картона и острие карандаша воткнуть в центр масс, то его можно удержать в равновесии. Также и для любой плоской фигуры: центроид — это точка идеального баланса области, вырезанной из картона, на кончике карандаша, в предположении равномерной плотности и равномерного гравитационного поля.

Более строго: центроид может совпадать с центром масс треугольника ( = системы материальных точек: вершины треугольника с размещёнными в них массами), но только в одном частном случае — когда массы равны. При другом соотношении масс барицентр будет находиться в другой геометрической точке. При других конфигурациях материальной системы — тем более.

Медианы треугольника точкой их пересечения делятся в отношении 2:1 (считая от вершины). Геометрия, Мерзляк, 8 класс

Центроид лежит на отрезке, соединяющем ортоцентр и центр описанной окружности, и делит его в отношении 2:1 (см. прямая Эйлера).

Обобщение: центроид — геометрический центр двумерной области — среднее арифметическое позиций всех точек фигуры («средняя» точка).

Для треугольника $ABC$ в декартовых координатах центроид $M$ выражается через вершины следующим образом: $x_M = frac, y_M = frac$

У невыпуклой фигуры центроид может лежать вне фигуры (пример — кольцо).

Центроид произвольного четырёхугольника лежит в точке пересечения средних линий четырёхугольника и отрезка, соединяющего середины диагоналей, и делит все три отрезка пополам. или проще Центроид произвольного четырёхугольника лежит в точке пересечения средних линий четырёхугольника (и делит их пополам).

Четыре отрезка, каждый из которых соединяет вершину четырёхугольника с центроидом треугольника, образованного оставшимися тремя вершинами, пересекаются в центроиде четырёхугольника и делятся им в отношении 3:1, считая от вершины.

Центроид окружности совпадает с ее центром.

Видео:8 класс, 21 урок, Отношение площадей подобных треугольниковСкачать

Основные факты о треугольниках

Определения

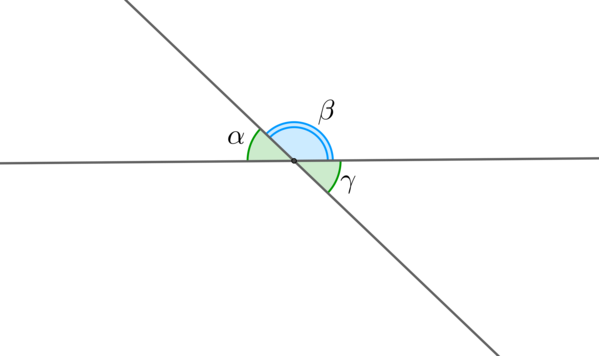
Угол – это геометрическая фигура, состоящая из точки и двух лучей, выходящих из этой точки. Градусная мера угла может принимать значения от (0^circ) до (180^circ) включительно.

Угол (alpha) называется острым, если (0^circ , прямым – если (alpha=90^circ) , тупым – если (90^circ , и развернутым – если (alpha=180^circ) .

Биссектриса угла – это луч, выходящий из вершины угла и делящий угол пополам.

Смежные углы – это два угла, у которых общая вершина и одна общая сторона, а две другие стороны образуют прямую.

Вертикальные углы – это два угла, образованные пересечением двух прямых и не являющиеся смежными.

Теорема

Смежные углы (alpha) и (beta) в сумме дают (180^circ) .

Вертикальные углы равны: (alpha=gamma) .

Определения

Треугольник – это геометрическая фигура, состоящая из трех точек, не лежащих на одной прямой (называемых вершинами треугольника), и отрезков, соединяющих эти точки (называемых сторонами треугольника). Треугольник со своей внутренностью будем сокращенно называть также треугольником.

Угол (внутренний) треугольника – угол, образованный вершиной треугольника и двумя его сторонами.

Теоремы: признаки равенства треугольников

1. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

2. Если сторона и два прилежащих угла одного треугольника соответственно равны стороне и двум прилежащим углам другого треугольника, то такие треугольники равны.

3. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

Определение

Медиана треугольника – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

Биссектриса треугольника – это отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны.

Две прямые называются перпендикулярными, если угол между ними равен (90^circ) .

Перпендикуляр из точки к прямой – это отрезок, соединяющий данную точку с точкой на прямой, проведенный под углом (90^circ) .

Высота треугольника – это перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону.

Замечание

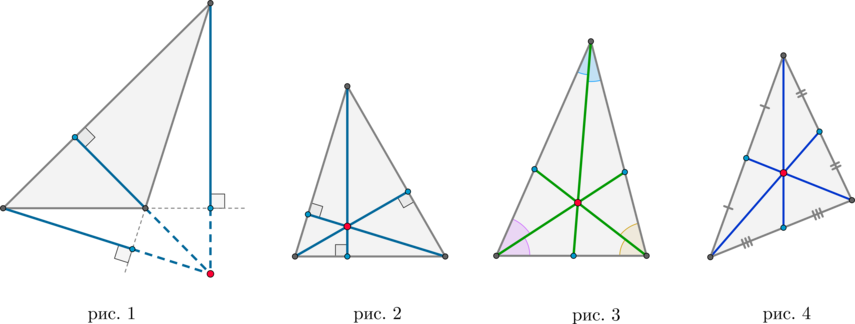
Если в треугольнике один угол тупой, то высоты, опущенные из вершин острых углов, упадут не на сторону, а на продолжение стороны (рис. 1).

Теорема

В любом треугольнике высоты (или их продолжения) пересекаются в одной точке (рис. 1 и 2), биссектрисы пересекаются в одной точке (рис. 3), медианы пересекаются в одной точке (рис. 4).

Определение

Две различные прямые на плоскости называются параллельными, если они не пересекаются.

Замечание

Заметим, что на плоскости существует три вида взаимного расположения прямых: совпадают, пересекаются и параллельны.

Аксиома параллельных прямых

Через точку, не лежащую на данной прямой, проходит единственная прямая, параллельная данной.

Следствия из аксиомы

1. Если прямая пересекает одну из параллельных прямых, то она пересекает и другую прямую.

2. Две прямые, параллельные третьей прямой, параллельны.

Теоремы: признаки параллельности прямых

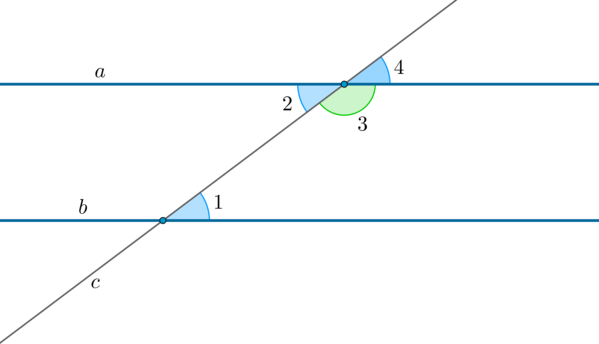
1. Если при пересечении двух прямых (a) и (b) секущей (c) накрест лежащие углы равны: (angle 1=angle 2) , то такие прямые параллельны.

2. Если при пересечении двух прямых (a) и (b) секущей (c) сумма односторонних углов (angle 1) и (angle 3) равна (180^circ) , то такие прямые параллельны.

3. Если при пересечении двух прямых (a) и (b) секущей (c) соответственные углы равны: (angle 1=angle 4) , то такие прямые параллельны.

Теоремы: свойства параллельных прямых

1. Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.

2. Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна (180^circ) .

3. Если две параллельные прямые пересечены секущей, то соответственные углы равны.

Определения

Треугольник называется остроугольным, если все его углы острые.

Треугольник называется тупоугольным, если один его угол тупой (остальные — острые).

Треугольник называется прямоугольным, если один его угол прямой (остальные — острые).

Теорема

Сумма внутренних углов треугольника равна (180^circ) .

Доказательство

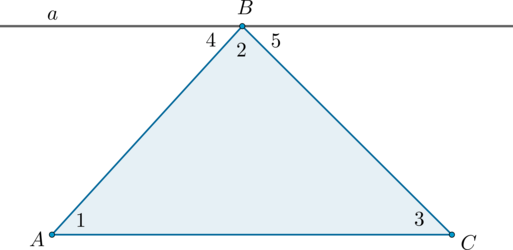
Рассмотрим произвольный треугольник (ABC) и покажем, что (angle A + angle B + angle C = 180^circ) .

Проведём через вершину (B) прямую (a) , параллельную стороне (AC) .

Углы (1) и (4) являются накрест лежащими углами при пересечении параллельных прямых (a) и (AC) секущей (AB) , а углы (3) и (5) – накрест лежащими углами при пересечении тех же параллельных прямых секущей (BC) . Поэтому [begin &angle 4 = angle 1, angle 5 = angle 3. qquad qquad qquad (1) end]

Очевидно, сумма углов (4, 2) и (5) равна развёрнутому углу с вершиной (B) , то есть (angle 4 + angle 2 + angle 5 = 180^circ) . Отсюда, учитывая равенства ((1)) , получаем: (angle 1 + angle 2 + angle 3 = 180^circ) .

Определение

Внешний угол треугольника – это угол, смежный с каким-нибудь внутренним углом треугольника.

Теорема

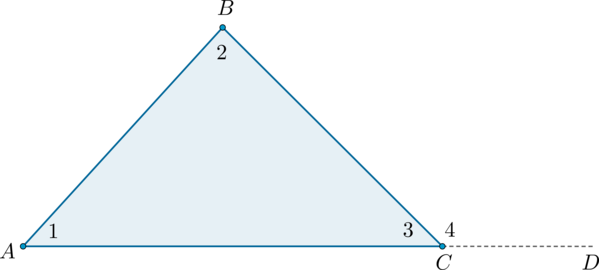
Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним: (angle BCD=angle BAC+angle ABC) .

Доказательство

Угол (4) – внешний угол треугольника, смежный с углом (3) . Так как (angle 4 + angle 3 = 180^circ) , а по теореме о сумме углов треугольника (angle 1 + angle 2 + angle 3 = 180^circ) , то (angle 4 = angle 1 + angle 2) , что и требовалось доказать.

Определения

Треугольник называется равнобедренным, если две его стороны равны.
Эти стороны называются боковыми сторонами треугольника, а третья сторона — основанием.

Треугольник называется равносторонним, если все его стороны равны.
Равносторонний треугольник, очевидно, является и равнобедренным.

Теорема

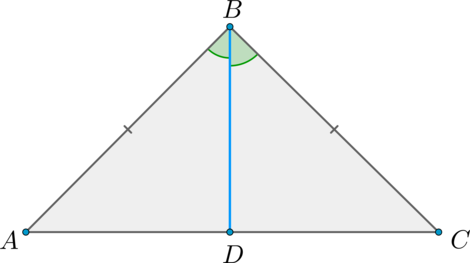
В равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и высотой.

Доказательство

Пусть (ABC) – равнобедренный треугольник, (AB = BC) , (BD) – биссектриса (проведённая к основанию).

Рассмотрим треугольники (ABD) и (BCD) : (AB = BC) , (angle ABD = angle CBD) , (BD) – общая. Таким образом, (triangle ABD = triangle BCD) по двум сторонам и углу между ними.

Из равенства этих треугольников следует, что (AD = DC) , следовательно, (BD) – медиана.

Кроме того, в равных треугольниках против равных сторон лежат равные углы, а (AB = BC) , следовательно, [begin &angle ADB = angle CDB, qquad qquad qquad (2) end] но (angle ADB + angle CDB = angle ADC) – развёрнутый, следовательно, (angle ADB + angle CDB = 180^circ) , откуда при учёте ((2)) : (angle ADB = 90^circ = angle CDB) , то есть (BD) – высота.

Верны и другие утверждения:
В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.
В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.

Теорема

В равнобедренном треугольнике углы при основании равны.

Доказательство

Проведем биссектрису (BD) (см. рисунок из предыдущей теоремы). Тогда (triangle ABD=triangle CBD) по первому признаку, следовательно, (angle A=angle C) .

Теоремы: признаки равнобедренного треугольника

1. Если в треугольнике два угла равны, то треугольник равнобедренный.

2. Если в треугольнике высота является медианой или биссектрисой, то треугольник равнобедренный.

Теорема о соотношении между сторонами и углами треугольника

В треугольнике против большей стороны лежит больший угол.

В треугольнике против большего угла лежит большая сторона.

Теорема: неравенство треугольника

В треугольнике сумма любых двух сторон больше третьей стороны.

Другая формулировка: в треугольнике разность любых двух сторон меньше третьей стороны.

Определения

В прямоугольном треугольнике большая сторона (то есть сторона, лежащая напротив прямого угла) называется гипотенузой.
Две другие стороны называются катетами.

Теоремы: свойства прямоугольного треугольника

1. Сумма острых углов прямоугольного треугольника равна (90^circ) .

2. В прямоугольном треугольнике катет, лежащий против угла (30^circ) , равен половине гипотенузы.

Верно и обратное: если катет равен половине гипотенузы, то он лежит против угла (30^circ) .

Подготовка выпускников к сдаче ЕГЭ, как правило, начинается с повторения базовой теории по планиметрии, в том числе и по теме «Треугольники». Знакомство учащихся с этим разделом геометрии начинается еще в средней школе. Неудивительно, что потребность в повторении основных правил и теории по теме «Треугольник» возникает у многих выпускников. При этом решать планиметрические задачи обязательно должны уметь все учащиеся. Подобные задания включены как в базовый, так и в профильный уровень аттестационного испытания. Разобравшись с теорией и практическими упражнениями, в том числе и на вычисление вертикальных углов треугольника, старшеклассники смогут решать задачи с любым количеством действий и рассчитывать на получение конкурентных баллов по итогам сдачи ЕГЭ.

Видео:Треугольники. 7 класс.Скачать

Готовьтесь к экзамену вместе с образовательным порталом «Школково»

Занимаясь перед сдачей ЕГЭ, многие учащиеся сталкиваются с проблемой поиска базовой теории по геометрии о треугольниках. Школьных учебников в нужный момент может просто не оказаться под рукой. А найти необходимые формулы иногда оказывается достаточно сложно даже в Интернете.

Вместе с образовательным порталом «Школково» выпускники смогут качественно подготовиться к сдаче аттестационного испытания. Вся базовая теория о равнобедренных и прямоугольных треугольниках систематизирована и изложена нашими специалистами с учетом богатого опыта в максимально доступной форме. Изучив представленную информацию, школьники смогут вспомнить материал, который вызывает определенные затруднения.

Чтобы хорошо подготовиться к экзамену, учащимся, проживающим в Москве и других городах России, необходимо не только повторить теорию о прямоугольных и равнобедренных треугольниках, но и попрактиковаться в выполнении соответствующих упражнений. Задачи по данной теме вы можете найти в разделе «Каталог». Для каждого задания наши специалисты прописали подробный ход решения и указали правильный ответ. Последовательно выполняя простые и более сложные упражнения по данной теме, учащиеся смогут научиться применять на практике теоремы равенства треугольников и другую теорию, которую необходимо усвоить при подготовке к ЕГЭ. Перечень заданий в соответствующем разделе постоянно дополняется и обновляется.

Попрактиковаться в решении задач, в которых применяется теория смежных углов и другие теоремы, школьники могут в режиме онлайн.

По желанию учащегося любое упражнение можно сохранить в «Избранное». Еще раз повторив базовую теорию о прямоугольных и равнобедренных треугольниках, выпускник может в дальнейшем вернуться к заданию, которое вызвало затруднения, и обсудить алгоритм его решения с преподавателем.