Доказать треугольник abm равен kpb

Геометрия как отдельный предмет начинается у школьников в 7 классе. До этого времени они касаются геометрических задач достаточно лёгкой формы и в основном того, что можно рассмотреть на наглядных примерах: площади комнаты, земельного участка, длины и высоты стен в помещениях, периметра плоских предметов и прочее. В нача ле изучения непосредственно геометрии появляются первые сложности, такие, например, как понятие прямой, так как потрогать руками эту прямую нет возможности. Что касается треугольников -это самый простой вид многоугольников, содержащий всего три угла и три стороны.

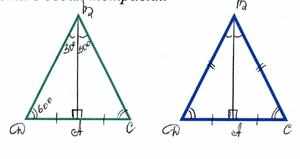
Тема треугольников одна из основных важных и больших тем школьной программы в геометрии 7−9 классов. Усвоив её хорошо, возможно решать очень сложные задачи. При этом можно изначально рассматривать совершенно другую геометрическую фигуру, а затем разделить её для удобства на подходящие треугольные части.

Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Как доказать, что треугольники равны

Для работы над доказательством равенства ∆ ABC и ∆A1B1C1 нужно хорошо усвоить признаки равенства фигур и уметь ими пользоваться. Перед изучением признаков необходимо научиться определять равенство сторон и углов простейших многоугольников.

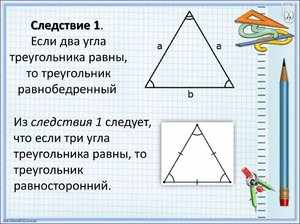
Чтобы доказать, что углы треугольников равны, помогут следующие варианты:

1. ∠ α = ∠ β исходя из построения фигур.
2. Дано в условии задания.
3. При двух параллельных прямых и наличии секущей могут образоваться как внутренние накрест лежащие, так и соответственные ∠ α = ∠ β.
4. Прибавляя (вычитая) к (из) ∠ α = ∠ β равные углы.
5. Всегда сходны вертикальные ∠ α и ∠ β
6. Общий ∠ α, одновременно принадлежащий ∆ MNK и ∆ MNH .
7. Биссектриса делит ∠ α на два равнозначных.
8. Смежный с ∠ 90° — угол, равный исходному.
9. Смежные равным углам равны.
10. Высота образует два смежных ∠ 90° .
11. В равнобедренном ∆ MNK при основании ∠ α = ∠ β.
12. В равных ∆ MNK и ∆ SDH соответствующие ∠ α = ∠ β.
13. Доказанное ранее равенство ∆ MNK и ∆ SDH .

Как же доказать, что треугольники подобны? Достаточно воспользоваться одним из выше перечисленных признаков и грамотно описать весь процесс доказательства задания. Тема подобия ∆ MNK и ∆ SDH проще воспринимается школьниками исходя из того, что к моменту её изучения ученики уже свободно пользуются обозначениями элементов в геометрических построениях, не путаются в огромном количестве названий и умеют читать чертежи.

Завершая прохождение обширной темы треугольных геометрических фигур, учащиеся уже в совершенстве должны знать, как доказать равенство ∆ MNK = ∆ SDH по двум сторонам, установить равны два треугольника или нет. Учитывая, что многоугольник, имеющий ровно три угла — это одна из важнейших геометрических фигур, к усвоению материала следует подойти серьёзно, уделяя особое внимание даже мелким фактам теории.

Видео:7 класс, 15 урок, Первый признак равенства треугольниковСкачать

Докажите равенство треугольников ABM и CD(рис?

Геометрия | 5 — 9 классы

Докажите равенство треугольников ABM и CD(рис.

46), если AM = CM и угоBAM = углу DCM.

AM = CM(по условию)

угол BAM = углу DCM(по условию)

из этого следует, что треугольники равны по двум углам и стороне между ними.

Видео:7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать

Докажите признак равенства равнобедренных треугольников по основанию и углу при основании?

Докажите признак равенства равнобедренных треугольников по основанию и углу при основании.

Видео:к. р. геометрия ТреугольникиСкачать

Равнобедренном треугольнике ABC с основанием AC на медиане BD выбрана точка M?

Равнобедренном треугольнике ABC с основанием AC на медиане BD выбрана точка M.

Докажите равенство треугольника ABM и CBM.

Видео:№119. В равнобедренном треугольнике DEK с основанием DK=16см отрезок EF— биссектриса,Скачать

Докажите равенство прямоугольных треугольников по острому углу и высоте, опущенной на гипотенузу?

Докажите равенство прямоугольных треугольников по острому углу и высоте, опущенной на гипотенузу.

Видео:№142. Равнобедренные треугольники ADC и BCD имеют общее основание DC. Прямая АВ пересекает отрезокСкачать

Докажите признак равенства равнобедренных треугольников по основанию и углу при основании?

Докажите признак равенства равнобедренных треугольников по основанию и углу при основании.

Видео:№161. В треугольниках ABC и А1B1С1 медианы AM и А1М1 равны, BC=B1С1 и ∠AMB=∠A1M1B1. Докажите, чтоСкачать

Докажите признак равенства равнобедренных треугольников по основанию и углу при основании?

Докажите признак равенства равнобедренных треугольников по основанию и углу при основании.

Видео:Периметр треугольника. Как найти периметр треугольника?Скачать

Точка M — СЕРЕДИНА БОКОВОЙ стороны BC Трапеции ABCD?

Точка M — СЕРЕДИНА БОКОВОЙ стороны BC Трапеции ABCD.

Докажите что площадь трапеции вдвое больше суммы площадей треугольнков ABM И DCM.

Видео:Профиль ОБЪЕМА и УРОВНИ за 10 минут⏱ Обучение СТРАТЕГИИ + ИндикаторСкачать

Докажите равенство прямоугольниках треугольников по гипотенузе и острому углу ?

Докажите равенство прямоугольниках треугольников по гипотенузе и острому углу ?

Видео:№127. В треугольнике ABC сумма углов A и B равна 90°. Прямая BD перпендикулярна к плоскостиСкачать

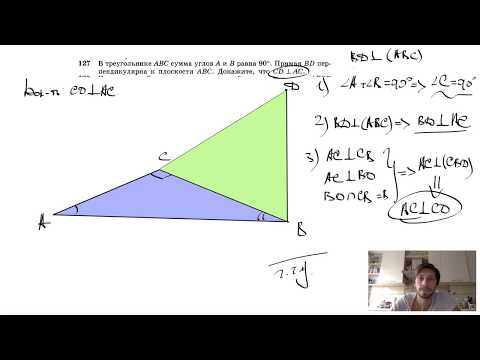
Докажите признак равенства треугольников по высоте и двум углам, на которые она делит угол треугольника?

Докажите признак равенства треугольников по высоте и двум углам, на которые она делит угол треугольника.

Видео:№118. На основании ВС равнобедренного треугольника ABC отмечены точки М и N так, что BM=CN. ДокажитеСкачать

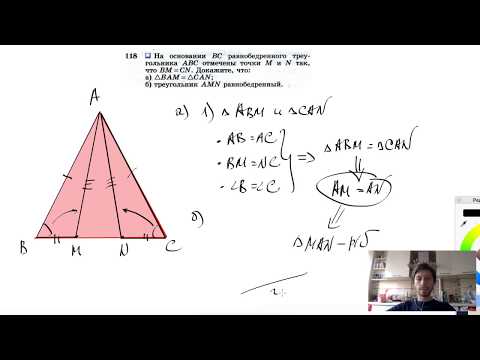
Докажите равенство прямоугольных треугольников по гипотенузе и острому углу?

Докажите равенство прямоугольных треугольников по гипотенузе и острому углу.

Видео:№109. В равнобедренном треугольнике ABC с основанием ВС проведена медиана AM. Найдите медиану AMСкачать

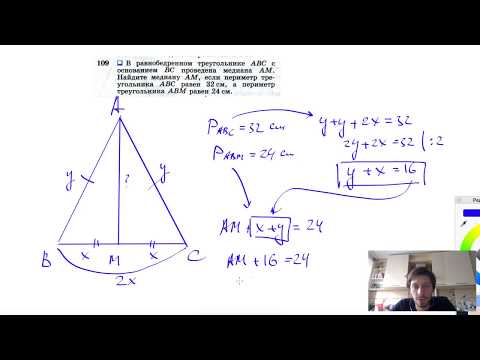
Докажите равенство двух треугольников по стороне, прилегающим к ней углом и биссектрисой этого угла?

Докажите равенство двух треугольников по стороне, прилегающим к ней углом и биссектрисой этого угла.

Вы находитесь на странице вопроса Докажите равенство треугольников ABM и CD(рис? из категории Геометрия. Уровень сложности вопроса рассчитан на учащихся 5 — 9 классов. На странице можно узнать правильный ответ, сверить его со своим вариантом и обсудить возможные версии с другими пользователями сайта посредством обратной связи. Если ответ вызывает сомнения или покажется вам неполным, для проверки найдите ответы на аналогичные вопросы по теме в этой же категории, или создайте новый вопрос, используя ключевые слова: введите вопрос в поисковую строку, нажав кнопку в верхней части страницы.

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Презентация по геометрии на тему «Второй признак равенства треугольников»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

Второй признак равенства треугольников

Какая фигура называется треугольником? Какие треугольники называются равными? Как можно узнать, равны ли данные треугольники? Какие элементы достаточно рассмотреть для доказательства равенства треугольников?

Первый признак равенства треугольников. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

Второй признак равенства треугольников. Если сторона и два прилежащие к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

Тест: 1. Для доказательства равенства треугольников АВС и MNK достаточно доказать, что: а) АС = MN; б) ∠C = ∠N; в) BC = MK. 2. Для доказательства равенства треугольников АСВ и EDF достаточно доказать, что: а) AC = FE; б) ∠C = ∠E; в) ∠A = ∠F. 3. Чтобы доказать равенство равносторонних треугольников АВС и MNK, достаточно доказать, что: а) ∠А = ∠М; б) АВ = МN; в) PABC = PMNK. 4. Чтобы доказать равенство двух равнобедренных треугольника TOS и DEF с основаниями TS и DF, достаточно доказать, что: а) ∠О = ∠Е; б) TS = DF и ∠Т = ∠D; в) TS = DF. 5. Выберите верное утверждение: а) ВС = КN; б) АВ = КN; в) ВС = NM. C A B K N M A B C F D E A B C M N K

Ответы: 1.в) 2.б) 3.б) 4.б) 5.а)

Задача № 1. Отрезки AB и CD пересекаются в точке O. Докажите равенство треугольников ACO и DOB если известно, что угол ACO равен углу DBO и BO=CO.

Решение: Рассмотрим ∆ ACO и ∆ DBO: BO=CO (по условию)

Отрезки AC и BD пересекаются в точке O. Докажите равенство треугольников BAO и DCO, если известно, что угол BAO равен углу DCO, AO = CO. Задача № 2.

Решение: Рассмотрим ∆ BAO и ∆ DCO. AO = CO (по условию)

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 976 человек из 78 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 308 человек из 70 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 677 человек из 74 регионов

Ищем педагогов в команду «Инфоурок»

Видео:Теорема о точке пересечения медиан треугольника. Доказательство. 8 класс.Скачать

Дистанционные курсы для педагогов

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 550 540 материалов в базе

Другие материалы

• 30.11.2015
• 463
• 1

• 30.11.2015
• 465
• 1

• 30.11.2015
• 1297
• 13

• 30.11.2015
• 650
• 1

• 30.11.2015
• 316
• 0

• 30.11.2015
• 577
• 0

• 30.11.2015
• 598
• 0

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 30.11.2015 5118
• PPTX 149 кбайт
• 5 скачиваний
• Оцените материал:

Настоящий материал опубликован пользователем Козулина Александра Вячеславовна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 6 лет и 2 месяца
• Подписчики: 1
• Всего просмотров: 66151
• Всего материалов: 8

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:№140. В треугольниках ABC и А1B1С1 медианы ВМ и B1М1 равны, АВ =А1B1, АС=А1С1. Докажите, что ΔABCСкачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Власти Бурятии заявили о нехватке школьных учителей и воспитателей

Время чтения: 2 минуты

У 76% российских учителей оклад ниже МРОТ

Время чтения: 2 минуты

Полный перевод школ на дистанционное обучение не планируется

Время чтения: 1 минута

Общество «Знание» в 2022 году планирует запустить серию хакатонов и школу лекторов

Время чтения: 2 минуты

В Рособрнадзоре рассказали, как будет меняться ЕГЭ

Время чтения: 2 минуты

Петербургская учительница уволилась после чтения на уроке Введенского и Хармса

Время чтения: 3 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

🎥 Видео

Высота, биссектриса, медиана. 7 класс.Скачать

Теорема о свойстве медианы равнобедренного треугольникаСкачать

№539. В треугольник MNK вписан ромб MDEF так, что вершины D, Е и F лежат соответственноСкачать

7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

В треугольнике ABC проведена медиана BM, на стороне AB взята точка K так, что AK = 1/3 AB. РЕШЕНИЕ!Скачать