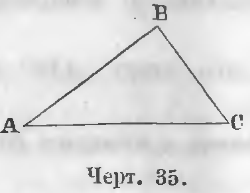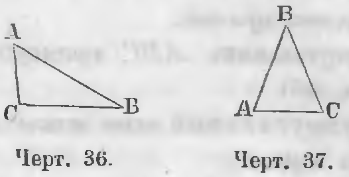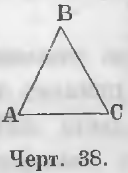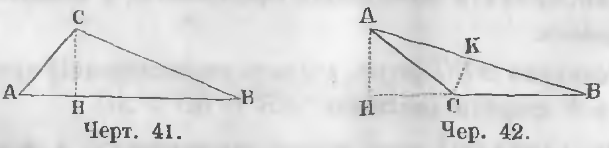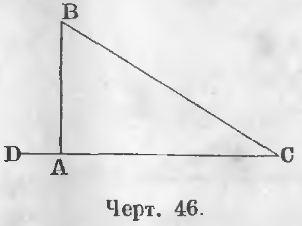Доказать треугольник abc треугольнику bcd

Видео:№127. В треугольниках ABC и А1В1С1 АВ=А1В1, ВС=В1С1, ∠B =∠B1Скачать

Ваш ответ

Видео:№142. Равнобедренные треугольники ADC и BCD имеют общее основание DC. Прямая АВ пересекает отрезокСкачать

Похожие вопросы

• Все категории
• экономические 43,283
• гуманитарные 33,619
• юридические 17,900
• школьный раздел 607,084
• разное 16,829

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:ОГЭ Р-2 номер 16Скачать

Математика

Треугольник есть определенная часть плоскости, ограниченная тремя взаимно пересекающимися прямыми линиями.

Стороны треугольника. Прямые линии, ограничивающие треугольник, называются сторонами треугольника.

Каждые две пересекающиеся прямые образуют угол треугольника.

Три пересекающиеся стороны образуют три угла треугольника.

Вершины. Точки пересечения сторон называются вершинами треугольника.

На чертеже 35 имеем треугольник ABC, три стороны AB, BC и AC, три угла BAC, ABC и BCA и три вершины A, B, C. Для сокращения слово треугольник изображают иногда знаком ∆ .

Треугольники получают различные названия, смотря по взаимному отношению его сторон и по углам, его составляющим.

Разделение треугольников по отношению к сторонам. По отношению к сторонам треугольники делятся на треугольники разносторонние, равнобедренные и равносторонние.

Разносторонний есть такой треугольник, у которого все стороны не равны.

Треугольник ABC (черт. 36) есть разносторонний треугольник. У него все стороны различны: AB > BC > AC.

Равнобедренный есть такой треугольник, у которого две стороны равны. На черт. 37 ABC есть равнобедренный треугольник. У него две стороны AB и BC равны (AB = BC).

Равносторонний есть такой треугольник, у которого все три стороны равны.

Треугольник ABC (черт. 38) равносторонний, ибо у него все стороны равны: AB = BC = AC.

Разделение треугольников по отношению к углам. По отношению к углам треугольники разделяются на остроугольные, прямоугольные и тупоугольные.

Остроугольный есть такой треугольник, у которого все три угла острые.

Треугольник ABC (черт. 39) есть остроугольный, ибо все его три угла A, B, C острые.

Прямоугольный есть такой треугольник, у которого один из углов прямой.

Треугольник ABC прямоугольный, ибо угол ABC прямой (черт. 40).

Тупоугольный есть такой треугольник, у которого один из углов тупой.

Треугольник ABC (черт. 36) тупоугольный, ибо угол ACB тупой.

В каждом треугольнике можно выбрать какую-нибудь сторону за основание, тогда перпендикуляр, опущенный из противоположной вершины на основание, называется высотою треугольника.

Высота есть расстояние вершины от основания треугольника, считаемое по перпендикуляру. Высота есть длина перпендикуляра, опущенного из вершины на основание.

Если на чертеже 41 примем линию AB за основание, то линия CH будет высотой треугольника. Если примем на чертеже 42 за основание линию BC, то высотой будет линия AH. Если бы за основание была выбрана линия AB, то высотой была бы линия CK.

Свойство сторон треугольника. Во всяком треугольнике каждая сторона меньше суммы и больше разности двух других сторон.

Так, в треугольнике ABC (черт. 35)

AC AC — BC
BC > AB — AC
AC > BC — AB

Равные треугольники. Два треугольника называются равными, если при наложении друг на друга они совмещаются всеми своими точками.

Видео:7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать

Равенство треугольников

Теорема 19. Два треугольника равны, если три стороны одного соответственно равны трем сторонам другого.

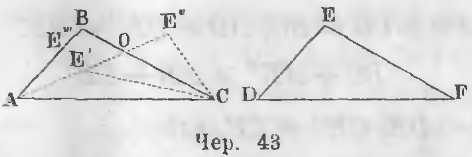
Дано. В двух треугольниках ABC и DEF (черт. 43) стороны равны

AB = DE, BC = EF, AC = DF

Требуется доказать, что ∆ ABC = ∆ DEF.

Доказательство. Наложим треугольник DEF на треугольник ABC, сторону DF на сторону AC точкой D на точку A. По равенству сторон AC и DF точка F упадет на точку C.

Чтобы доказать, что точка E упадет на точку B докажем, что она не может упасть ни внутри, ни вне, ни на одну из сторон треугольника.

a) Положим, что точка E упадет внутри треугольника в точку E’, тогда треугольник DEF примет положение треугольника AE’C, DE займет положение линии AE’ и EF положение линии E’C, следовательно,

Линия ABC, будучи внешней ломаной, больше линии AE’C внутренней ломаной, следовательно,

Заменяя AE’ и E’C равными им сторонами DE и EF, имеем:

но AB = DE, следовательно, BC > EF, что противоречит данным условиям. Итак, точка E не может упасть внутри треугольника.

b) Положим, точка E упала вне треугольника в точку E». В этом случае ∆AE»C = ∆DEF и тогда

Обозначим букой O точку пересечения линий AE» и BC. Из чертежа видно, что

AO + BO > AB
CO + OE» > E»C

Сложив эти неравенства, имеем:

AO + BO + CO + OE» > AB + E»C

Так как BO + CO = BC, AO + OE» = AE», то

Здесь AE» = DE, CE» = EF, следовательно,

Вычтя по равной величине из обоих частей последнего неравенства, получаем:

что противоречит данным условиям. Итак, точка E не может упасть вне треугольника.

c) Точка E не может упасть на одну из сторон треугольника в точку E»’, ибо стороны DC и AB равны. Точно также если бы E упала в точку O, то выходило бы, что BC > OC, но OC = EF, следовательно, BC > EF, что противоречит условию.

Итак, точка E должна непременно упасть в точку B, следовательно, при наложении сторона DE совпадет со стороной AB, а сторона EF со стороной BC и треугольник DEF с треугольником ABC.

Из равенства треугольников следует, что все остальные части их равны, т. е.

Теорема 20. Два треугольника равны, когда они имеют по равному углу, содержащемуся между равными сторонами.

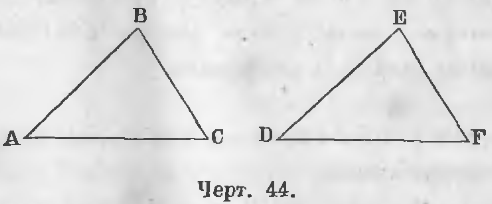
Дано. В двух треугольниках ABC и DEF (черт. 44)

AB = DE, AD = DF, ∠BAC = ∠EDF

Требуется доказать, что ∆ABC = ∆DEF.

Примечание. Иногда указывают равные части на чертеже, отмечая их одинаковыми значками.

Доказательство. Наложим треугольник DEF на треугольник ABC, сторону DF на сторону AC, точкой D на точку A; тогда по равенству линий DF и AC точка F упадет в точку C и по равенству углов A и D линия DE пойдет по линии AB; по равенству линий DE и AB точка E упадет на точку B. Если E и F две точки линии EF совпали с B и C двумя точками линии BC, то и вся линия EF совпадет с линией BC, и треугольник DEF совпадет с треугольником ABC. Отсюда следует, что и все остальные части треугольников равны, т. е.

BC = EF, ∠B = ∠E, ∠C = ∠F.

Теорема 21. Два треугольника равны, если сторона и два лежащие на ней угла одного равны стороне и двум лежащим на ней углам другого треугольника.

Дано. В треугольниках ABC и DEF (черт. 44)

∠ A = ∠D, ∠C = ∠F, AC = DF

Требуется доказать, что ∆ABC = ∆DEF.

Доказательство. Наложим треугольник DEF на треугольник ABC, стороной DF на AC, точкой D на A, тогда по равенству сторон AC и DF точка F упадет на точку C. По равенству углов A и D линия DE пойдет по линии AB и по равенству углов C и F линия FE пойдет по линии CB. Так как линия FE и DE совпадут с линиями CB и AB, то и точка E непременно совпадет с точкой B, ибо две прямые линии пересекаются в одной точке, следовательно два треугольника равны (ЧТД).

Из того, что равные треугольники совмещаются при наложении всеми своими частями вытекает следствие. В равных треугольниках против равных сторон лежат равные углы и наоборот.

Соответственные части треугольников. В двух равных треугольниках равные углы и равные стороны называются соответственными углами и сторонами.

Видео:№111. На рисунке 65 CD = BD, ∠1=∠2. Докажите, что треугольник ABC равнобедренный.Скачать

Внешний угол треугольника

Внешний угол треугольника есть всякий угол смежный с углом треугольника.

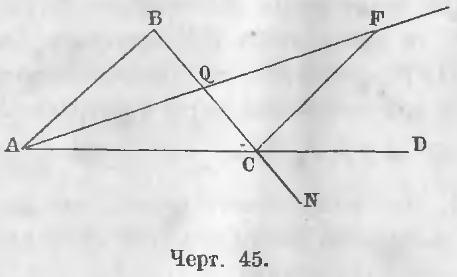
Так, на чертеже 45, угол BCD есть внешний угол.

Теорема 22. Во всяком треугольнике внешний угол больше каждого внутреннего не смежного с ним.

Дан внешний угол BCD (черт. 45).

Требуется доказать, что BCD > A и BCD > B.

Доказательство. Точку Q середину линии BC соединим с A и отложим на продолжении линии AQ линию QF равную AQ.

Соединим F с C; тогда два треугольника ABQ и QFC равны, ибо имеют по равному углу, лежащему между двумя равными сторонами.

Действительно, по построению BQ = QC, AQ = QF, а углы BQA и FQC равны как вертикальные, следовательно,

Если линия AQ = QF, то и ∠ABC = ∠BCF.

Угол BCD > угла BCF, следовательно, и угол BCD > ABC.

Производя подобное же построение, мы могли бы доказать, что угол ACN > угла BAC.

Так как ACN = BCD, то и угол BCD > угла BAC.

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Прямоугольный треугольник

Следствие 1. В прямоугольном треугольнике из трех углов один прямой, а другие два острые.

Доказательство. Внешний угол BAD прямоугольного треугольника ABC (черт. 46) больше внутренних углов B и C, следовательно, оба угла B и C острые.

Гипотенуза. Сторона прямоугольного треугольника, лежащая против прямого угла, называется гипотенузой.

Катеты. Стороны прямоугольного треугольника, лежащие против острых углов, называются катетами.

Сторона BC есть гипотенуза, а стороны AB и AC катеты (черт. 46).

Гипотенуза больше каждого из катетов и меньше суммы двух катетов, ибо гипотенуза наклонная, а катеты перпендикулярны.

Видео:№171. В треугольниках ABC и ADC стороны ВС и AD равны и пересекаются в точке О, ∠OAC=∠OCA. ДокажитеСкачать

Тупоугольный треугольник

Следствие 2. В тупоугольном треугольнике один угол тупой, а два остальные угла острые.

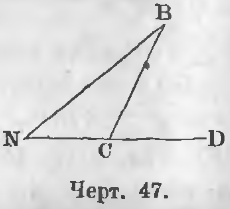
Доказательство. В тупоугольном треугольнике NBC (черт. 47) угол NCB тупой. Продолжая сторону NC, мы находим внешний острый угол BCD. Так как BCD > N и BCD > B, то оба угла N и B тупоугольного треугольника острые. Отсюда делаем заключение : в треугольнике не может быть более одного прямого и более одного тупого угла .

Теорема 23 . Если две стороны одного треугольника равны двум сторонам другого, а углы, заключающиеся между этими сторонам не равны, то против большего угла лежит большая сторона.

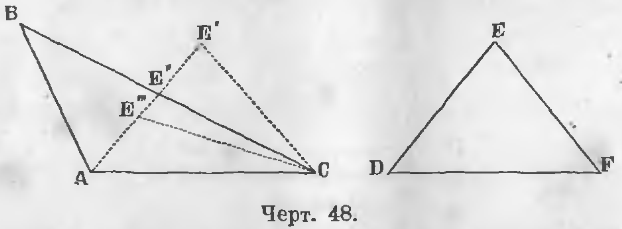
Дано. В двух треугольниках ABC и DEF (черт. 48)

AC = DF, AB = DE, угол BAC > угла EDF.

Требуется доказать, что BC > EF.

Доказательство . Наложим треугольник DEF на ABC, стороной DF на AC, точкой D на A. Точка F по равенству сторон DF и AC совпадет с C.

Так как D меньше угла A, то сторона DE пойдет по направлению AE’.

Здесь могут быть три случая: точка E может упасть вне, на сторону и внутри треугольника ABC, т. е. в точках E’, E» и E»’.

1) 1-й случай . Когда точка E упадет в E’, треугольник DEF займет положение треугольника AE’C, следовательно,

AE’ = DE = AB
E’C = EF

Не трудно заметить, что

AE» + E»B > AB
CE» + E»E’ > CE’

Сложив эти неравенства, получим:

AE» + E»B + CE» + E»E’ > AB + CE’

AE» + E»E = AE’
CE» + E»B = BC

Здесь AE’ = AB, следовательно,

BC > CE’ или
BC > EF (ЧТД).

2) 2-й случай . Точка E упадет в E», тогда E»C = EF и

BC > E»C, а следовательно, BC > EF.

3) 3-й случай . Точка E упадет в E»’. В этом случае

По свойству ломаных (теорема 1)

AB + BC > AE»’ + E»’C или
AB + BC > DE + EF.

Так как AB = DE, то последнее неравенство дает

Итак во всех трех случаях BC > EF (ЧТД).

Теорема 24 . (Обратная 23). Если две стороны одного треугольника равны двум сторонам другого, а третьи стороны не равны, то против большей стороны лежит больший угол.

Дано. В треугольниках ABC и DEF (черт. 48) AB = DE, AC = DF и BC > EF.

Требуется доказать, что угол BAC > угла EDF.

Доказательство . Здесь могут быть только три предположения: угол BAC может быть равен, меньше или больше угла EDF.

1) Если бы угол BAC равнялся углу EDF, то два треугольника ABC и EDF были бы равны (теорема 20). В этом случае сторона BC равнялась бы стороне EF, что противоречит условию.

2) Если бы угол BAC был меньше угла EDF, то по предыдущей теореме и сторона BC была бы меньше EF, что также противоречит условию; следовательно, угол BAC больше угла EDF (ЧТД).

Видео:7 класс, 15 урок, Первый признак равенства треугольниковСкачать

Взаимное отношение углов и сторон в треугольнике

Теорема 25 . В равнобедренном треугольнике против равных сторон лежат равные углы.

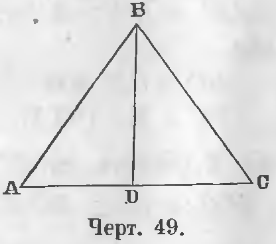
Дан равнобедренный треугольник ABC (черт. 49), т. е. треугольник, у которого AB = BC.

Требуется доказать, что ∠ A = ∠ C.

Доказательство . Соединим точку B с точкой D, которая является серединой стороны AC.

Два треугольника ABD и BDC равны, ибо имеют по три равных стороны. Действительно:

BD — общая сторона;
AD = DC по построению (D середина отрезка AC);
AB = BC по условию.

В равных треугольниках против равных сторон лежат равные углы, следовательно,

Теорема 26 (обратная 25). В треугольнике против равных углов лежат равные стороны .

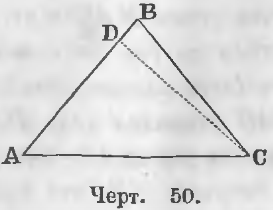
Дано. В треугольнике ABC ∠ A = ∠ C (черт. 50).

Требуется доказать, что AB = BC.

Доказательство . Положим, сторона AB > BC. Тогда, отложив на стороне AB часть AD равную BC, имеем два треугольника ADC и ABC, у которых

AC — общая сторона,
AD = BC по построению,
∠ A = ∠ C по условию.

Таким образом, AC и AD, две стороны треугольника ADC и уголь между ними A соответственно равны AC и BC, двум сторонам треугольника ABC, и углу C между ними. При этих условиях треугольники ADС и ABC были бы равны, что очевидно несообразно, ибо ∆ADC

Теорема 27 . В треугольнике против большего угла лежит большая сторона .

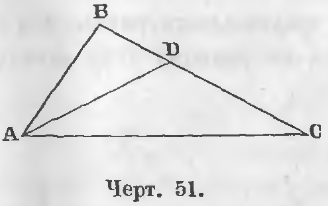
Дано. В треугольнике ABC (черт. 51) ∠ A > ∠ C.

Т ребуется доказать, что BC > AB.

Доказательство . Построим при точке A угол DAC равный углу C, тогда в треугольнике BDA

В равнобедренном треугольнике ADC

следовательно, предыдущее неравенство примет вид

Теорема 28 (обратная 27). В треугольнике против большей стороны лежит больший угол .

Дано. В треугольнике ABC (черт. 51) BC > AB.

Требуется доказать, что ∠ BAC = ∠ BCA.

Доказательство . a) Угол A не может быть равен углу C, ибо тогда сторона AB равнялась бы стороне BC (теорема 26).

b) Угол A не может быть меньше C, ибо тогда сторона BC была бы меньше AB (теорема 27), следовательно, BC > AB (ЧТД).

Видео:№118. На основании ВС равнобедренного треугольника ABC отмечены точки М и N так, что BM=CN. ДокажитеСкачать

Равенство прямоугольных треугольников

Так как у прямоугольных треугольников прямые углы равны, то для равенства их требуется меньше условий.

Теорема 29 . Два прямоугольных треугольника равны, когда две стороны одного равных двум сторонам другого.

Здесь имеют место два случая:

A) Когда два катета одного равны двум катетам другого и

B) Когда они имеют по равному катету и равной гипотенузе .

Разберем эти два случая отдельно.

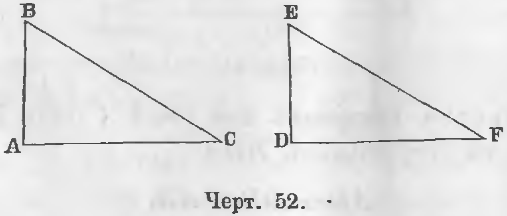
A) Прямоугольные треугольника ABC и DEF (черт. 52) имеют равные катеты

В этом случае треугольники равны, ибо они имеют по двум равным сторонам и по равному углу между ними.

B) Прямоугольные треугольники ABC и DEF имеют по равному катету и равной гипотенузе, следовательно, BC = EF, DE = AB (черт. 52).

Доказательство . Наложим треугольник DEF на ABC, катет DE на AB, точку D на A. По равенству линий AB и DE точка E упадет на точку B. По равенству прямых углов A и D линия DF пойдет по линии AC. Отрезки EF и BC как равные наклонные находятся на равных расстояниях от перпендикуляра, следовательно, расстояние DF и AC равны и отрезок EF пойдет по отрезку BC.

Теорема 30 . Два прямоугольных треугольника равны, если они имеют по равной стороне и равному соответственному углу.

Здесь тоже имеют место два случая:

A) Когда прямоугольные треугольники имеют по равному катету и равному острому углу и B) когда они имеют по равной гипотенузе и равному острому углу .

Рассмотрим эти два случая отдельно:

A) Если прямоугольные треугольники имеют по равному катету и равному острому углу, то острый угол может быть a) прилежащий или b) противолежащий.

a) Прямоугольные треугольники имеют по равному катету и равному прилежащему острому углу, т. е.

DE = AB и ∠ E = ∠ B (черт. 52).

В этом случае треугольники равны, ибо они имеют по равной стороне и равным двум лежащим на ней углам.

b) Прямоугольные треугольники имеют по равному катету и по равному противоположному острому углу, т. е.

DE = AB, ∠ C = ∠ F (черт. 52).

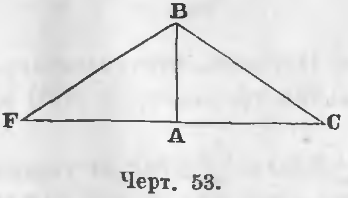
Повернуть треугольник DEF около оси DE и приставив сторону DE к стороне AB так, чтобы он занял положение ABF (черт. 53), получим равнобедренный треугольник FBC, ибо ∠ F = ∠ C, следовательно, наклонные BF и BC тоже равны и находятся на равных расстояниях AF и AC от перпендикуляра AB, т. е. два треугольника ABF и ABC равны, а следовательно равны и треугольники ABC и DEF (ЧТД).

B) Прямоугольные треугольники имеют по равной гипотенузе и равному острому углу, т. е.

BC = EF, ∠ C = ∠ F (черт. 52)

Доказательство . Наложим треугольник DEF на ABC, сторону DF на AC, точку F на C. По равенству углов F и C линия FE пойдет по линии BC и по равенству отрезков EF и BC точка E упадет на точку B. Линия ED непременно пойдет по линии BA, ибо обе линии ED и BA перпендикулярны к линии AC, а из точки на прямую линию можно опустить только один перпендикуляр, следовательно, треугольник DEF совпадет с треугольником ABC во всех своих частях (ЧТД).

Теорема 31 . Все точки биссектрисы угла находятся на равном расстоянии от его сторон.

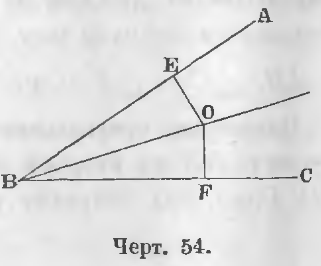
Дан угол ABC (черт. 54) и биссектриса BO, следовательно

Требуется доказать, что для какой-нибудь точки O перпендикуляры OE и OF равны.

Доказательство . Опустив перпендикуляры OE и OF, находим, что прямоугольные треугольники BEO и BFO равны, ибо BO сторона общая

∠ EBO = ∠ FBO по условию,
следовательно, EO = FO (см. теорему 30) (ЧТД).

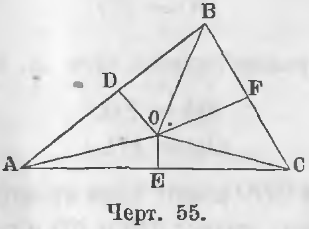
Теорема 32 . Перпендикуляры, восставленные из середины сторон треугольника, пересекаются в одной точке .

Дан треугольник ABC (черт. 55), O есть точка пересечения перпендикуляров DO и EO, восставленных из середин сторон AB и AC, следовательно,

Требуется доказать, что точка O находится на перпендикуляре, восставленном из середины третьей стороны BC.

Доказательство . Соединим точку O с вершинами треугольника ABC отрезками AO, BO, CO.

Точка O находится на перпендикуляре восставленном из середины отрезка AC (теорема 17), следовательно, AO = CO.

Точка O находится на перпендикуляре, восставленном из середины отрезка AB, следовательно, AO = BO.

Откуда BO = CO, т. е. точка O находится на равном расстоянии от концов отрезка BC, следовательно, она находится на перпендикуляре FO, восставленном из середины отрезка BC (ЧТД).

Точка O называется центром описанного круга .

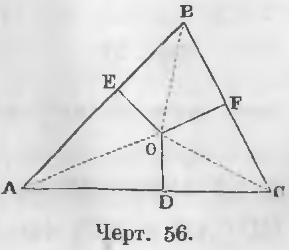
Теорема 33 . Биссектрисы трех углов треугольника пересекаются в одной точке.

Даны линии AO и BO — биссектрисы углов A и B треугольника ABC и точка O (черт. 56) их точка пересечения, следовательно,

∠ BAO = ∠ CAO, ∠ ABO = ∠ CBO.

Требуется доказать, что линия OC будет тоже биссектрисой угла C.

Доказательство . Опустим из точки O перпендикуляры OD, OE, OF на стороны треугольника.

Из того, что AO биссектриса угла A, следует (теорема 31), что

Из того, что BO биссектриса угла B, следует, что

Треугольники CFO и CDO равны, как прямоугольные треугольники, имеющие по равному катету DO и FO и гипотенузе CO (теорема 29), откуда

Следовательно, прямая CO есть биссектриса угла BCA (ЧТД).

Видео:№115. Медиана AM треугольника ABC равна отрезку ВМ. Докажите, что один из углов треугольника ABCСкачать

Доказать треугольник abc треугольнику bcd

Вопрос по геометрии:

1. Угол C треугольника ABC- прямой. AD- перпендикуляр к плоскости треугольника ABC. Докажите, что треугольник BCD- прямоугольный.

2. Из вершины A квадрата ABCD со стороной 16 см восстановлен перпендикуляр AE длиной 12 см. докажите, что треугольник BCE- прямоугольный. Найдите его площадь.

3. Отрезок AM перпендикулярен плоскости треугольника ABC и имеет длину 24 см. Найдите расстояние от точки M до прямой BC, если AB=AC=20 см., BC=24 см.

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!

Ответы и объяснения 1

Угол C треугольника ABC- прямой. AD- перпендикуляр к плоскости треугольника ABC. Докажите, что треугольник BCD- прямоугольный.

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

• Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
• Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
• Писать без грамматических, орфографических и пунктуационных ошибок.

Этого делать не стоит:

• Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
• Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
• Использовать мат — это неуважительно по отношению к пользователям;
• Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Геометрия.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.

🌟 Видео

№262 В треугольниках ABC и А1В1С1 углы А и А1 — прямые, BD и В1D1— биссектрисы. Докажите, чтоСкачать

Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Признаки равенства треугольников. 7 класс.Скачать

Геометрия 7 класс (Урок№13 - Равнобедренный треугольник.)Скачать

№164. На сторонах равностороннего треугольника ABC отложены равные отрезки AD, BE и CF, как показаноСкачать

Задачи на доказательство по геометрии. Первый признак равенства треугольников.Скачать

Геометрия 7 класс (Урок№15 - Решение задач на признаки равенства треугольников.)Скачать

№110. Докажите, что если медиана треугольника совпадает с его высотой, то треугольникСкачать

Признаки равенства треугольников. Практическая часть. 7 класс.Скачать

7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать