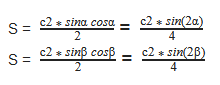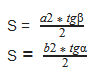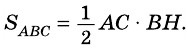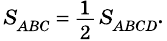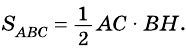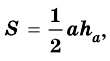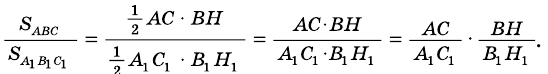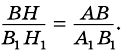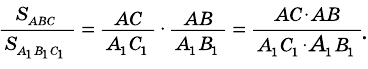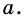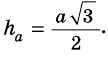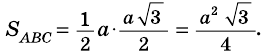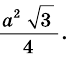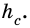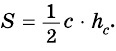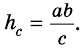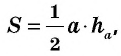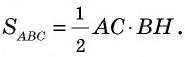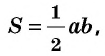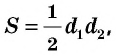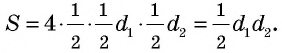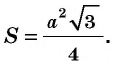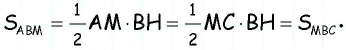Доказать площадь прямоугольного треугольника

О чем эта статья:

площадь, 8 класс

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Видео:Найдите площадь прямоугольного треугольника, если сумма его катетов равна 15, а гипотенуза равна 13Скачать

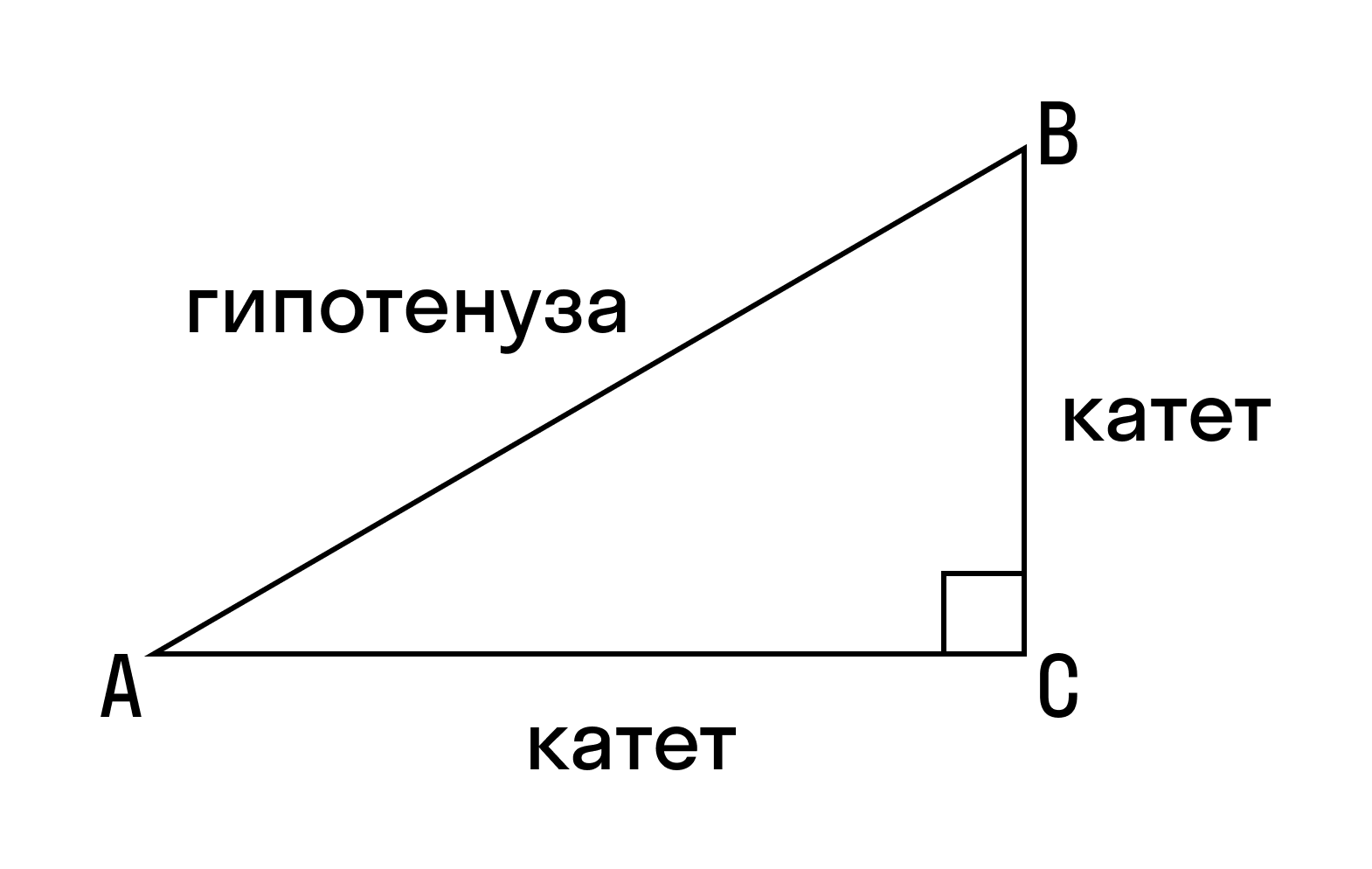
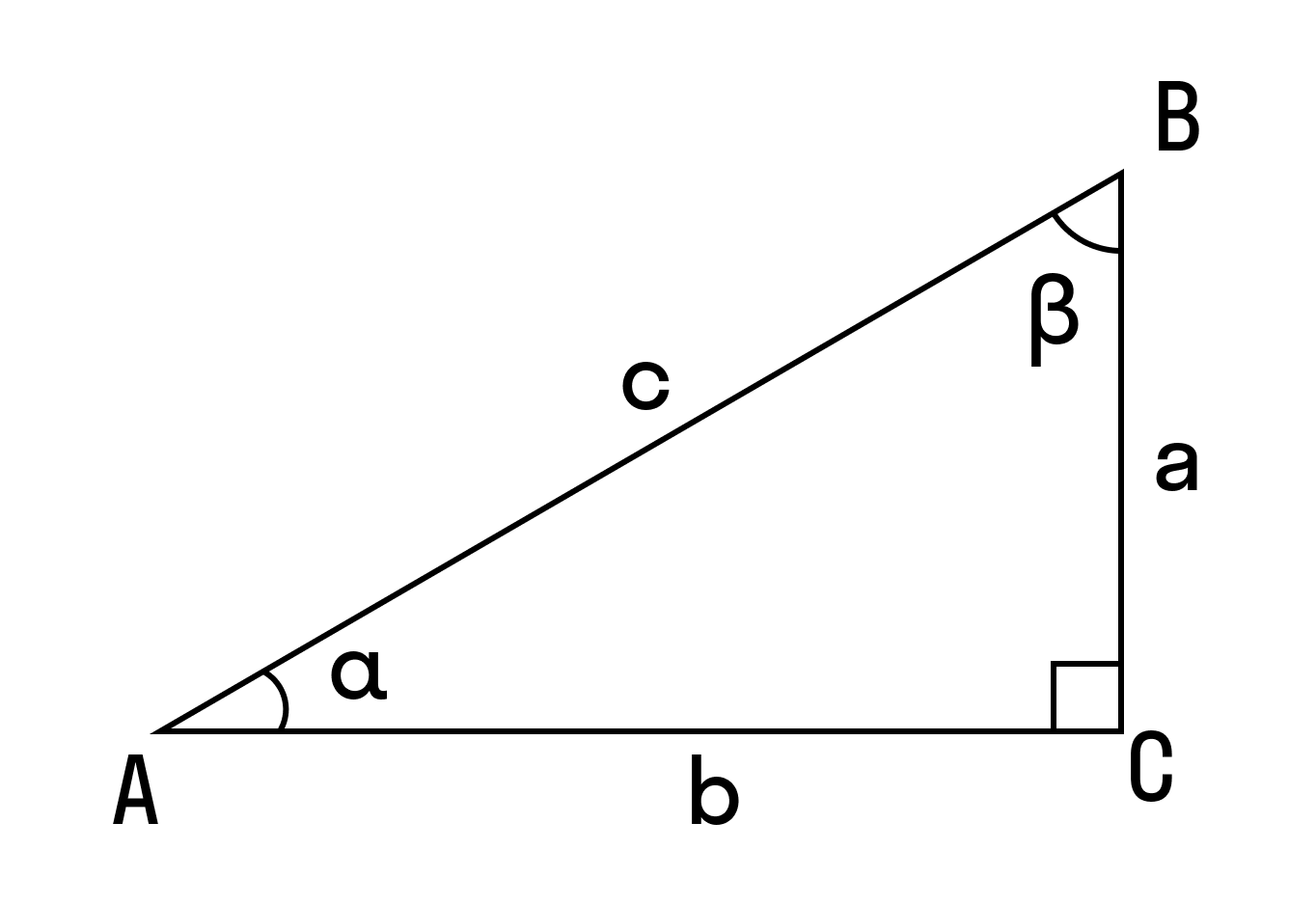
Основные определения

Прямоугольный треугольник — это треугольник, в котором один угол прямой, то есть равен 90˚.

Гипотенуза — это сторона, противолежащая прямому углу.

Катеты — это стороны, прилежащие к прямому углу.

Чтобы найти площадь прямоугольного треугольника, можно применить любую формулу нахождения площади треугольника — их несколько.

Видео:8 класс, 14 урок, Площадь треугольникаСкачать

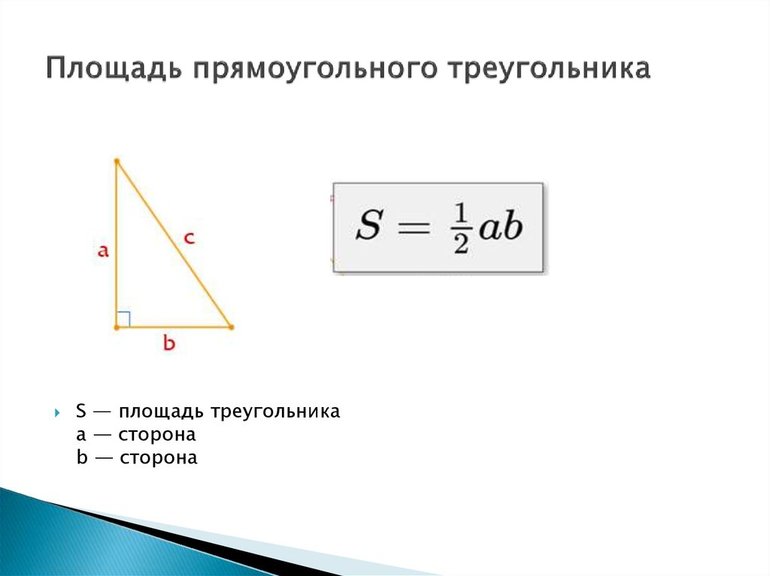
Формула для нахождения площади прямоугольного треугольника через катеты

Чтобы найти площадь, нужно вывести формулу:

Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию.

Так как в прямоугольном треугольнике катеты перпендикулярны, то один катет — это высота, проведенная ко второму катету.

Отсюда следует, что площадь прямоугольного треугольника равна половине произведения его катетов.

Используйте эту формулу, чтобы найти площадь прямоугольного треугольника через катеты.

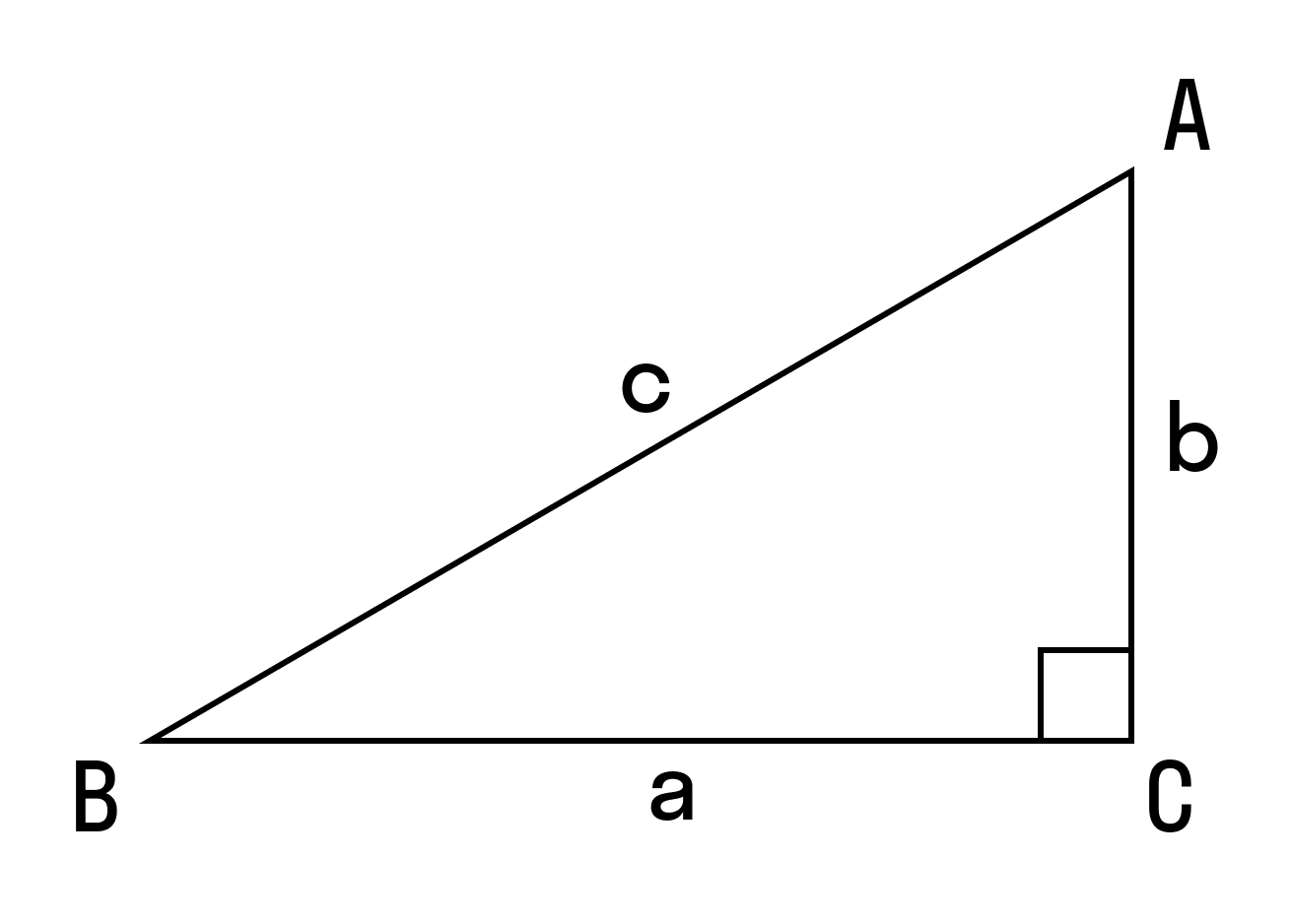
S = 1/2 (a × b), где a и b — катеты

Видео:Площадь прямоугольного треугольника. Как найти площадь прямоугольного треугольника?Скачать

Формула для нахождения площади прямоугольного треугольника через гипотенузу

Площадь прямоугольного треугольника равна половине произведения гипотенузы на высоту, проведенную к гипотенузе.

где с — гипотенуза,

Используйте эту формулу, чтобы найти площадь прямоугольного треугольника через гипотенузу.

Видео:9 класс, 12 урок, Теорема о площади треугольникаСкачать

Формула для нахождения площади прямоугольного треугольника через гипотенузу и острый угол

α, β — острые углы

Видео:Площадь прямоугольного треугольникаСкачать

Формулы нахождения площади прямоугольного треугольника через катет и угол

α, β — острые углы

Видео:Как находить площадь любой фигуры? Геометрия | МатематикаСкачать

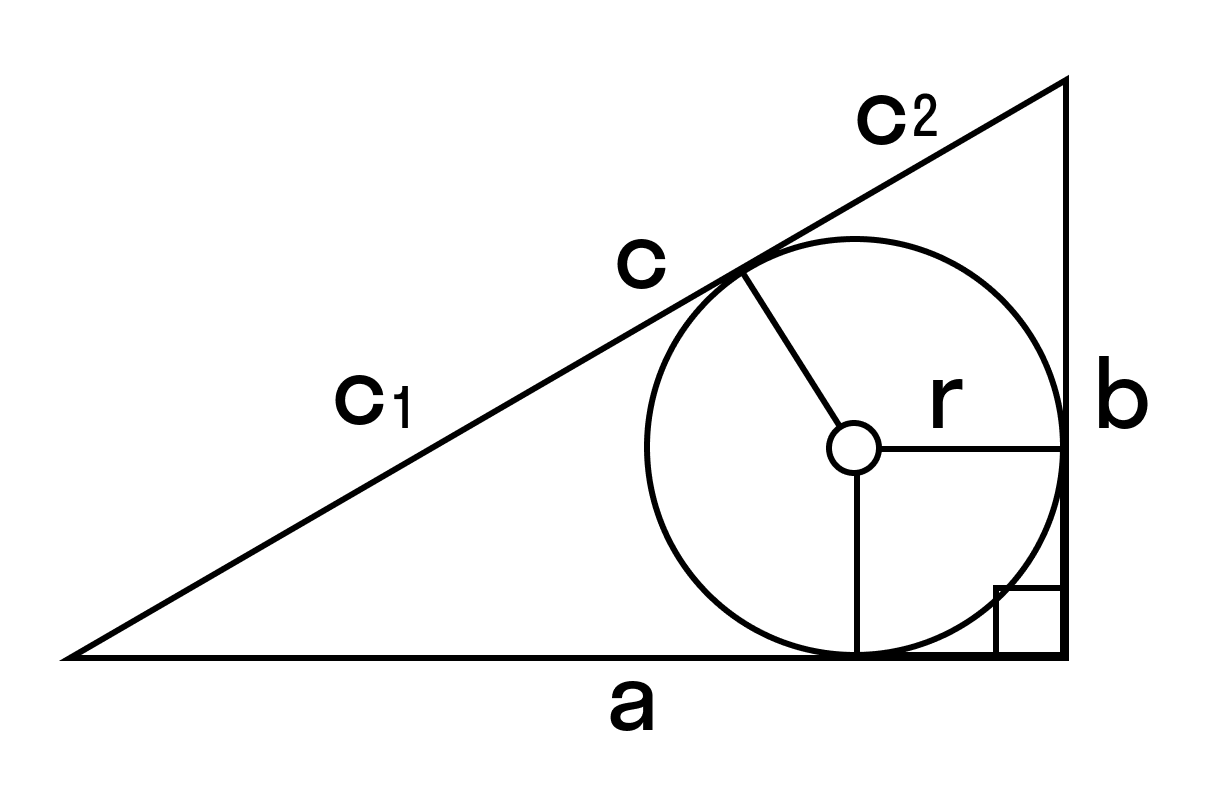
Формулы нахождения площади прямоугольного треугольника через радиус вписанной окружности и гипотенузу

Радиус вписанной окружности выражается через катеты и гипотенузу по формуле:

S прямоугольного треугольника = r (r + c) = c1 × c2

r — радиус вписанной окружности

C1 и С2 — отрезки, полученные делением гипотенузы на две части точкой касания с окружностью

Уверены, что во всем разобрались? Закрепите знания на курсах обучения математике в онлайн-школе Skysmart!

Видео:Геометрия 8 класс (Урок№10 - Площадь треугольника.)Скачать

Площадь прямоугольного треугольника через катеты — формула и примеры расчетов

Видео:Площадь треугольника. Как найти площадь треугольника?Скачать

Свойства треугольника

Пожалуй, в жизни любой человек сталкивается с треугольниками. Они бывают разными: остроугольными, тупоугольными, прямоугольными, равнобедренными и равносторонними. Но всех их объединяет один признак — существование трёх углов. Точное определение фигуре дали ещё в Древней Греции. Евклид утверждал, что этот объект состоит из трёх точек, расположенных на разных прямых, и трёх замкнутых линий, поочерёдно соединяющих эти точки.

Три точки, ограничивающие отрезки, называют вершинами, а линии, соединяющие их, — сторонами. Внутреннюю плоскость, заключённую в линии, называют площадью. Так как отрезки фигуры образуют три угла, то объект относится к классу многоугольников. Замкнутая прямая, соединяющая вершину с серединой противолежащей стороны, носит имя медиана. Всего их может быть три штуки, пересекаться они могут в одной точке, которую называют центроидом. Он является центром тяжести.

Если из угла провести перпендикуляр к противолежащей стороне, то полученная линия будет высотой. Линия, опущенная к стороне напротив угла и разделяющая его пополам, называется биссектрисой. В любой треугольник можно вписать окружность. Она будет единственной, так как должна касаться всех трёх сторон. Центр круга всегда будет совпадать с местом пересечения биссектрис.

Разделение треугольников происходит по размерам углов и сторон. Например, у равносторонней фигуры любой из трёх углов равен 60 градусам, у равнобедренной — две стороны и два угла равны. Для любого треугольника справедливо утверждать следующее:

• всегда напротив длинной стороны будет находиться больший угол;
• если две стороны равны, то напротив них будут равные углы;
• при сложении значений всех углов сумма составит 180 градусов;
• продолжив сторону за пределы объекта, можно получить внешний угол;
• одна из сторон всегда будет меньше суммы оставшихся и больше их разности.

В элементарной математике часто используют правила, называемые признаками подобия и равенства. Так, при сравнении две фигуры будут равными, если длины их сторон совпадают. Соответственно, углы тоже станут одинаковыми или будут равными две стороны и угол между ними.

Видео:Решение прямоугольных треугольников. Практическая часть. 8 класс.Скачать

Прямоугольная фигура

Треугольник с одним прямым углом, то есть составляющим 90 градусов, называется прямоугольным. Два отрезка, примыкающие к нему, называют катетами, а прямую, соединяющую их, — гипотенузой. Из любого треугольника можно получить две прямоугольных фигуры. Для этого нужно в нём опустить высоту. Многие свойства многоугольника идентичны прямоугольной фигуре. Два равных треугольника можно объединить в прямоугольник, при этом их гипотенузы будут совпадать с диагональю.

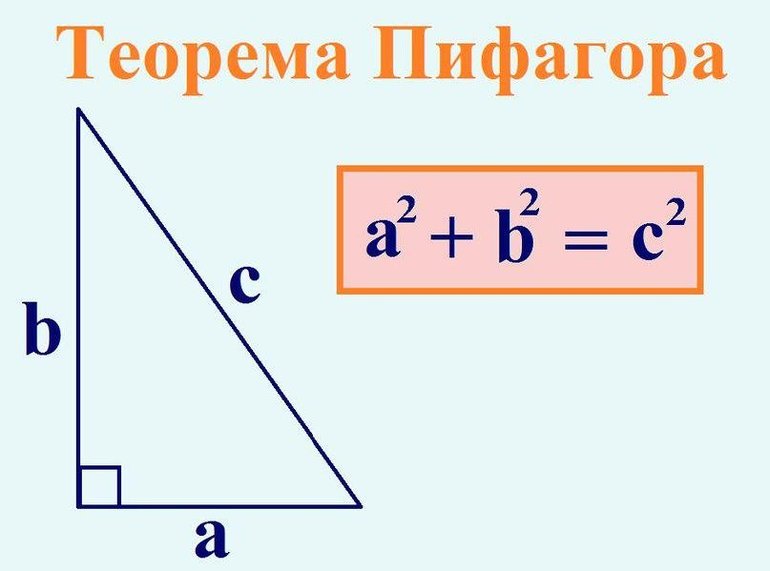
Основную особенность фигуры, которая позволяет посчитать площадь, подметил ещё Пифагор. Она очень простая и записывается как с 2 = а 2 + b 2 . В соответствии с этим правилом квадрат гипотенузы равняется результату сложения квадратов катетов, то есть сумма площадей квадратов, достроенных на катетах, совпадает с площадью квадрата, построенного на гипотенузе. Кроме основного свойства, чтобы найти площадь прямоугольного треугольника, нужно знать следующие правила:

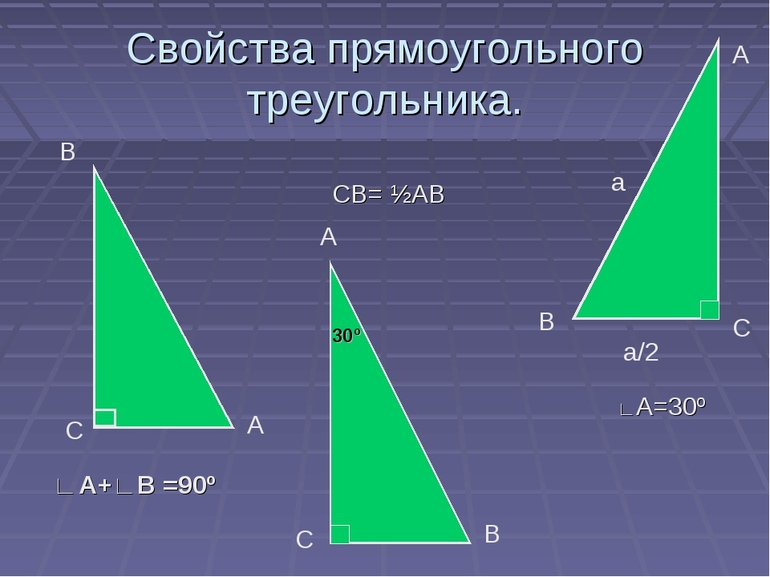
• при сложении двух острых углов сумма будет равняться 90 градусов;
• гипотенуза у фигуры всегда будет больше катета;
• длину катета, расположенного напротив угла в 30 градусов, можно найти, разделив гипотенузу пополам;
• катеты в прямоугольном треугольнике одновременно являются его высотами;
• величина радиуса описанной окружности совпадает с медианой.

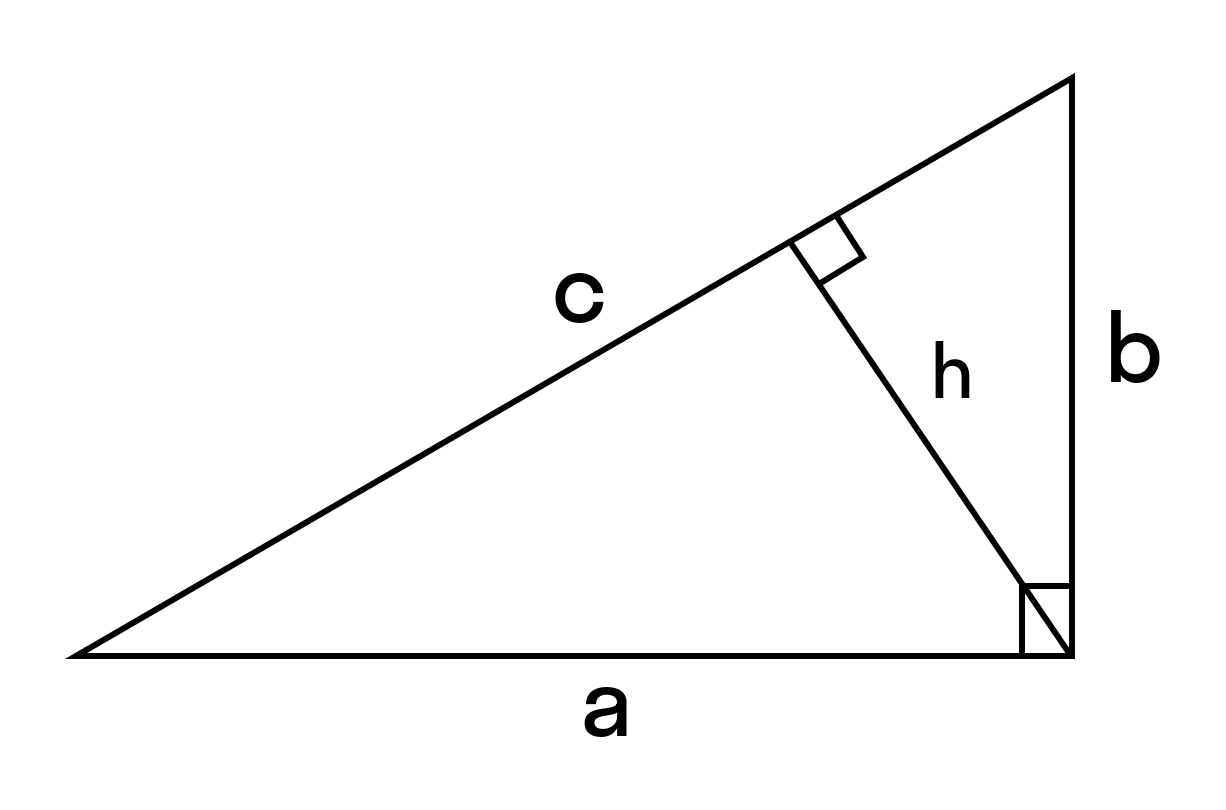
Из теоремы Пифагора можно сделать важное следствие. Становится очевидным, что высота, опущенная из прямого угла, разделит гипотенузу на два отрезка: c1 = a2/c и c1 = b2/c. Полученные замкнутые линии являются проекциями катетов. В то же время высоту фигуры можно определить, используя следующую формулу: h = √ca + cb.

Если угол, располагающийся напротив катета a, обозначить альфой, а напротив b — бетой, то справедливо утверждать, что гипотенуза будет равняться: c = b /sin b = a / sin a = b / cos a = a / cos b = h = √a 2 + b 2 . Другими словами, длины катетов можно вычислить, используя синус противолежащего угла или косинус прилежащего. То есть получатся равенства: a = c * sin a = c * cos b и b = c * cos a = c * sin b. Учитывая тригонометрические правила, катеты можно найти, используя тангенс. Так, сторона b = a * tg b, катет a = b * tg a.

Все рассмотренные формулы и свойства помогают при нахождении площади фигуры. Но кроме них полезно знать и то, что радиус вписанной окружности в прямоугольную фигуру можно узнать, найдя разницу суммы катетов и гипотенузы, разделённую на 2, то есть r = (a + b — c) / 2.

Видео:7 кл г. Теорема: «катет лежавший напротив угла в 30 градусов равен половине гипотенузы»Скачать

Формулы площади

Найти площадь треугольника с прямым углом можно различными способами. Но проще всего это сделать через катеты. Выражение для нахождения параметра довольно простое: S = (a * b) / 2. Это классическая формула площади прямоугольного треугольника. Существуют и другие формулы:

• S = (a 2 * tg b) / 2;
• S = (a 2 * ctg a) / 2;
• S = (b 2 * tg a) / 2;
• S = (b 2 * ctg b) / 2.

Другими словами, площадь можно определить, зная значения двух катетов, длину одного из них и разворот противолежащего или прилежащего угла. Для доказательства теоремы нахождения площади понадобится изобразить фигуры с катетами b и a. Фигуру можно достроить до параллелограмма, отложив параллельные катетам прямые. Вершины полученного объекта можно обозначить буквами A, B, C, D, начиная с прямого угла треугольника и двигаясь влево.

Прямоугольник образуется двумя треугольниками, равными между собой по трём сторонам: AB = CD, AC = BD (ВС — общая сторона). Учитывая равенства, можно утверждать, что площади фигур равны друг другу. Следовательно, площадь параллелограмма можно найти через сумму площадей двух треугольников: S = Sabc + Sacd. Отсюда верным будет утверждение, что площадь начального треугольника ABC равняется половине замкнутой области прямоугольника, а та соответствует произведению сторон: S = a * b, то есть AB * BC.

Эта формула легко доказывается с учётом того, что прямоугольник является фигурой, в которую можно вписать несколько четырёхугольников. Так как общая площадь будет равняться сумме площадей внутренних фигур, то верным будет равенство: (a + b)2 = S + S + a2 + b2 = a2 + 2ab + b2 = 2S + a2 + b2. Отсюда получим, что S = a* b. Следовательно, так как площадь треугольника равняется половине площади прямоугольной фигуры, то можно утверждать, что S = (a * b)/2 = (AB * BC) / 2. Формула доказана.

Из этого правила вытекают два следствия:

• площадь равняется половине результата перемножения катетов;
• когда высоты двух треугольных фигур совпадают, их площади можно соотнести как основания.
• если угол одного треугольника равен углу другого, то площади объектов соотносятся как результат умножения сторон с одинаковыми углами.

Использование рассмотренных следствий помогает при решении многих геометрических задач. Они касаются не только треугольников, но и других многоугольных фигур.

Видео:Урок 38. Площадь треугольника, прямоугольного треугольника, ромбаСкачать

Решение задач

Важно не только знать формулы для нахождения площади, но и уметь их применять на практике. Это возможно лишь с опытом, который можно получить, решая различные задания. Существуют определённые задачи, которые ученикам нужно решить самостоятельно. После успешного решения можно утверждать, что учащиеся полностью разобрались в теме, поэтому они могут переходить к следующему разделу геометрии. Вот некоторые задания, позволяющие закрепить теоретический материал:

1. В прямоугольнике одна из сторон равна 35 см, а другая — 50 см. Нужно найти площадь фигур, полученных в результате проведения диагонали. В соответствии с правилом диагональ прямоугольника разделяет его на два равных прямоугольных треугольника, при этом его стороны являются катетами полученных фигур. Отсюда следует, что S1 = S2 = a * b / 2 = 35 * 50 / 2 = 1750 / 2 = 875 см².
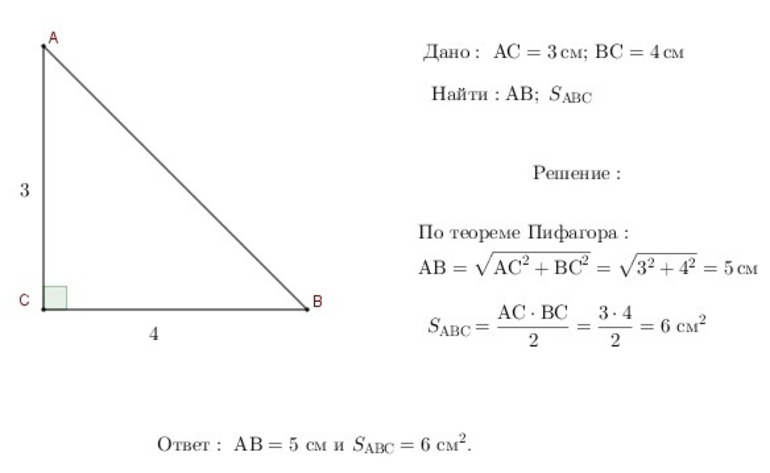
2. Есть прямоугольный треугольник, катет которого равняется 15 см, а гипотенуза — 25 см. Нужно вычислить площадь фигуры. Для решения задачи следует узнать длину второго катета. Сделать это удастся, используя формулу гипотенузы: c = √a2 + b2. Из неё можно выразить неизвестный катет. Его длина будет равняться: b = √c2 — a2 = √252 — 152 = √625 — 225 = √400 = 20 см. Известные данные нужно подставить в формулу площади и выполнить расчёт: S = 20 * 15 / 2 = 150 см².

Длина катета в треугольнике равна 2 * √3 см, а противолежащий ему угол составляет 50 градусов. Необходимо вычислить площадь фигуры. Известно, что сумма углов в таком треугольнике — 180 градусов. Следовательно, разворот прилежащего к катету углу равняется a = 180 — 90 — b = 180 — 90 — 60 = 30 градусов. Теперь можно использовать формулу для нахождения площади прямоугольного многоугольника через катет и тангенс угла: S = (b 2 * tg a) / 2 = ((2 * √3) 2 * tg 30) / 2 = (12/2) * (√3/3) = 2√3 см 2 .

Таким образом, площадь прямоугольной фигуры — ее численная характеристика. Определить ее можно, используя несколько способов. При этом всегда необходимо знать длину хотя бы одного из катетов. Это связанно с тем, что две из трёх высот совпадают с ним.

Видео:Геометрия 9 класс (Урок№14 - Теорема о площади треугольника.)Скачать

Площадь треугольника — определение и вычисление с примерами решения

Площадь треугольника:

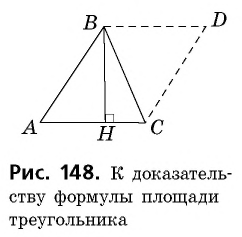
Теорема (о площади треугольника). Площадь треугольника равна половине произведения его стороны на высоту, к ней проведенную.

Доказательство:

Пусть

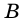
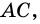
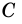
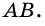
1) Проведем через вершину прямую, параллельную а через вершину — прямую, параллельную Получим параллелограмм

2) (по трем сторонам). Поэтому

откуда

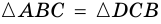
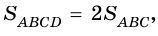
3) Так как 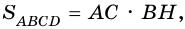то

В общем виде формулу площади 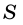треугольника можно записать так:

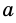
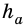
где — сторона треугольника, — высота, проведенная к ней.

Следствие 1. Площадь прямоугольного треугольника равна половине произведения катетов.

Следствие 2. Если сторона одного треугольника равна стороне другого треугольника, то площади таких треугольников относятся как их высоты, проведенные к этим сторонам.

Следствие 3. Если высота одного треугольника равна высоте другого треугольника, то площади этих треугольников относятся как стороны, к которым проведены эти высоты.

Пример:

Докажите, что если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, образующих этот угол.

Доказательство:

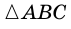
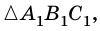
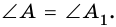
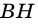
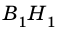
Рассмотрим и у которых Проведем высоты и (рис. 238).

2) (по острому углу), поэтому

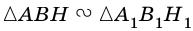
3) Имеем:

Пример:

Найдите площадь равностороннего треугольника, сторона которого равна

Решение:

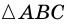
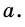
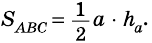
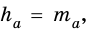
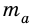
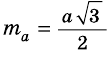
Пусть — равносторонний со стороной Тогда В равностороннем треугольнике где — медиана. Но (§ 18, задача 4), поэтому

Следовательно,

Ответ.

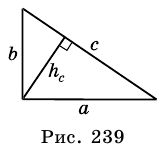
Пример:

Стороны треугольника равны 8 см, 15 см и ^ 17 см. Найдите высоту треугольника, проведенную к его наибольшей стороне.

Решение:

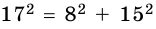
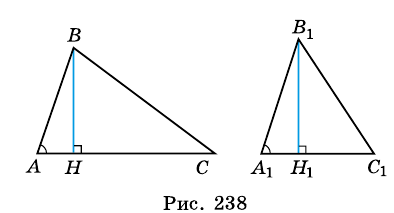
Так как (т. е. 289 = 289), то по теореме, обратной теореме Пифагора, треугольник является прямоугольным. Прямой угол является противолежащим к стороне, равной 17 см.

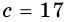
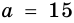
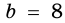
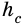
Пусть на рис. 239 изображен прямоугольный треугольник, у которого см -гипотенуза, и см — катеты, — высота. Найдем

Площадь этого треугольника можно найти

по формулам: 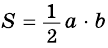или

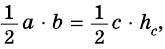
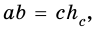
Тогда то есть откуда

Таким образом, имеем: 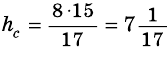(см).

Ответ. 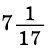см.

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Теорема (формула площади треугольника)

Площадь треугольника равна половине произведения его стороны на высоту, проведенную к этой стороне:

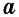
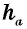
где — сторона треугольника, — проведенная к ней высота.

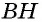
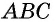
Пусть — высота треугольника (рис. 148). Докажем, что

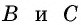
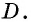
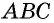
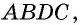
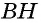
Проведем через вершины прямые, параллельные сторонам треугольника, и обозначим точку их пересечения Таким образом, мы «достроили» треугольник до параллелограмма в котором отрезок также является высотой, проведенной к стороне

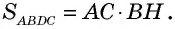
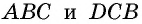
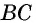
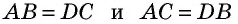
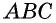
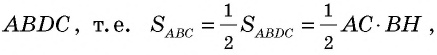
По формуле площади параллелограмма Треугольники равны по трем сторонам (у них сторона общая, как противолежащие стороны параллелограмма). Эти треугольники имеют равные площади. Тогда площадь треугольника составляет половину площади параллелограмма что и требовалось доказать.

Следствие 1

Площадь прямоугольного треугольника равна половине произведения его катетов:

где 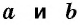— катеты прямоугольного треугольника.

Действительно, в прямоугольном треугольнике высота, проведенная к катету, совпадает с другим катетом.

Следствие 2

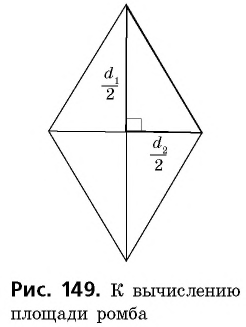
Площадь ромба равна половине произведения его диагоналей:

где 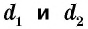— диагонали ромба.

Действительно, диагонали делят ромб на четыре равных прямоугольных треугольника с катетами 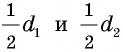(рис. 149). Используя следствие 1, имеем:

Следствие 3

Площадь равностороннего треугольника со стороной 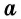вычисляется по формуле

Обоснуйте это следствие самостоятельно.

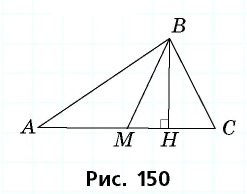
Опорная задача

Медиана делит треугольник на два равновеликих треугольника. Докажите.

Решение:

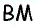
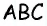
Пусть — медиана треугольника (рис. 150).

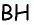
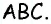
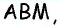
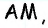
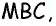
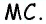
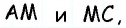
Проведем высоту треугольника Этот отрезок является одновременно высотой треугольника проведенной к стороне и высотой треугольника проведенной к стороне Учитывая равенство отрезков имеем:

Эта задача имеет интересные обобщения: если высоты двух треугольников равны, то отношение площадей этих треугольников равно отношению их оснований; если основания двух треугольников равны, то отношение площадей этих треугольников равно отношению их высот.

Докажите эти утверждения самостоятельно.

• Соотношения между сторонами и углами произвольного треугольника
• Окружность и круг
• Описанные и вписанные окружности
• Плоские и пространственные фигуры
• Взаимное расположения прямых на плоскости
• Треугольник
• Решение треугольников
• Треугольники и окружность

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

📸 Видео

Площадь прямоугольного треугольника равна 200√3 ... | ОГЭ 2017 | ЗАДАНИЕ 9 | ШКОЛА ПИФАГОРАСкачать

№471. Найдите площадь прямоугольного треугольника, если его катеты равны: а) 4 см и 11см;Скачать

Найдите площадь прямоугольного треугольника ... | ОГЭ 2017 | ЗАДАНИЕ 9 | ШКОЛА ПИФАГОРАСкачать

КАТЕТЫ И ВЫСОТА В ПРЯМОУГОЛЬНОМ ТРЕУГОЛЬНИКЕ ЧАСТЬ I #математика #егэ #огэ #Shorts #геометрияСкачать

4 класс, 25 урок, Площадь прямоугольного треугольникаСкачать

Высота в прямоугольном треугольнике. 8 класс.Скачать

КАК НАЙТИ ПЛОЩАДЬ ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА? Примеры | МАТЕМАТИКА 5 классСкачать