Диаметры окружности пересекаются под углом 60

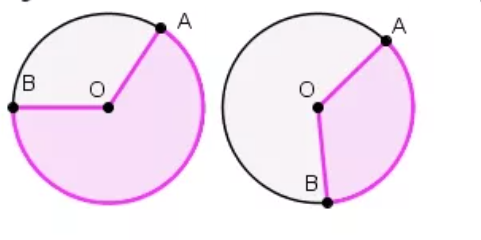
Найти длины хорд АД и ДС, Найти радиус окружности. Помогите пожалуйста.

это не школьники такие, а учителя, которые составляют задачи .

если дуга окружности в секторе 60град равна 4п, то длина всей окружности (360град) S = 4п х 360/60 = 4п х 6 = 24п см

длина окружности (формулу надо запомнить один раз на всю жизнь) S = 2пR (читается двапиэр) , стало быть, радиус R = S / 2п
раеньше мы уже посчитали, что S = 24п см, стало быть
R = 24п / 2п = 12 см

В условиях явно какая-то фигня. Наверно, девушка радиус с диаметром спутала.
«Диаметры АС и АД пересекаются. »
пересекаются они в точке А — т. к. она, судя по названию отрезков (АС и АД) , общая. Но диаметры одной и той же окружности могут пересекаться только в своей середине — а точка А — это конец отрезка, а не середина! Фиг поймешь этих школьников.

Короче, длина хорды в секторе 60 градусов будет равна радиусу — т. е. 12 см.
Почему? потому что имеем треугольник, у которого две стороны — радиусы, а третья сторона — хорда. Треугольник — равнобедренный (т. к. две стороны — одинаковые — радиусы) , хорда — это его основание. В равнобедренном треугольнике углы при основании равны. Сумма углов треугольника — 180 град (это надо запомнить на всю жизнь) , угол при вершине 60 град, стало быть, углы при основании в сумме составляют 180-60=120 град, т. е. каждый угол в отдельности 60 град, т. е. все углы равны 60 град — это равносторонний треугольник! Стало быть, третья сторона (хорда) такая же, как боковые стороны (радиусы) — 12 см
Это мы нашли короткую хорду — там есть еще длинная.. .
Там можно по теореме Пифагора.. . можно по синусам косинусам.. .
Короче, длинная хорда будет 2Rcos30град= 2 х 12 х корень из 3 пополам = 12 корней из трех см.
(и короткую хорду можно было через синусы-косинусы = 2Rsin30град = 2 х 12 х 1/2 = 12см)

Диаметры окружности пересекаются под углом

В окружности диаметры ac и bd пересекаются под углом 60 градусов?

Геометрия | 10 — 11 классы

В окружности диаметры ac и bd пересекаются под углом 60 градусов.

Найдите сторону cd четырёхугольника abcd, если радиус окружности 6см.

Пусть ас и bd пересекаются в k, тогда угол dkc = 60 градусам ; мы знаем что

диаметр равен двум радиусам, поэтому dk = kc = 6,

отсюда следует что треугольник dkc – равнобедренный, тогда углы kdc и kcd — равны (180 — 60) : 2 = 60

градусов, значит треугольник dkc –равносторонний, тогда dc = 6.

В ромбе ABCD диагонали пересекаются в точке о?

В ромбе ABCD диагонали пересекаются в точке о.

В ромб вписана окружность, касающаяся стороны AD в точке Е.

Найти отношение диаметра окружности к стороне ромба, если кут OAE = 75 градусов.

Вершины четырёхугольника ABCD лежат на окружности, а его диагонали являются диаметрами этой окружности?

Вершины четырёхугольника ABCD лежат на окружности, а его диагонали являются диаметрами этой окружности.

Сторона AB = 3 см, чему равна противолежащая ей сторона?

Окружность, длина радиуса которой равна 2 см, касается всех сторон четырёхугольника ABCD?

Окружность, длина радиуса которой равна 2 см, касается всех сторон четырёхугольника ABCD.

Известно , что точки касания являются серединами сторон четырёхугольника.

Вычислите периметр четырёхугольника ABCD.

Четырёхугольник ABCD со сторонами AB = 11 и CD = 41 вписан в окружность?

Четырёхугольник ABCD со сторонами AB = 11 и CD = 41 вписан в окружность.

Диагонали AC и BD пересекаются в точке K , причём ∠AKB = 60∘ .

Найдите радиус окружности, описанной около этого четырёхугольника.

Помогите?

В четырёхугольник ABCD со сторонами AB = 19 и CD = 28 вписан в окружность.

Диагонали AC и BD пересекаются в точке K , причём ∠AKB = 60∘ .

Найдите радиус окружности, описанной около этого четырёхугольника.

Четырёхугольник ABCD со сторонами AB = 34 и CD = 22 вписан в окружность?

Четырёхугольник ABCD со сторонами AB = 34 и CD = 22 вписан в окружность.

Диагонали AC и BD пересекаются в точке K , причём ∠AKB = 60° Найдите радиус окружности, описанной около этого четырёхугольника.

Четырёхугольник ABCD со сторонами AB = 3 и CD = 5 вписан в окружность?

Четырёхугольник ABCD со сторонами AB = 3 и CD = 5 вписан в окружность.

Диагонали AC и BD пересекаются в точке K, причём угол AKB = 60.

Найдите радиус окружности, описанной около этого четырёхугольника.

Трапеция ABCD с основаниями AD и BC вписана в окружность с диаметром AD?

Трапеция ABCD с основаниями AD и BC вписана в окружность с диаметром AD.

Найти углы трапеции, если ее диагонали пересекаются под углом 40 градусов.

О — центр окружности, AB — диаметр, СD — хорда?

О — центр окружности, AB — диаметр, СD — хорда.

Диаметр пересекается с хордой под углом 90 градусов в точке E.

Радиус окружности равен 6 см, угол = 60 градусов.

Найдите ED ; OCD, угол OCD(желательно с чертежом).

Четырёхугольник ABCD вписан в окружность?

Четырёхугольник ABCD вписан в окружность.

Угол C меньше угла A на 140 градусов и в 3 раза меньше угла B.

Найдите углы четырёхугольника.

Вы зашли на страницу вопроса В окружности диаметры ac и bd пересекаются под углом 60 градусов?, который относится к категории Геометрия. По уровню сложности вопрос соответствует учебной программе для учащихся 10 — 11 классов. В этой же категории вы найдете ответ и на другие, похожие вопросы по теме, найти который можно с помощью автоматической системы «умный поиск». Интересную информацию можно найти в комментариях-ответах пользователей, с которыми есть обратная связь для обсуждения темы. Если предложенные варианты ответов не удовлетворяют, создайте свой вариант запроса в верхней строке.

4 дня ждал, когда кто — нибудь, кому нужны баллы решит эту задачу. Терпелка лопнула. Привожу в двух приложениях два способа решения этой задачи.

Отрезки и прямые, связанные с окружностью. Теорема о бабочке

Отрезки и прямые, связанные с окружностью

Свойства хорд и дуг окружности

Теоремы о длинах хорд, касательных и секущих

Доказательства теорем о длинах хорд, касательных и секущих

Теорема о бабочке

Отрезки и прямые, связанные с окружностью

Фигура	Рисунок	Определение и свойства
Окружность

Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности

Круг

Конечная часть плоскости, ограниченная окружностью

Радиус

Отрезок, соединяющий центр окружности с любой точкой окружности

Хорда

Отрезок, соединяющий две любые точки окружности

Диаметр

Хорда, проходящая через центр окружности.

Диаметр является самой длинной хордой окружности

Касательная

Прямая, имеющая с окружностью только одну общую точку.

Касательная перпендикулярна к радиусу окружности, проведённому в точку касания

Секущая

Прямая, пересекающая окружность в двух точках

Окружность

Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности

Круг

Конечная часть плоскости, ограниченная окружностью

Радиус

Отрезок, соединяющий центр окружности с любой точкой окружности

Хорда

Отрезок, соединяющий две любые точки окружности

Диаметр

Хорда, проходящая через центр окружности.

Диаметр является самой длинной хордой окружности

Касательная

Прямая, имеющая с окружностью только одну общую точку.

Касательная перпендикулярна к радиусу окружности, проведённому в точку касания

Секущая

Прямая, пересекающая окружность в двух точках

Свойства хорд и дуг окружности

Фигура	Рисунок	Свойство
Диаметр, перпендикулярный к хорде		Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам.
Диаметр, проходящий через середину хорды		Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам.
Равные хорды		Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности.
Хорды, равноудалённые от центра окружности		Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны.
Две хорды разной длины		Большая из двух хорд расположена ближе к центру окружности.
Равные дуги		У равных дуг равны и хорды.
Параллельные хорды		Дуги, заключённые между параллельными хордами, равны.

Диаметр, перпендикулярный к хорде

Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам.

Диаметр, проходящий через середину хорды

Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам.

Равные хорды

Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности.

Хорды, равноудалённые от центра окружности

Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны.

Две хорды разной длины

Большая из двух хорд расположена ближе к центру окружности.

Равные дуги

У равных дуг равны и хорды.

Параллельные хорды

Дуги, заключённые между параллельными хордами, равны.

Теоремы о длинах хорд, касательных и секущих

Фигура	Рисунок	Теорема
Пересекающиеся хорды

Произведения длин отрезков, на которые разбита каждая из хорд, равны:

Касательные, проведённые к окружности из одной точки

Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.

Касательная и секущая, проведённые к окружности из одной точки

Секущие, проведённые из одной точки вне круга

Произведения длин отрезков, на которые разбита каждая из хорд, равны:

Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.

Пересекающиеся хорды

Касательные, проведённые к окружности из одной точки

Касательная и секущая, проведённые к окружности из одной точки

Секущие, проведённые из одной точки вне круга

Пересекающиеся хорды

Произведения длин отрезков, на которые разбита каждая из хорд, равны:

Касательные, проведённые к окружности из одной точки

Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.

Касательная и секущая, проведённые к окружности из одной точки

Секущие, проведённые из одной точки вне круга

Доказательства теорем о длинах хорд, касательных и секущих

Теорема 1 . Предположим, что хорды окружности AB и CD пересекаются в точке E (рис.1).

Тогда справедливо равенство

Доказательство . Заметим, что углы BCD и BAD равны как вписанные углы, опирающиеся на одну и ту же дугу. Углы BEC и AED равны как вертикальные. Поэтому треугольники BEC и AED подобны. Следовательно, справедливо равенство

откуда и вытекает требуемое утверждение.

Теорема 2 . Предположим, что из точки A , лежащей вне круга, к окружности проведены касательная AB и секущая AD (рис.2).

Точка B – точка касания с окружностью, точка C – вторая точка пересечения прямой AD с окружностью. Тогда справедливо равенство

Доказательство . Заметим, что угол ABC образован касательной AB и хордой BC , проходящей через точку касания B . Поэтому величина угла ABC равна половине угловой величины дуги BC . Поскольку угол BDC является вписанным углом, то величина угла BDC также равна половине угловой величины дуги BC . Следовательно, треугольники ABC и ABD подобны (угол A является общим, углы ABC и BDA равны). Поэтому справедливо равенство

откуда и вытекает требуемое утверждение.

Теорема 3 . Предположим, что из точки A , лежащей вне круга, к окружности проведены секущие AD и AF (рис.3).

Точки C и E – вторые точки пересечения секущих с окружностью. Тогда справедливо равенство

Доказательство . Проведём из точки A касательную AB к окружности (рис. 4).

Точка B – точка касания. В силу теоремы 2 справедливы равенства

откуда и вытекает требуемое утверждение.

Теорема о бабочке

Теорема о бабочке . Через середину G хорды EF некоторой окружности проведены две произвольные хорды AB и CD этой окружности. Точки K и L – точки пересечения хорд AC и BD с хордой EF соответственно (рис.5). Тогда отрезки GK и GL равны.

Доказательство . Существует много доказательств этой теоремы. Изложим доказательство, основанное на теореме синусов, которое, на наш взгляд, является наиболее наглядным. Для этого заметим сначала, что вписанные углы A и D равны, поскольку опираются на одну и ту же дугу. По той же причине равны и вписанные углы C и B . Теперь введём следующие обозначения:

Воспользовавшись теоремой синусов, применённой к треугольнику CKG , получим

Воспользовавшись теоремой синусов, применённой к треугольнику AKG , получим

Воспользовавшись теоремой 1, получим

Воспользовавшись равенствами (1) и (2), получим

Проводя совершенно аналогичные рассуждения для треугольников BGL и DGL , получим равенство

откуда вытекает равенство

что и завершает доказательство теоремы о бабочке.

Окружность и круг

теория по математике 📈 планиметрия

Определения

Окружность – множество всех точек плоскости, равноудаленных от одной данной точки (центра окружности). Другими словами – это замкнутая линия, длину которой можно измерить.

На рисунке центр окружности обозначен точкой О. Определения

Радиус – расстояние от центра до любой точки окружности. На рисунке радиус обозначен АО. Все радиусы одной окружности равны. Радиус можно обозначать латинскими буквами R или r.

Диаметр – отрезок, который соединяет две точки окружности и проходит через её центр. На рисунке диаметр обозначен АВ. Все диаметры одной окружности равны. В одном диаметре содержится два радиуса. Диаметр обозначается буквой d.

Хорда – отрезок, соединяющий две любые точки окружности. На рисунке это отрезок CD.

Свойство хорд

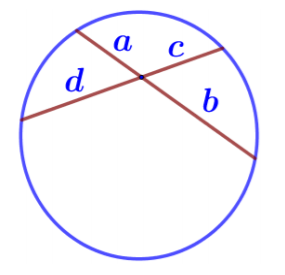
Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды. Так, на рисунке показаны две пересекающиеся хорды, одна состоит из отрезков a и b, вторая из отрезков d и с, следовательно, ab=dс.

Длина окружности

Длину окружности можно вычислить по формуле:

C=2πR, где π=3,14.

Дуга – часть окружности, которая соединяет две точки. На рисунке мы видим несколько дуг, например, дуги CD (малая и большая). Дуга АВ – называется полуокружностью, так как стягивает концы диаметра. Обозначается дуга значком ∪АВ.

Дуга, касательная, круг, сектор, сегмент

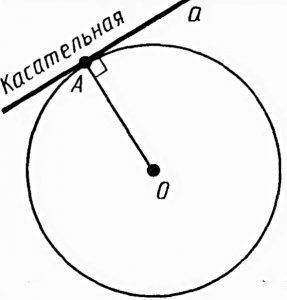
Из точки, не лежащей на окружности можно провести касательную – прямую, которая имеет с окружностью только одну общую точку (рисунок 4).

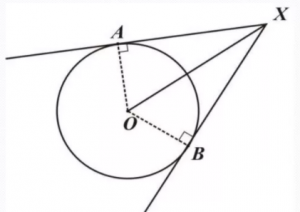
Свойства касательной

На рисунке видно, что АХ=ВХ, угол АХО равен углу ВХО.

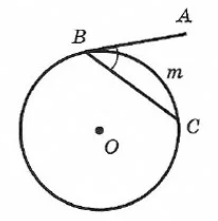
Угол АВС (образован касательной АВ и хордой ВС) равен половине дуги m.

Круг – часть плоскости, ограниченная окружностью. Другими словами, круг – это всё, что находится внутри окружности.

Площадь круга вычисляется по формуле:

S=πR 2 , где π=3,14.

Сектор и его площадь

Сектор – область круга, ограниченная двумя радиусами. На рисунке сектор выделен сиреневым цветом, он ограничен радиусами ОА и ОВ.

Площадь кругового сектора вычисляется по формуле:

S= π R 2 360 . . × α , где α – угол между радиусами.

Сегмент – это область круга, ограниченная хордой и дугой. На рисунке сегмент выделен сиреневым цветом. Также можно сказать, что это часть круга, отсекаемая от него хордой. На рисунке видно, как хорда АВ отсекает сегмент.

В окружности диаметры ac и bd пересекаются под углом 60 градусов?

Геометрия | 10 — 11 классы

В окружности диаметры ac и bd пересекаются под углом 60 градусов.

Найдите сторону cd четырёхугольника abcd, если радиус окружности 6см.

Пусть ас и bd пересекаются в k, тогда угол dkc = 60 градусам ; мы знаем что

диаметр равен двум радиусам, поэтому dk = kc = 6,

отсюда следует что треугольник dkc – равнобедренный, тогда углы kdc и kcd — равны (180 — 60) : 2 = 60

градусов, значит треугольник dkc –равносторонний, тогда dc = 6.

В ромбе ABCD диагонали пересекаются в точке о?

В ромбе ABCD диагонали пересекаются в точке о.

В ромб вписана окружность, касающаяся стороны AD в точке Е.

Найти отношение диаметра окружности к стороне ромба, если кут OAE = 75 градусов.

Вершины четырёхугольника ABCD лежат на окружности, а его диагонали являются диаметрами этой окружности?

Вершины четырёхугольника ABCD лежат на окружности, а его диагонали являются диаметрами этой окружности.

Сторона AB = 3 см, чему равна противолежащая ей сторона?

Окружность, длина радиуса которой равна 2 см, касается всех сторон четырёхугольника ABCD?

Окружность, длина радиуса которой равна 2 см, касается всех сторон четырёхугольника ABCD.

Известно , что точки касания являются серединами сторон четырёхугольника.

Вычислите периметр четырёхугольника ABCD.

Четырёхугольник ABCD со сторонами AB = 11 и CD = 41 вписан в окружность?

Четырёхугольник ABCD со сторонами AB = 11 и CD = 41 вписан в окружность.

Диагонали AC и BD пересекаются в точке K , причём ∠AKB = 60∘ .

Найдите радиус окружности, описанной около этого четырёхугольника.

Помогите?

В четырёхугольник ABCD со сторонами AB = 19 и CD = 28 вписан в окружность.

Диагонали AC и BD пересекаются в точке K , причём ∠AKB = 60∘ .

Найдите радиус окружности, описанной около этого четырёхугольника.

Четырёхугольник ABCD со сторонами AB = 34 и CD = 22 вписан в окружность?

Четырёхугольник ABCD со сторонами AB = 34 и CD = 22 вписан в окружность.

Диагонали AC и BD пересекаются в точке K , причём ∠AKB = 60° Найдите радиус окружности, описанной около этого четырёхугольника.

Четырёхугольник ABCD со сторонами AB = 3 и CD = 5 вписан в окружность?

Четырёхугольник ABCD со сторонами AB = 3 и CD = 5 вписан в окружность.

Диагонали AC и BD пересекаются в точке K, причём угол AKB = 60.

Найдите радиус окружности, описанной около этого четырёхугольника.

Трапеция ABCD с основаниями AD и BC вписана в окружность с диаметром AD?

Трапеция ABCD с основаниями AD и BC вписана в окружность с диаметром AD.

Найти углы трапеции, если ее диагонали пересекаются под углом 40 градусов.

О — центр окружности, AB — диаметр, СD — хорда?

О — центр окружности, AB — диаметр, СD — хорда.

Диаметр пересекается с хордой под углом 90 градусов в точке E.

Радиус окружности равен 6 см, угол = 60 градусов.

Найдите ED ; OCD, угол OCD(желательно с чертежом).

Четырёхугольник ABCD вписан в окружность?

Четырёхугольник ABCD вписан в окружность.

Угол C меньше угла A на 140 градусов и в 3 раза меньше угла B.

Найдите углы четырёхугольника.

Вы зашли на страницу вопроса В окружности диаметры ac и bd пересекаются под углом 60 градусов?, который относится к категории Геометрия. По уровню сложности вопрос соответствует учебной программе для учащихся 10 — 11 классов. В этой же категории вы найдете ответ и на другие, похожие вопросы по теме, найти который можно с помощью автоматической системы «умный поиск». Интересную информацию можно найти в комментариях-ответах пользователей, с которыми есть обратная связь для обсуждения темы. Если предложенные варианты ответов не удовлетворяют, создайте свой вариант запроса в верхней строке.