Видео:Радиус перпендикулярный хорде делит ее пополамСкачать

Ваш ответ
Видео:Теорема о диаметре, перпендикулярном хордеСкачать

решение вопроса
Видео:Геометрия 8 класс (Урок№28 - Свойства хорд окружности.)Скачать

Похожие вопросы
- Все категории
- экономические 43,282
- гуманитарные 33,619
- юридические 17,900
- школьный раздел 607,049
- разное 16,829
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Диаметр окружности перпендикулярен хорде делит эту хорду пополам доказательство
ОКРУЖНОСТЬ И КРУГ. ЦИЛИНДР.
§ 70. ДИАМЕТР, ПЕРПЕНДИКУЛЯРНЫЙ К ХОРДЕ.
Теорема 1. Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею дуги пополам.
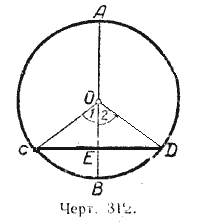
Пусть диаметр АВ перпендикулярен к хорде СD (черт. 312). Требуется доказать, что
СЕ = ЕD, 



Соединим точки С и D с центром окружности О. В равнобедренном треугольнике
СОD отрезок ЕО является высотой, проведённой из вершины О на основание СD; следовательно, ОЕ является и медианой и биссектрисой, т. е. СЕ = ЕD и / 1 = / 2. Но / 1 и / 2 суть центральные углы. Отсюда равны и соответствующие им дуги, а именно 

Теорема 2 (обрaтная). Диаметр, проведённый через середину хорды, не проходящей через центр, перпендикулярен к ней и делит дуги, стягиваемые хордой, пополам.
Пусть диаметр АВ делит хорду СD пополам. Требуется доказать, что АВ_|_СD, 



Соединим точки С и В с центром круга. Получим равнобедренный треугольник СОD, в котором ОК является медианой, а значит, и высотой. Следовательно, АВ_|_СD, а отсюда (по теореме 1) следует, что 



Теорема 3 (обратная).Диаметр, проведённый через середину дуги, делит пополам хорду, стягивающую эту дугу, и перпендикулярен к этой хорде.
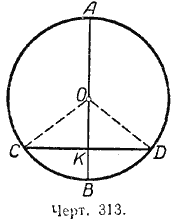
Пусть диаметр АВ делит дугу СВD пополам (черт. 313). Требуется доказать, что
СК = КD и АВ _|_ СD.
Соединим центр круга О с точками С и D. В равнобедренном треугольнике СОD отрезок ОК является биссектрисой угла СОD, так как по условию теоремы 

Видео:Радиус перпендикулярен хордеСкачать
Диаметр делит хорду пополам
Если диаметр делит хорду пополам, каково их взаимное расположение?
Если диаметр делит хорду пополам, то он перпендикулярен этой хорде.
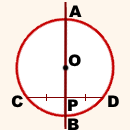
AB — диаметр, CD — хорда,

Так как OC=OD (как радиусы), то треугольник COD — равнобедренный с основанием CD.
Так как CP=PD, то OP — медиана треугольника COD, проведённая к основанию.
По свойству равнобедренного треугольника, OP является также его высотой.
🔍 Видео
7 класс. Геометрия. Теорема о перпендикулярности диаметра и хорды. 07.04.2020.Скачать

Радиус перпендикулярный хорде делит ее пополамСкачать

Окружность, диаметр, хорда геометрия 7 классСкачать

ОГЭ Задание 25 Теорема Фалеса Свойство диаметра и хордыСкачать

[10] Окружности с нуля для ЕГЭ по математике. Линия центров перпендикулярна общей хорде и делит...Скачать
![[10] Окружности с нуля для ЕГЭ по математике. Линия центров перпендикулярна общей хорде и делит...](https://i.ytimg.com/vi/OuPstDE05CQ/0.jpg)
Задание 26 Свойство секущих Свойство диаметра и хордыСкачать

Планиметрия 14 | mathus.ru | Хорда, делящаяся пополам.Скачать

Задание 25 В круге проведены две перпендикулярные хордыСкачать
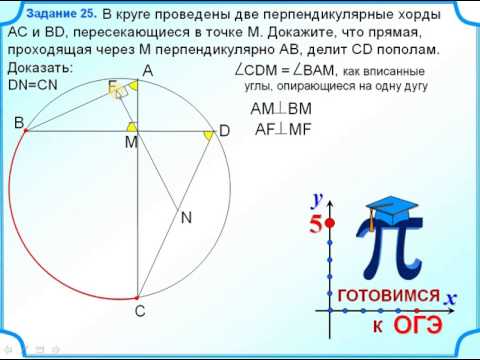
ОГЭ Задание 25 Окружность Касательная ХордаСкачать
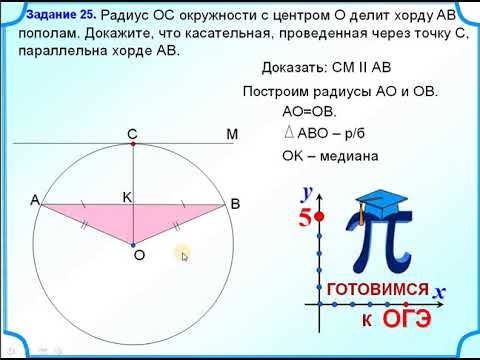
Радиус перпендикулярен хордеСкачать
Геометрия. Свойства окружности. Диаметр и хордаСкачать

Радиус перпендикулярный хорде делит ее пополамСкачать

Свойства хорд окружностиСкачать

№1,17 | Все теория по планиметрии за 4 часа | Решаем все прототипы №1 из ФИПИСкачать

Геометрия 8 класс за час. 4 часть. Взаимное расположение окружностей. Хорда.Кассательная.Скачать