Приведем формулу определения контактной прочности к удобному для нас виду. Ведем расчет зубчатой передачи в новых единицах, подставляя мощность в Вт, модуль в мм, вместо угловой скорости [рад/с]-частоту вращения [об/мин]. Итак, преобразуем для подстановки в формулу — m/1000 [м],2·π·n к /60 [рад/с]. Так как справочные таблицы для допускаемых напряжений у нас в кГ/мм 2 , то, используя равенство 9,8 Вт = 1 кГ·м/с, преобразуем полученное выражение в кГ/мм 2 . Тогда формула для рассчета зубчатого колеса на контактную прочность примет вид: τ с = [(В/z к ) 2 ·N к ·K·8·60·1000 3 / (2·π·n к ·m 3 ·q)] ½ / [9,8·1000 2 ] с ,
П ри выборе материала учитывают скорость скольжения v с червяка относительно колеса и нагрузку. При высоких скоростях (5 ÷ 25 м/с) выбирают сочетание стального закаленного, шлифованного и полированного червяка с бронзовым венцом колеса (центр колеса обычно выполняют из чугуна). При больших нагрузках червяки изготавливают из сталей марок 45 и 50 по ГОСТ 1050, из марок сталей 35 по ГОСТ 1050 и Ст.3 по ГОСТ 380. Венцы колес при высоких скоростях (5 ÷ 30 м/с) выполняют из бронз: в соответствии с ранее применявшимися обозначениями марки материала — оловянистой — Бр.ОФ 10-1 и оловяноникелевой Бр.ОНФ 11-4-3; с учетом новых обозначений — оловянно-фосфористых бронз БрО10Н1Ф1, БрО10Ф1, оловянно-цинковой бронзы БрО5Ц5С5. Содержание олова тем выше, чем больше Vc и продолжительность работы передачи. При средних скоростях ( 45). При малых скоростях скольжения (менее 2 м/с) и больших диаметрах колес допустимо применять чугуны марок СЧ15, СЧ20. Для твердых алюминиевожелезистых бронз допускаемые контактные напряжения выбирают из условий сопротивления заеданию в зависимости от скорости скольжения червяка.
И.Я. Левин «Справочник конструктора точных приборов»,Государственное научно-техническое издательство, М.,1962г.
Д.Н. Решетилов «Детали машин»,М.:Машиностроение, 1974г
web-сайт «ГРАФОАНАЛИТИЧЕСКИЕ СИСТЕМЫ» Контактная информация (e-mail): nomogramka@gmail.com
Copyright © 2005-2017 г. Все права защищены.
Видео:7.1 Червячные передачиСкачать

Диаметр делительной окружности червяка формула
юЕТЧСЮОБС РЕТЕДБЮБ (ТЙУХОПЛ 85) УПУФПЙФ ЙЪ ЮЕТЧСЛБ 1, Ф. Е. ЧЙОФБ У ФТБРЕГЕЙДБМШОПК ЙМЙ ВМЙЪЛПК Л ОЕК РП ЖПТНЕ ТЕЪШВПК, Й ЮЕТЧСЮОПЗП ЛПМЕУБ 2, Ф.Е. ЪХВЮБФПЗП ЛПМЕУБ У ЪХВШСНЙ ПУПВПК ЖПТНЩ, РПМХЮБЕНПК Ч ТЕЪХМШФБФЕ ЧЪБЙНОПЗП ПЗЙВБОЙС У ЧЙФЛБНЙ ЮЕТЧСЛБ.

юЕТЧСЮОЩЕ РЕТЕДБЮЙ ПФОПУСФУС Л ЮЙУМХ ЪХВЮБФП-ЧЙОФПЧЩИ, ЙНЕАЭЙИ ИБТБЛФЕТОЩЕ ЮЕТФЩ ЪХВЮБФЩИ Й ЧЙОФПЧЩИ РЕТЕДБЮ. ч ПФМЙЮЙЕ ПФ ЧЙОФПЧЩИ ЪХВЮБФЩИ РЕТЕДБЮ У РЕТЕЛТЕЭЙЧБАЭЙНЙУС ПУСНЙ, Х ЛПФПТЩИ ОБЮБМШОЩК ЛПОФБЛФ РТПЙУИПДЙФ Ч ФПЮЛЕ, Ч ЮЕТЧСЮОЩИ РЕТЕДБЮБИ ЙНЕЕФ НЕУФП МЙОЕКОЩК ЛПОФБЛФ. ч ПУЕЧПН УЕЮЕОЙЙ ЪХВШС ЛПМЕУБ ЙНЕАФ ДХЗПЧХА ЖПТНХ. ьФП ПВЕУРЕЮЙЧБЕФ ПВМЕЗБОЙЕ ФЕМБ ЮЕТЧСЛБ Й ХЧЕМЙЮЕОЙЕ ДМЙОЩ ЛПОФБЛФОЩИ МЙОЙК.
йЪПВТЕФЕОЙЕ ЮЕТЧСЮОЩИ РЕТЕДБЮ РТЙРЙУЩЧБАФ бТИЙНЕДХ.
дПУФПЙОУФЧБ ЮЕТЧСЮОЩИ РЕТЕДБЮ:
- ЧПЪНПЦОПУФШ РПМХЮЕОЙС ВПМШЫПЗП РЕТЕДБФПЮОПЗП ПФОПЫЕОЙС;
- РМБЧОПУФШ Й ВЕУЫХНОПУФШ ТБВПФЩ, ЧПЪНПЦОПУФШ ФПЮОЩИ ДЕМЙФЕМШОЩИ РЕТЕНЕЭЕОЙК.
оЕДПУФБФЛЙ ВПМШЫЙОУФЧБ ЮЕТЧСЮОЩИ РЕТЕДБЮ:
- ОЙЪЛЙК лрд;
- ОЕПВИПДЙНПУФШ РТЙНЕОЕОЙС ДМС ЛПМЕУБ ДПТПЗПУФПСЭЙИ БОФЙЖТЙЛГЙПООЩИ НБФЕТЙБМПЧ.
юЕТЧСЮОЩЕ РЕТЕДБЮЙ РТЙНЕОСАФ РТЙ ОЕПВИПДЙНПУФЙ УОЙЦЕОЙС УЛПТПУФЙ Й РЕТЕДБЮЙ ДЧЙЦЕОЙС НЕЦДХ РЕТЕЛТЕЭЙЧБАЭЙНЙУС (Ч ВПМШЫЙОУФЧЕ УМХЮБЕЧ ЧЪБЙНОП РЕТРЕОДЙЛХМСТОЩНЙ) ЧБМБНЙ. пВЯЕН РТЙНЕОЕОЙС ЮЕТЧСЮОЩИ РЕТЕДБЮ УПУФБЧМСЕФ ПЛПМП 10 % ПФ РЕТЕДБЮ ЪБГЕРМЕОЙЕН (ЪХВЮБФЩИ Й ЮЕТЧСЮОЩИ). чЩРХУЛ ЮЕТЧСЮОЩИ ТЕДХЛФПТПЧ РП ЮЙУМХ ЕДЙОЙГ УПУФБЧМСЕФ ПЛПМП РПМПЧЙОЩ ПВЭЕЗП ЧЩРХУЛБ ТЕДХЛФПТПЧ.
ыЙТПЛП РТЙНЕОСАФУС ЮЕТЧСЮОЩЕ РЕТЕДБЮЙ Ч РПДЯЕНОП-ФТБОУРПТФОЩИ НБЫЙОБИ, УФБОЛБИ, БЧФПНПВЙМСИ Й ДТХЗЙИ НБЫЙОБИ.
рЕТЕДБФПЮОПЕ ПФОПЫЕОЙЕ Й ЮЕТЧСЮОПК РЕТЕДБЮЙ ПРТЕДЕМСАФ ЙЪ ХУМПЧЙС, ЮФП ЪБ ЛБЦДЩК ПВПТПФ ЮЕТЧСЛБ ЛПМЕУП РПЧПТБЮЙЧБЕФУС ОБ ЮЙУМП ЪХВШЕЧ, ТБЧОПЕ ЮЙУМХ ЧЙФЛПЧ ЮЕТЧСЛБ:
ЗДЕ z1Й z2 — ЮЙУМП ЧЙФЛПЧ ЮЕТЧСЛБ Й ЮЙУМП ЪХВШЕЧ ЛПМЕУБ;
n1 Й n2 — ЮБУФПФЩ ЧТБЭЕОЙС ЮЕТЧСЛБ Й ЛПМЕУБ, НЙО -1 .
фБЛЙН ПВТБЪПН, РЕТЕДБФПЮОПЕ ЮЙУМП ОЕ ЪБЧЙУЙФ ПФ ПФОПЫЕОЙС ДЙБНЕФТПЧ ЮЕТЧСЛБ Й ЮЕТЧСЮОПЗП ЛПМЕУБ.
оБЙВПМШЫЕЕ ТБУРТПУФТБОЕОЙЕ РПМХЮЙМЙ ЮЕТЧСЮОЩЕ РЕТЕДБЮЙ У ГЙМЙОДТЙЮЕУЛЙНЙ ЮЕТЧСЛБНЙ.
пУОПЧОЩЕ РБТБНЕФТЩ ЮЕТЧСЮОЩИ ГЙМЙОДТЙЮЕУЛЙИ РЕТЕДБЮ. юЕТЧСЮОЩЕ РЕТЕДБЮЙ ЧУМЕДУФЧЙЕ ПФОПУЙФЕМШОП ОЙЪЛПЗП лрд РТЙНЕОСАФ ДМС ОЕВПМШЫЙИ Й УТЕДОЙИ НПЭОПУФЕК ПФ ДПМЕК ЛЙМПЧБФФБ ДП 200 ЛчФ, ЛБЛ РТБЧЙМП ДП 60 ЛчФ, ДМС НПНЕОФПЧ ДП 5·10 5 о· Н. рЕТЕДБФПЮОЩЕ ПФОПЫЕОЙС ПВЩЮОП РТЙОЙНБАФ ТБЧОЩНЙ ПФ 8 ДП 63. 80; Ч ПФДЕМШОЩИ УМХЮБСИ, ОБРТЙНЕТ Ч РТЙЧПДЕ УФПМПЧ ВПМШЫПЗП ДЙБНЕФТБ УФБОЛПЧ,- ДП 1000.
зпуф 2144-76* ХУФБОБЧМЙЧБЕФ УМЕДХАЭЙЕ ЪОБЮЕОЙС РЕТЕДБФПЮОЩИ ПФОПЫЕОЙК ЮЕТЧСЮОЩИ ТЕДХЛФПТПЧ:
ТСД 1-К . 8; 10; 12,5; 16; 20; 25; 31,5; 40; 50;63; 80
ТСД 2-К . 9; 11,2; 14; 18; 22,4; 28; 35,5; 45;56; 71
жБЛФЙЮЕУЛЙЕ ЪОБЮЕОЙС РЕТЕДБФПЮОЩИ ПФОПЫЕОЙК ОЕ ДПМЦОЩ ПФМЙЮБФШУС ВПМЕЕ ЮЕН ОБ 4 % ПФ ЪОБЮЕОЙК РП зпуфХ.
ъОБЮЕОЙС НПДХМЕК m, НН, ЧЩВЙТБАФ (РП зпуф 19672-74* Й зпуф 2144-76*) ЙЪ ТСДБ: 1, 1,25; 1,6; 2; 2,5; 3,15; 4; 5; 6,3; 8; 10; 12,5; 16; 20; 25; ДПРХУЛБАФУС m, ТБЧОЩЕ 1,5; 3; 3,5; 6; 7; 12 Й 14.
нЕЦПУЕЧЩЕ ТБУУФПСОЙС Бw (РП зпуф 2144-76*):
ТСД 1-К . 40; 50; 63; 80; 100; 125; 160; 200;250; 315; 400; 500
ТСД 2-К . . :. 140; 180; 225; 280; 355; 450 НН
зепнефтйс юетчсюощи гймйодтйюеулйи ретедбю
зЕПНЕФТЙЮЕУЛЙЕ ТБУЮЕФЩ ЮЕТЧСЮОЩИ РЕТЕДБЮ БОБМПЗЙЮОЩ ТБУЮЕФБН ЪХВЮБФЩИ РЕТЕДБЮ. чОБЮБМЕ ТБУУНБФТЙЧБЕН ЪБГЕРМЕОЙЕ ВЕЪ УНЕЭЕОЙС ЮЕТЧСЛБ.
ч УЧСЪЙ У ЙЪЗПФПЧМЕОЙЕН ЮЕТЧСЮОЩИ ЛПМЕУ ЙОУФТХНЕОФПН, СЧМСАЭЙНУС БОБМПЗПН ЮЕТЧСЛБ, УПРТСЦЕООЩК РТПЖЙМШ ЛПМЕУБ РПМХЮБЕФУС БЧФПНБФЙЮЕУЛЙ. рПЬФПНХ РТПЖЙМШ ЧЙФЛПЧ ЮЕТЧСЛБ НПЦОП ЧБТШЙТПЧБФШ. чЩВПТ РТПЖЙМС ПРТЕДЕМСЕФУС РТЕЙНХЭЕУФЧЕООП ФЕИОПМПЗЙЮЕУЛЙНЙ ЖБЛФПТБНЙ.
рТЙНЕОСАФ ЮЕТЧСЛЙ УМЕДХАЭЙИ ФЙРПЧ: БТИЙНЕДПЧЩ; ЛПОЧПМАФОЩЕ Й ВМЙЪЛЙЕ Л ОЙН — ОЕМЙОЕКЮБФЩЕ; ЬЧПМШЧЕОФОЩЕ, Б ФБЛЦЕ У ЧПЗОХФЩН РТПЖЙМЕН.
бТИЙНЕДПЧЩ ЮЕТЧСЛЙ (ТЙУХОПЛ 86, Б) РТЕДУФБЧМСАФ УПВПК ЧЙОФЩ У ТЕЪШВПК, ЙНЕАЭЕК РТСНПМЙОЕКОЩЕ ПЮЕТФБОЙС РТПЖЙМС (ФТБРЕГЙА) Ч ПУЕЧПН УЕЮЕОЙЙ (Ч ФПТГПЧПН УЕЮЕОЙЙ ЧЙФЛЙ ПЮЕТЮЕОЩ БТИЙНЕДПЧПК УРЙТБМША). ьФЙ ЮЕТЧСЛЙ РТПУФЩ Ч ЙЪЗПФПЧМЕОЙЙ, ЕУМЙ ОЕ ФТЕВХЕФУС ЙИ ЫМЙЖПЧБОЙЕ, РПЬФПНХ ПОЙ УПИТБОЙМЙ РТЙНЕОЕОЙЕ Ч ФЙИПИПДОЩИ, ОЕ УЙМШОП ОБРТСЦЕООЩИ РЕТЕДБЮБИ. дМС ЙИ ЫМЙЖПЧБОЙС ФТЕВХЕФУС ЛТХЗ, ПЮЕТЮЕООЩК УМПЦОПК ЛТЙЧПК Ч ПУЕЧПН УЕЮЕОЙЙ, ЮФП ПЗТБОЙЮЙЧБЕФ ЙИ РТЙНЕОЕОЙЕ.

рПД ЛПОЧПМАФОЩНЙ ЮЕТЧСЛБНЙ (ТЙУХОПЛ 86,6) РПОЙНБАФ ЮЕТЧСЛЙ, ЙНЕАЭЙЕ РТСНПМЙОЕКОЩК РТПЖЙМШ Ч УЕЮЕОЙЙ, ОПТНБМШОПН Л ПУЙ УЙННЕФТЙЙ. чЙФЛЙ Ч ФПТГПЧПН УЕЮЕОЙЙ ПЮЕТЮЕОЩ ХДМЙОЕООПК ЙМЙ ХЛПТПЮЕООПК ЬЧПМШЧЕОФПК. ьФЙ ЮЕТЧСЛЙ ПВМБДБАФ ОЕЛПФПТЩНЙ ФЕИОПМПЗЙЮЕУЛЙНЙ РТЕЙНХЭЕУФЧБНЙ РЕТЕД БТИЙНЕДПЧЩНЙ. рТЙ ФПЮЕОЙЙ ТЕЪШВЩ ДЧХУФПТПООЙН ТЕЪГПН (РП РТПЖЙМА ЛБОБЧЛЙ) РП ПВЕЙН ВПЛПЧЩН ЗТБОСН ТЕЪГБ ЙНЕАФ НЕУФП ПДЙОБЛПЧЩЕ ХЗМЩ ТЕЪБОЙС.
ыМЙЖПЧБОЙЕ ЛПОЧПМАФОЩИ ЮЕТЧСЛПЧ ЛПОХУОЩНЙ ЛТХЗБНЙ У РТСНПМЙОЕКОЩНЙ ПВТБЪХАЭЙНЙ ОБ ПВЩЮОЩИ ТЕЪШВПЫМЙЖПЧБМШОЩИ УФБОЛБИ РТЙЧПДЙФ Л РПМХЮЕОЙА ОЕМЙОЕКЮБФЩИ ВПЛПЧЩИ РПЧЕТИОПУФЕК, ЧЕУШНБ ВМЙЪЛЙИ Л РПЧЕТИОПУФСН ЛПОЧПМАФОЩИ ЮЕТЧСЛПЧ. юЕТЧСЮОЩЕ ЖТЕЪЩ ДМС ОБТЕЪБОЙС ЮЕТЧСЮОЩИ ЛПМЕУ ЫМЙЖХАФ ФЕН ЦЕ УРПУПВПН, РПЬФПНХ РПМХЮБАФ РТБЧЙМШОПЕ ЪБГЕРМЕОЙЕ. оБТЕЪБОЙЕ ТЕЪШВЩ ОЕМЙОЕКЮБФЩИ ЮЕТЧСЛПЧ РЕТЕД ЙИ ЫМЙЖПЧБОЙЕН ЛПОХУОЩН ЫМЙЖПЧБМШОЩН ЛТХЗПН НПЦЕФ ВЩФШ ПУХЭЕУФЧМЕОП ФБЛЦЕ ДЙУЛПЧПК ЖТЕЪПК.
ьЧПМШЧЕОФОЩЕ ЮЕТЧСЛЙ (ТЙУХОПЛ 86, Ч) РТЕДУФБЧМСАФ УПВПК ЛПУПЪХВЩЕ ЛПМЕУБ У НБМЩН ЮЙУМПН ЪХВШЕЧ Й ПЮЕОШ ВПМШЫЙН ХЗМПН ЙИ ОБЛМПОБ. рТПЖЙМШ ЪХВБ Ч ФПТГПЧПН УЕЮЕОЙЙ ПЮЕТЮЕО ЬЧПМШЧЕОФПК. ьЧПМШЧЕОФОБС РПЧЕТИОПУФШ ЙНЕЕФ РТСНПМЙОЕКОЩК РТПЖЙМШ Ч УЕЮЕОЙЙ РМПУЛПУФША, ЛБУБФЕМШОПК Л ПУОПЧОПНХ ГЙМЙОДТХ ЮЕТЧСЛБ, РПЬФПНХ ЬЧПМШЧЕОФОЩЕ ЮЕТЧСЛЙ НПЦОП ЫМЙЖПЧБФШ РМПУЛПК УФПТПОПК ЫМЙЖПЧБМШОПЗП ЛТХЗБ. ыМЙЖХЕНЩЕ ЮЕТЧСЛЙ УМЕДХЕФ ДЕМБФШ ЬЧПМШЧЕОФОЩНЙ.
юЕТЧСЮОЩЕ РЕТЕДБЮЙ ЙНЕАФ ХУМПЧОЩЕ ПВПЪОБЮЕОЙС: БТИЙНЕДПЧЩ Zб; ЛПОЧПМАФОЩЕ ZN; ОЕМЙОЕКЮБФЩЕ, РПМХЮЕООЩЕ ЫМЙЖПЧБОЙЕН ЛПОХУОЩН ЛТХЗПН, Zл; ЬЧПМШЧЕОФОЩЕ ZJ; У ЧПЗОХФЩН РТПЖЙМЕН ЮЕТЧСЛБ Zф.
ч ЮЕТЧСЮОЩИ РЕТЕДБЮБИ Ч УППФЧЕФУФЧЙЙ У зпуф 19036-81 УФБОДБТФОЩК ХЗПМ РТПЖЙМС РТЙОСФ ТБЧОЩН 20њ: Х БТИЙНЕДПЧЩИ ЮЕТЧСЛПЧ — Ч ПУЕЧПН УЕЮЕОЙЙ αИ, Х ЛПОЧПМАФОЩИ — Ч ОПТНБМШОПН УЕЮЕОЙЙ, Х ЬЧПМШЧЕОФОЩИ ЮЕТЧСЛПЧ, ЛБЛ Х ЛПУПЪХВЩИ ЛПМЕУ,- Ч ОПТНБМШОПН УЕЮЕОЙЙ ЛПУПЪХВПК ТЕКЛЙ, УГЕРМСАЭЕКУС У ЮЕТЧСЛПН, Х ОЕМЙОЕКЮБФЩИ — ХЗПМ РТПЖЙМС ЛПОЙЮЕУЛПК РТПЙЪЧПДСЭЕК РПЧЕТИОПУФЙ.
тБУУФПСОЙЕ НЕЦДХ ПДОПЙНЕООЩНЙ ФПЮЛБНЙ УППФЧЕФУФЧХАЭЙИ ВПЛПЧЩИ УФПТПО ДЧХИ УНЕЦОЩИ ЧЙФЛПЧ ЮЕТЧСЛБ, ЙЪНЕТЕООПЕ РБТБММЕМШОП ПУЙ, ОБЪЩЧБАФ ТБУЮЕФОЩН ЫБЗПН ЮЕТЧСЛБ Й ПВПЪОБЮБАФ ЮЕТЕЪ Т (ТЙУХОПЛ 87).

пФОПЫЕОЙЕ Т/π ОБЪЩЧБАФ НПДХМЕН m. нПДХМШ — УФБОДБТФОЩК РБТБНЕФТ; ДМС ЮЕТЧСЛБ ПО СЧМСЕФУС ПУЕЧЩН, ДМС ЮЕТЧСЮОПЗП ЛПМЕУБ — ФПТГПЧЩН.
юЕТЧСЮОЩЕ ЛПМЕУБ ОБТЕЪБАФ ЮЕТЧСЮОЩНЙ ЖТЕЪБНЙ, ТЕЦХЭЙЕ ЛТПНЛЙ ЛПФПТЩИ РТЙ ЧТБЭЕОЙЙ ЖТЕЪЩ ЙДЕОФЙЮОЩ У РПЧЕТИОПУФША ЧЙФЛПЧ ЮЕТЧСЛБ. рПЬФПНХ Ч ГЕМСИ УПЛТБЭЕОЙС ОПНЕОЛМБФХТЩ ЪХВПТЕЪОПЗП ЙОУФТХНЕОФБ УФБОДБТФЙЪПЧБОЩ ФБЛЦЕ ЛПЬЖЖЙГЙЕОФЩ ДЙБНЕФТБ ЮЕТЧСЛБ:
дЕМЙФЕМШОЩК ДЙБНЕФТ ЮЕТЧСЛБ (УН. ТЙУХОПЛ 87):
ЗДЕ q ЧЩВЙТБАФ РП зпуф 2144 — 76* Ч УПЮЕФБОЙЙ У НПДХМЕН m (ФБВМ. 21).
фБВМЙГБ 21. — ъОБЮЕОЙС НПДХМЕК Ф Ч ЪБЧЙУЙНПУФЙ ПФ ЛПЬЖЖЙГЙЕОФПЧ ДЙБНЕФТБ ЮЕТЧСЛБ q РТЙ z=1, 2, 4 (зпуф 2144-76*)
| m, НН | q |
| 2 | 8; 10; (12); 12,5; 16; 20 |
| 2,5 | 8; 10; (12); 12,5; 16; 20 |
| (3) | (10); (12) |
| 3,15 | 8; 10; 12,5; 16; 20 |
| (3,5) | (10); (12*); (14*) |
| 4 | 8; (9); 10; (12*); 12,5; 16; 20 |
| 5 | 8; 10; 12,5; 16; 20 |
| (6) | (9); (10) |
| 6,3 | 8; 10; 12,5; 16; 20 |
| (7) | (12) |
| 8 | 8; 10; 12,5; 16; 20 |
| 10 | 8; 10; 12,5; 16; 20 |
| (12) | (10**) |
| 12,5 | 8; 10; 12,5; 16; 20 |
| (14) | (8**) |
| 16 | 8; 10; 12,5; 16 |
| 20 | 8; 10 |
| *фПМШЛП РТЙ z1=1 | |
| **фПМШЛП РТЙ z1=1 Й 2 | |
| ***фПМШЛП РТЙ z1=2 | |
| рТЙНЕЮБОЙЕ. тСД ЪОБЮЕОЙК m Й q ХУФБОБЧМЙЧБЕФ зпуф 19672-74 *. ч ФБВМЙГЕ РТЙЧЕДЕОП ПЗТБОЙЮЕООПЕ ЮЙУМП НПДХМЕК. ъОБЮЕОЙС, ОЕ ЪБЛМАЮЕООЩЕ Ч УЛПВЛЙ, СЧМСАФУС РТЕДРПЮФЙФЕМШОЩНЙ | |
тЕЛПНЕОДХЕФУС ЧЩВЙТБФШ q=0,25z2 (РТЙ ЬФПН d1≈0,4Бw, ЗДЕ Бw— НЕЦПУЕЧПЕ ТБУУФПСОЙЕ), ФБЛ ЛБЛ ХЧЕМЙЮЕОЙЕ q РТЙЧПДЙФ Л УОЙЦЕОЙА лрд РЕТЕДБЮЙ, Б ХНЕОШЫЕОЙЕ — Л РБДЕОЙА ЙЪЗЙВОПК ЦЕУФЛПУФЙ ЮЕТЧСЛБ. дПРХУФЙНЩН УЮЙФБАФ ЪОБЮЕОЙС qmin=0,212z2
оБЮБМШОЩК ДЙБНЕФТ ЮЕТЧСЛБ ВЕЪ УНЕЭЕОЙС dw1 ТБЧЕО ДЕМЙФЕМШОПНХ ДЙБНЕФТХ d1.
юЙУМП ЧЙФЛПЧ ЮЕТЧСЛБ ЧЩВЙТБАФ Ч ЪБЧЙУЙНПУФЙ ПФ РЕТЕДБФПЮОПЗП ПФОПЫЕОЙС u. зпуф ХУФБОБЧМЙЧБЕФ z1 ТБЧОЩН 1, 2 Й 4. рЕТЕДБЮЙ ВПМШЫПК НПЭОПУФЙ ОЕ ЧЩРПМОСАФ У ЮЕТЧСЛБНЙ, ЙНЕАЭЙНЙ ПДЙО ЧЙФПЛ, ЙЪ-ЪБ НБМПЗП лрд Й УЙМШОПЗП ОБЗТЕЧБ.
хЗПМ РПДЯЕНБ МЙОЙЙ ЧЙФЛБ ЮЕТЧСЛБ ОБ ДЕМЙФЕМШОПН ГЙМЙОДТЕ γ (ДЕМЙФЕМШОЩК ХЗПМ РПДЯЕНБ):
чЩУПФБ ЗПМПЧЛЙ hБ1 Й ОПЦЛЙ hf1 ЧЙФЛПЧ ПРТЕДЕМСЕФУС РП ЖПТНХМБН:
ЗДЕ h*a1= ЛПЬЖЖЙГЙЕОФ ЧЩУПФЩ ЗПМПЧЛЙ,
h*f1 — ЛПЬЖЖЙГЙЕОФ ЧЩУПФЩ ОПЦЛЙ: ДМС БТИЙНЕДПЧЩИ, ЛПОЧПМАФОЩИ Й ОЕМЙОЕКЮБФЩИ ЮЕТЧСЛПЧ ТБЧЕО 1,2, Б ДМС ЬЧПМШЧЕОФОЩИ 1+0,2УПsγ.
дЙБНЕФТ тБУЛТПКФЕ УХФШ РПОСФЙС (148)
дМЙОХ b1 ОБТЕЪБООПК ЮБУФЙ ЮЕТЧСЛБ ЧЩВЙТБАФ ФЕН ВПМШЫЕК, ЮЕН ВПМШЫЕЕ ЮЙУМП ЪХВШЕЧ ЛПМЕУБ z2, Ф. Е.:
дМС ЫМЙЖХЕНЩИ Й ЖТЕЪЕТХЕНЩИ ЮЕТЧСЛПЧ ДМЙОХ b1 ХЧЕМЙЮЙЧБАФ ОБ 25 НН РТЙ НПДХМЕ m 16 НН (зпуф 19650-74).
юЕТЧСЮОЩЕ ЛПМЕУБ (ТЙУХОПЛ 88).
нЙОЙНБМШОЩЕ ЮЙУМБ ЪХВШЕЧ ЛПМЕУ z2min ЧП ЧУРПНПЗБФЕМШОЩИ ЛЙОЕНБФЙЮЕУЛЙИ РЕТЕДБЮБИ РТЙ ЮЕТЧСЛБИ У ПДОЙН ЧЙФЛПН РТЙОЙНБАФ ТБЧОЩНЙ 17. 18, Ч УЙМПЧЩИ РЕТЕДБЮБИ z2min=26. 28. пРФЙНБМШОП ДМС УЙМПЧЩИ РЕТЕДБЮ: z2=32. 63 (ОЕ ВПМЕЕ 80). ч РТЙЧПДБИ УФПМПЧ ВПМШЫПЗП ДЙБНЕФТБ z2 ДПИПДЙФ ДП 200. 300, Ч ПФДЕМШОЩИ УМХЮБСИ ДП 1000.

дЕМЙФЕМШОЩК Й УПЧРБДБАЭЙК У ОЙН ОБЮБМШОЩК ДЙБНЕФТ:
дЙБНЕФТ ЧЕТЫЙО dБ2 Й ЧРБДЙО df2 Ч УТЕДОЕН УЕЮЕОЙЙ Ч РЕТЕДБЮБИ ВЕЪ УНЕЭЕОЙС ЮЕТЧСЛБ УППФЧЕФУФЧЕООП ТБЧОЩ:
ч РЕТЕДБЮБИ У ЮЙУМПН ЧЙФЛПЧ ЮЕТЧСЛБ ДЧБ Й ВПМЕЕ ЬЖЖЕЛФЙЧОПЕ РПМЕ ЪБГЕРМЕОЙС ВПМШЫЕ, ЮЕН Ч РЕТЕДБЮЕ, ЮЕТЧСЛ ЛПФПТПК ЙНЕЕФ ПДЙО ЧЙФПЛ, РПЬФПНХ ОБТХЦОЩК ДЙБНЕФТ Й ЫЙТЙОХ ЛПМЕУБ ВЕТХФ НЕОШЫЙНЙ (РТЙ ФЕИ ЦЕ dБ2, d2 Й m). оБЙВПМШЫЙК ДЙБНЕФТ ЛПМЕУБ:

хУМПЧОЩК ХЗПМ ПВИЧБФБ 2δ ДМС ТБУЮЕФБ ОБ РТПЮОПУФШ ОБИПДСФ РП ФПЮЛБН РЕТЕУЕЮЕОЙС ПЛТХЦОПУФЙ da1-0,5m У ФПТГПЧЩНЙ (ЛПОФХТОЩНЙ) МЙОЙСНЙ ЮЕТЧСЮОПЗП ЛПМЕУБ:

нЕЦПУЕЧПЕ ТБУУФПСОЙЕ РЕТЕДБЮЙ ПВПЪОБЮБАФ ЮЕТЕЪ Бw, ПОП ТБЧОП РПМХУХННЕ ДЙБНЕФТПЧ ДЕМЙФЕМШОЩИ ПЛТХЦОПУФЕК ЮЕТЧСЛБ Й ЛПМЕУБ:

тбуюефщ об ртпюопуфш
юЕТЧСЮОЩЕ РЕТЕДБЮЙ ТБУУЮЙФЩЧБАФ ОБ УПРТПФЙЧМЕОЙЕ ХУФБМПУФЙ Й УФБФЙЮЕУЛХА РТПЮОПУФШ РП ЛПОФБЛФОЩН ОБРТСЦЕОЙСН Й ОБРТСЦЕОЙСН ЙЪЗЙВБ. ч ВПМШЫЙОУФЧЕ УМХЮБЕЧ ОБРТСЦЕОЙС ЙЪЗЙВБ ОЕ ПРТЕДЕМСАФ ТБЪНЕТЩ РЕТЕДБЮЙ Й ТБУЮЕФ РП ОЙН РТЙНЕОСАФ Ч ЛБЮЕУФЧЕ РТПЧЕТПЮОПЗП. пО ЪОБЮЙН ФПМШЛП РТЙ ВПМШЫЙИ ЮЙУМБИ ЪХВШЕЧ ЛПМЕУ (ВПМЕЕ 90. 100) Й ДМС ТХЮОЩИ РЕТЕДБЮ. пУОПЧОПЕ ЪОБЮЕОЙЕ ЙНЕЕФ ТБУЮЕФ ОБ УПРТПФЙЧМЕОЙЕ ЛПОФБЛФОПК ХУФБМПУФЙ, ЛПФПТЩК ДПМЦЕО РТЕДПФЧТБЭБФШ Ч РТПЕЛФЙТХЕНЩИ РЕТЕДБЮБИ ЧЩЛТБЫЙЧБОЙЕ, Й ТБУЮЕФ ОБ ЪБЕДБОЙЕ. тБУЮЕФ ОБ ЙЪОПУ УПЧНЕЭБАФ У ЬФЙН ТБУЮЕФПН.
лпоуфтхлгйй юетчсюощи тедхлфптпч
пУОПЧОПЕ ТБУРТПУФТБОЕОЙЕ ЙНЕАФ ПДОПУФХРЕОЮБФЩЕ ЮЕТЧСЮОЩЕ ТЕДХЛФПТЩ. дЙБРБЪПО РЕТЕДБФПЮОЩИ ПФОПЫЕОЙК u=8. 63. рТЙ ВПМШЫЙИ РЕТЕДБФПЮОЩИ ЮЙУМБИ РТЙНЕОСАФ ДЧХИУФХРЕОЮБФЩЕ ЮЕТЧСЮОЩЕ ТЕДХЛФПТЩ ЙМЙ ЛПНВЙОЙТПЧБООЩЕ ЪХВЮБФП-ЮЕТЧСЮОЩЕ ТЕДХЛФПТЩ.
тЕДХЛФПТЩ ЧЩРПМОСАФ УП УМЕДХАЭЙНЙ ЧБТЙБОФБНЙ ТБУРПМПЦЕОЙС ЮЕТЧСЛБ Й ЮЕТЧСЮОПЗП ЛПМЕУБ:
- ЮЕТЧСЛ РПД ЛПМЕУПН — РТЙНЕОСАФ РТЙ ПЛТХЦОЩИ УЛПТПУФСИ ЮЕТЧСЛБ ДП 4. 5 Н/У, УНБЪЛБ-ПЛХОБОЙЕН ЮЕТЧСЛБ (ТЙУХОПЛ 89, Б); ДПРХУЛБЕФ РЕТЕДБЮХ ВПМШЫЕК НПЭОПУФЙ РП ЛТЙФЕТЙА ОБЗТЕЧБ, ОП ИХЦЕ Ч ПФОПЫЕОЙЙ ХФЕЮЛЙ НБУМБ;
- ЮЕТЧСЛ ОБД ЛПМЕУПН — РТЕДРПЮФЙФЕМШОБС ЛПОУФТХЛГЙС, РТЙНЕОСЕНБС Ч ВЩУФТПИПДОЩИ РЕТЕДБЮБИ ЧП ЙЪВЕЦБОЙЕ ЙЪМЙЫОЙИ РПФЕТШ ОБ ТБЪВТЩЪЗЙЧБОЙЕ НБУМБ ВЩУФТПИПДОЩН ЮЕТЧСЛПН, УНБЪЛБ — ПЛХОБОЙЕН ЛПМЕУБ (ТЙУХОПЛ 89,6);
- ЮЕТЧСЛ У ЗПТЙЪПОФБМШОПК ПУША, УГЕРМСАЭЙКУС У ЛПМЕУПН, ЙНЕАЭЙН ЧЕТФЙЛБМШОХА ПУШ (ТЙУХОПЛ 89, Ч);
- ЮЕТЧСЛ У ЧЕТФЙЛБМШОПК ПУША, ТБУРПМПЦЕООПК УВПЛХ ЛПМЕУБ (ТЙУХОПЛ 89, З).
тЙУХОПЛ 89 — пУОПЧОЩЕ УИЕНЩ ПДОПУФХРЕОЮБФЩИ ЮЕТЧСЮОЩИ ТЕДХЛФПТПЧ.
дЧЕ РПУМЕДОЙЕ ЛПОУФТХЛГЙЙ РТЙНЕОСФШ ОЕЦЕМБФЕМШОП ЧУМЕДУФЧЙЕ ФТХДОПУФЙ УНБЪЩЧБОЙС РПДЫЙРОЙЛПЧ ЧЕТФЙЛБМШОЩИ ЧБМПЧ Й ХДЕТЦБОЙС УНБЪЛЙ ПФ ЧЩФЕЛБОЙС.
юЕТЧСЛЙ Ч УМХЮБЕ ОБТЕЪБОЙС ТЕЪШВЩ ТЕЪГПН ДПМЦОЩ ЙНЕФШ ЧЩИПД ДМС ЙОУФТХНЕОФБ (РТПФПЮЛХ). оБ ТЕЪШВПЖТЕЪЕТОПН УФБОЛЕ ТЕЪШВБ НПЦЕФ ВЩФШ ЙЪЗПФПЧМЕОБ УП УВЕЗПН.
юЕТЧСЮОЩЕ ЛПМЕУБ Ч ГЕМСИ ЬЛПОПНЙЙ ГЧЕФОЩИ НЕФБММПЧ ЧЩРПМОСАФ У ЧЕОГПН ЙЪ БОФЙЖТЙЛГЙПООЩИ НБФЕТЙБМПЧ Й УФБМШОЩН ЙМЙ ЮХЗХООЩН ГЕОФТПН.
рТЙНЕОСАФ УМЕДХАЭЙЕ ФЙРПЧЩЕ ЛПОУФТХЛГЙЙ:
 тЙУХОПЛ 90 — фЙРПЧЩЕ ЛПОУФТХЛГЙЙ ЪХВЮБФЩИ ЧЕОГПЧ ЮЕТЧСЮОЩИ ЛПМЕУ.
тЙУХОПЛ 90 — фЙРПЧЩЕ ЛПОУФТХЛГЙЙ ЪХВЮБФЩИ ЧЕОГПЧ ЮЕТЧСЮОЩИ ЛПМЕУ.ч ЮЕТЧСЮОЩИ РЕТЕДБЮБИ, ЛБЛ РТБЧЙМП, РТЙНЕОСАФ РПДЫЙРОЙЛЙ ЛБЮЕОЙС.
юЕТЧСЛЙ У ОЕВПМШЫЙН ТБУУФПСОЙЕН НЕЦДХ ПРПТБНЙ Ч РЕТЕДБЮБИ, ОЕ ОБРТСЦЕООЩИ Ч ФЕРМПЧПН ПФОПЫЕОЙЙ, ДПРХУЛБЕФУС ХУФБОБЧМЙЧБФШ ОБ ТБДЙБМШОП-ХРПТОЩИ РПДЫЙРОЙЛБИ РП ПДОПНХ Ч ПРПТЕ (ХУФБОПЧЛБ «ЧТБУРПТ») (ТЙУХОПЛ 91, Б). х ЮЕТЧСЛПЧ У ВПМШЫЙН ТБУУФПСОЙЕН НЕЦДХ ПРПТБНЙ, ТБВПФБАЭЙИ Ч ОБРТСЦЕООПН ФЕРМПЧПН ТЕЦЙНЕ, УФБЧСФ Ч ПДОПК ПРПТЕ РМБЧБАЭЙК РПДЫЙРОЙЛ, Б Ч ДТХЗПК — ДЧБ ТБДЙБМШОП-ХРПТОЩИ ЙМЙ ПДЙО УДЧПЕООЩК, ЧПУРТЙОЙНБАЭЙЕ ПУЕЧЩЕ ХУЙМЙС Ч ПВПЙИ ОБРТБЧМЕОЙСИ (ТЙУХОПЛ 91, 6).
дМС ЧБМБ ЮЕТЧСЮОПЗП ЛПМЕУБ ЧЧЙДХ ЕЗП ОЕВПМШЫПК ДМЙОЩ РТЙНЕОСАФ РП ПДОПНХ ТБДЙБМШОП-ХРПТОПНХ (ПВЩЮОП ЛПОЙЮЕУЛПНХ ТПМЙЛПЧПНХ) РПДЫЙРОЙЛХ Ч ПРПТЕ, ЛПФПТЩЕ ХУФБОБЧМЙЧБАФ ЧТБУРПТ.
лПТРХУБ ЛТХРОЩИ ТЕДХЛФПТПЧ ДЕМБАФ У ЧЕТИОЕК ЛТЩЫЛПК, Б НБМЩИ — У ВПЛПЧПК ЛТЩЫЛПК. лПТРХУБ ДЕМБАФ ЮХЗХООЩНЙ Й БМАНЙОЙЕЧЩНЙ.
Видео:Лекция 5. Червячные передачиСкачать

Диаметр делительной окружности червяка формула
Классификация червячных передач. По исполнению червячные передачи различают четыре вида по расположению червяка относительно червячного колеса, а также разделяются на открытые и закрытые (рис. 89).
Рис. 89. Классификация червячных передач по расположению червяка: а – с нижним расположением червяка, б – с верхним расположением червяка, в – с боковым расположением червяка, г – с вертикальным расположением чкервяка.
По назначению червячные передачи делятся на кинематические и силовые. По форме наружной поверхности червяка различают два основных вида червячных передач: цилиндрические, или просто червячные передачи (с цилиндрическими червяками) и глобоидные (с глобоидными червяками). В зависимости от формы профиля резьбы цилиндрических червяков различают червяки: архимедовы (


Рис.90. Классификация по форме профиля червяка: а – цилиндрический архимедов, б – глобоидный, в – цилиндрический эвольвентный, г — с вогнутым профилем витков.
Назначение. Червячные передачи относится к механическим передачам зацепления с непосредственным контактом и предназначены для передачи вращательного движения между скрещивающимися валами (с углом, как правило 900) при необходимости реализации больших передаточных чисел (
Преимущества. Возможность передачи вращения между скрещивающимися валами и получения больших передаточных чисел в малых габаритах одной пары зацепления. Плавность и бесшумность работы. Компактность и простота эксплуатации. Возможность самоторможения. Высокая кинематическая точность.
Недостатки. Относительно низкий КПД. Большие потери мощности, что не позволяет использовать для передачи больших нагрузок и мощностей. Повышенный износ и склонность к заеданию контактирующих поверхностей. Необходимость применения дорогостоящих антифрикционных материалов и режущих инструментов, что повышает стоимость передачи относительно зубчатых.
Сферы применения. Червячные передачи применяются при мощности до 60кВт, в некоторых случаях до 200кВт, при передаточном числе 

Геометрический расчет. Для червяков и колес червячных цилиндрических передач модуль т, мм, нормализован по ряду: 1,0; 1,25; 1,6; 2,0; 2,5; 3,15; 4,0; 5,0; 6,3; 8,0; 10,0; 12,5; 16,0; 20,0; 25,0.
Передаточное отношение передачи

где 
Число витков червяка принимают в зависимости от передаточного отношения передачи:
— 

— 

— 
Для червячных передач номинальные значения передаточных чисел и стандартизованы ГОСТ2185 — 66 Номинальные значения передаточных чисел и для червячных редукторов следующие:
1-й ряд 1,00; 1,25; 1,60; 2,00; 2,50; 3,15; 4,0; 5,0; 6,3; 8,0; 10,0;12,5; 16; 20.
2-й ряд 1,12; 1,40; 1,80; 2,24; 2,80; 3,55; 4,5; 5,6; 7,1; 9,0; 11,2; 14; 18; 22,4.
При выборе стандартных параметров первый ряд предпочтительнее второго, а принятые значения передаточных чисел для червячных передач не должны отличаться от расчетных не более чем на 4%.
Для червячных цилиндрических передач с углом скрещивания осей червяка и колеса, равным 90° по ГОСТ 2144 — 76 нормализованы: делительные углы подъема витков червяка, длина червяка и межосевые расстояния:
1-й ряд 
2-й ряд 
Размеры червячного колеса определяются по таким же расчетным зависимостям как для зубчатых колес. Для унификации стандартного инструмента, применяемого при нарезании червяков и червячных колес, отношение делительного диаметра 



Стандартом установлено два ряда значений коэффициентов диаметра червяка q:
1-й ряд 6,3; 8; 10; 12,5; 16; 20; 25;
2-й ряд 7,5; 9; 11,2; 14; 18; 22,4.
В мелкомодульных передачах коэффициент диаметра червяка q рекомендуется брать больше, так как червяки в них могут оказаться недостаточно жесткими.
Тангенс делительного угла подъема витков червяка и угла наклона зубьев колеса

Значения делительного угла подъема витков червяка в зависимости от его параметров приведены в таблице 15.1.
Таблица 15.1 Делительный угол подъема витков червяка
Основные геометрические параметры червячной передачи без смещения показаны на рис. 91 определяются по зависимостям:
— делительные и начальные диаметры червяка и колеса:


— диаметры вершин червяка и колеса:


— диаметры впадин червяка и колеса:


Рис. 91. Геометрические параметры червячной передачи
В червячной передаче без смещения высота зубьев и витков

Для передачи без смещения делительное межосевое расстояние а и межосевое расстояние aw:

Модуль червячного зацепления проверяется по зависимости

Наибольший диаметр червячного колеса определяется по формуле

Условный угол обхвата 

Длина нарезанной части червяка принимают:
при 

при 

Ширина венца зубчатого колеса
при 
при 
Остальные размеры зубчатого колеса принимаются такими как для зубчатых колес. Смещение цилиндрической червячной передачи с архимедовым червяком осуществляется только за счет колеса, размеры червяка, за исключением диаметра начального цилиндра, не изменяются. Предельное значение коэффициента смещения при отсутствии подрезания и заострения зубьев червячного колеса рекомендуется принимать 
Минимальное число зубьев колеса в силовой червячной передаче принимают =26. 28. При выборе и в зависимости от передаточного числа и необходимо иметь в виду, что для передачи без смещения во избежание подрезания зубьев колеса должно быть z2 > 28.
Кинематический и силовой расчеты. Векторы окружных скоростей червяка 


От окружной скорости колеса зависит выбор степени точности передачи. Из 12 степеней точности изготовления червячных передач, регламентируемых ГОСТ 13675-68 для силовых передач предусмотрены 5, 6, 7, 8 и 9-я степени точности. В общем машиностроении чаще всего пользуются 7, 8 и 9-й степенями точности. Выбор степени точности червячной передачи в зависимости от окружной скорости колеса 
Таблица 15.2. Степени точности червячных передач
Окружная скорость колеса υ, м/с, не более
Червяк закален, отшлифован и отполирован. Колесо нарезают шлифованными червячными фрезами. Обработка под нагрузкой
Передачи с повышенными скоростями и малым шумом, высокими требованиями к габаритам
Червяк с НВ≤350 нешлифованный. Колесо нарезают нешлифованной червячной фрезой или «летучкой». Обработка под нагрузкой
Передачи среднескоростные со средними требованиями к шуму, габаритам и точности
Червяк с НВ≤350 нешлифованный. Колесо нарезают любым способом
Передачи низкоскоростные, кратковременно работающие, и ручные с пониженными требованиями
Скорость скольжения представляет собой геометрическую разность этих скоростей и определяется по формуле

или по зависимости

Выбор материала червячного колеса в основном зависит от скорости скольжения витков резьбы червяка по зубьям колеса.
Сила взаимодействия между витками резьбы червяка и зубьями червячного колеса может быть разложена на три взаимно перпендикулярные составляющие: окружную, осевую и радиальную силы. Окружная сила червяка 


Окружная сила 


Радиальная сила 

где 
Коэффициент полезного действия червячного редуктора при ведущем червяке с учетом потерь в зацеплении, в опорах и наразбрызгивание и перемешивание масла

Коэффициент полезного действия червячного редуктора при ведущем колесе с учетом изменения направления сил трения

Значения коэффициента трения, а следовательно и приведенного угла трения принимается в зависимости от скорости скольжения в передаче. Приведенные углы трения при работе червячного колеса из оловянистой бронзы по стальному червяку даны в табл.15.3.
Таблица 15.3 Приведенные углы трения
φ’
φ’
Критерии работоспособности. Учитывая виды повреждений основными критериями работоспособности червячной передачи являются контактная и изгибная прочность зубьев червячного колеса. В связи с тем что поверхностное разрушение зубьев колеса зависит от контактных напряжений, а поломка — от напряжений изгиба, зубья червячных колес, так же как и зубья зубчатых колес, рассчитывают на прочность по контактным напряжениям и напряжениям изгиба. При проектировочном расчете червячных передач редукторов определяют требуемое по условию контактной прочности межосевое расстояние передачи; затем проверяют зубья колеса на изгиб. В большинстве случаев оказывается, что расчетные напряжения изгиба значительно ниже допускаемых. Лишь в случае мелко — модульного зацепления при большом числе зубьев колеса (z2 > 100) может оказаться, что прочность на изгиб недостаточна. При этом приходится изменить размеры зацепления и вновь производить проверку. Помимо указанных расчетов для червячных передач выполняют расчет червяка на жесткость и тепловой расчет червячного редуктора.
Проектные расчеты червячных передач.
Расчет зубьев на контактную прочность. При проектировочном расчете зубьев червячных колес на контактную прочность определяется межосевое расстояние передачи:

где 



Число зубьев колеса 





После определения расчетного межосевого расстояния его значения округляют до ближайшего стандартного. Находят модуль зацепления по зависимости (15.11) и полученное значение округляют до ближайшего стандартного. Для получения стандартных размеров передачи найденные значения корректируют величиной межосевого расстояния либо коэффициентом диаметра червяка 

Допускаемое контактное напряжение 

где 





Коэффициент долговечности KHL определяют в зависимости от отношения 





Если при расчете 


Таблица 15.4 Механические характеристики материалов червячных колес
📽️ Видео
Модуль шестерни и параметры зубчатого колесаСкачать

Что такое МОДУЛЬ шестерни? Ты ТОЧНО поймешь!Скачать

Расчет червячной передачи.Расчет червяка.Чертеж червякаСкачать

Правильное червячное колесо летучкой на зуборезе.Для питчевого червяка DP13. Теория и практика.Скачать

Лекция «Червячные передачи»Скачать

ЧЕРВЯЧНАЯ ПЕРЕДАЧА ➤ Классификация ➤ Достоинства и недостаткиСкачать

6.3 Зубчатые цилиндрические передачиСкачать

Конические и червячные передачи, каф. МеханикаСкачать
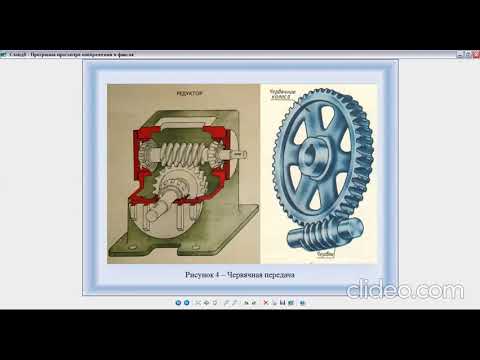
Азбука "ВиМП", часть 8. Червячная цилиндрическая передачаСкачать

Расчет червячной передачи.Расчет червячного колеса.Чертеж червячного колесаСкачать
Детали машин. Лекция 2.5. Червячные передачиСкачать

Азбука "ВиМП", часть 9. Червячная глобоидная передачаСкачать

Лекция 4. Конические зубчатые передачиСкачать

Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Лекальные кривые. Спираль Архимеда. Эвольвента окружности. ЦиклоидаСкачать

Определение передаточного числа червячной пары Подольск_ПриводСкачать

Как пользоваться делительным диском на УДГСкачать

Длина общей нормали. Измерение и программа для расчетаСкачать


 тЙУХОПЛ 89 — пУОПЧОЩЕ УИЕНЩ ПДОПУФХРЕОЮБФЩИ ЮЕТЧСЮОЩИ ТЕДХЛФПТПЧ.
тЙУХОПЛ 89 — пУОПЧОЩЕ УИЕНЩ ПДОПУФХРЕОЮБФЩИ ЮЕТЧСЮОЩИ ТЕДХЛФПТПЧ.










