Укажите номера верных утверждений.
1) Диаметр делит окружность на две равные дуги.
2) Параллелограмм имеет две оси симметрии.
3) Площадь треугольника равна его основанию, умноженному на высоту.
Проверим каждое из утверждений.
1) «Диаметр делит окружность на две равные дуги» — верно, по свойству диаметра.
2) «Параллелограмм имеет две оси симметрии» — неверно. Параллелограмм имеет центр симметрии, этим центром является точка пересечениия диагоналей параллелграмма.
3) «Площадь треугольника равна его основанию, умноженному на высоту» — неверно, площадь треугольника равна половине произведения основания на высоту.
Аналоги к заданию № 311851: 316323 316349 316375 Все
Видео:КАК НАЙТИ ДИАМЕТР ОКРУЖНОСТИ, ЕСЛИ ИЗВЕСТНА ДЛИНА ОКРУЖНОСТИ? Примеры | МАТЕМАТИКА 6 классСкачать

Радиус и диаметр окружности — определение двух отрезков
На практике в жизни с окружностью сталкивается каждый человек. Это может быть обруч, который крутят на уроке физкультуры либо на занятиях фитнеса, а также арена цирка либо просто украшение на пальце — кольцо. Радиус и диаметр окружности — взаимосвязанные математические понятия, которые необходимо выучить детям в школьной программе еще в начальной школе.
Видео:Длина окружности. Математика 6 класс.Скачать

Определения понятий
Чтобы изобразить фигуру, достаточно обвести контур карандашом вокруг круглого предмета либо начертить при помощи циркуля. На месте прокола циркуля ставят точку, что и будет центром окружности.
Окружность — геометрическое место точек плоскости, в котором длина от точек к центру одинаковая. По-другому можно описать определение, что это замкнутая кривая, в которой править будут равные отрезки, проведенные от центра до краев фигуры. Круг — часть плоскости, которая ограничена окружностью.
Если поставить точку на окружности и соединить ее с центром, в результате получится отрезок. Таких отрезков можно нарисовать не один, сколько точек на окружности поставить — столько и будет таких отрезков, то есть бесчисленное количество.
Отрезок, который равен расстоянию от центра до границ окружности имеет название радиуса. Этот термин с латинскими корнями и в переводе означает луч либо спица колеса.
Первый раз о термине заговорили в 1569 году, и примерно через 100 лет он стал общепринятым. И не удивительно, так как в обиходе люди часто говорят, к примеру, «пожар в радиусе 10 км уничтожил все», «в радиусе 5 м нет видимости» и так далее.
Диаметром называется отрезок, который соединяет 2 точки окружности и проходит обязательно через центр круга. Такой отрезок делит круг на 2 части. По-другому — хорда, которая проходит через центр круга. Этот отрезок самый больший, который можно изобразить в круге, что и будет отличаться от других отрезков. Их можно изобразить в фигуре бесконечное число.
Видео:ЕГЭ Математика Задание 6#27935Скачать

Обозначения и свойства
Понятия имеют принятые обозначения. Буквой d обозначают диаметр (в некоторых источниках обозначается перечеркнутой буквой о), а r — радиус. Для измерения используют:
Диаметр состоит из 2 радиусов, а это значит, если необходимо узнать, чему равен радиус, необходимо длину диаметра разделить напополам. То есть разница между ними в 2 раза. Не всегда два радиуса образуют диаметр: только при условии, если они находятся на одной прямой.
Для решений задач можно использовать формулу: d =2*r. Естественно, формула работает в обратном направлении, она будет выглядеть следующим образом: r = d/2.
Дано: r =80 мм, определить, на сколько сантиметров диаметр длиннее. Для решения задачи используют формулу d=2*r. Но для начала необходимо перевести миллиметры в сантиметры. 80 мм=8 см. Далее d=2*8=16 см. Чтобы вычислить отличие, необходимо 16−8=8 см. Ответ — на 8 см длиннее.
Видео:Найти радиус равнобедренного прямоугольного треугольника 3 задание проф. ЕГЭ по математикеСкачать

Дополнительные сведения
Если в окружности провести 2 радиуса, то в результате круг будет разделен на 2 части, которые называются секторами. Отрезки образуют центральный угол.
Если в точке пересечения радиуса с поверхностью =начертить касательную, то обе линии будут перпендикулярными по отношению друг к другу. Если провести к хорде так, чтобы между ними образовался угол 90 0 , то в точке пересечения хорда будет разделена на 2 части. Если с хордой пересекается диаметр под углом 90 0 , то хорда и дуга будут разделены на две равные части.
Видео:Уравнение окружности (1)Скачать

Всё про окружность и круг
Окружность — это геометрическое место точек плоскости, равноудаленных от некоторой заданной точки (центра окружности). Расстояние между любой точкой окружности и ее центром называется радиусом окружности (радиус обозначают буквой R).
Значит, окружность — это линия на плоскости, каждая точка которой расположена на одинаковом расстоянии от центра окружности.
Кругом называется часть плоскости, ограниченная окружностью и включающая ее центр.
Отрезок, соединяющий две точки окружности, называется хордой. Хорда, проходящая через центр окружности, представляет собой диаметр. Диаметр окружности равен ее удвоенному радиусу: D = 2R.
Точка пересечения двух хорд делит каждую хорду на отрезки, произведение которых одинаково: a1a2 = b1b2
Касательная к окружности всегда перпендикулярна радиусу, проведенному в точку касания.
Отрезки касательных к окружности, проведенные из одной точки, равны: AB = AC, центр окружности лежит на биссектрисе угла BAC.
Квадрат касательной равен произведению секущей на ее внешнюю часть
Центральный угол — это угол, вершина которого совпадает с центром окружности.
Дугой называется часть окружности, заключенная между двумя точками.
Мерой дуги (в градусах или радианах) является центральный угол, опирающийся на данную дугу.
Вписанный угол это угол, вершина которого лежит на окружности, а cтороны угла пересекают ее.
Вписанный угол равен половине центрального, если оба угла опираются на одну и ту же дугу окружности.
Внутренние углы, опирающиеся на одну и ту же дугу, равны.
Сектором круга называется геометрическая фигура, ограниченная двумя радиусами и дугой, на которую опираются данные радиусы.
Периметр сектора: P = s + 2R.
Площадь сектора: S = Rs/2 = ПR 2 а/360°.
Сегментом круга называется геометрическая фигура, ограниченная хордой и стягиваемой ею дугой.
📹 Видео
Длина окружности. Практическая часть - решение задачи. 6 класс.Скачать

Определение центра дуги окружности, построение окружности по 3 точкамСкачать

Деление окружности на 3, 4, 5, 6 и 7 равных частейСкачать

Как Эратосфен измерил диаметр Земли?Скачать

ОГЭ 2023 Ященко 2 вариант ФИПИ школе полный разбор!Скачать

Нафиг теорему синусов 3 задание проф. ЕГЭ по математике (часть I)Скачать

Вершины треугольника делят окружность на три дуги, длины которых относятся как 3:4:11Скачать

Вся геометрия 7–9 класс с нуля | ОГЭ МАТЕМАТИКА 2023Скачать

Геометрия с Нуля (первая часть)Скачать

Деление окружности на равные части. Урок 6. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

✓ Три окружности | Планиметрия | Олимпиада Ломоносов-2020 | Борис ТрушинСкачать

Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать

ВСЕ правила и формулы ПЛАНИМЕТРИИСкачать

ОГЭ 2024 Ященко 15 вариант ФИПИ школе полный разбор!Скачать

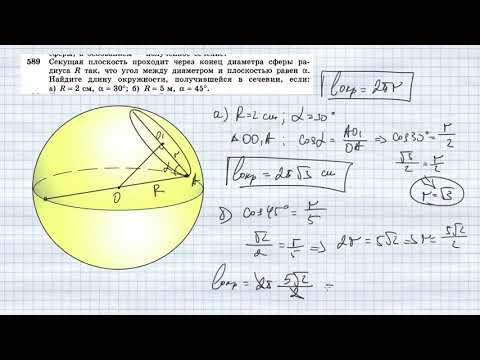
№589. Секущая плоскость проходит через конец диаметра сферы радиуса R так, что угол между диаметромСкачать