Диаграмма эйлера венна для треугольников

Множества изображаются в виде кругов или эллипсов, помещенных в прямоугольник (универсум).

Универсальное множество (универсум) U — множество, содержащее все элементы рассматриваемых подмножеств и элементы, не входящие в них.
Пустое множество Ø — множество, не содержащее ни одного элемента рассматриваемых подмножеств.
Количество пересечений (областей) n определяется по формуле: n=2 N ,
где N — количество множеств.

Видео:Простое объяснения решения задач при помощи кругов ЭйлераСкачать

Рисование кругов Эйлера

Видео:Как изображать множества на диаграммахСкачать

Алгоритм построения диаграмм Эйлера-Венна

1. Определяют количество подмножеств ( А , В , С , D ).
2. На диаграмме строят пересекающиеся множества, включенных в универсум.
3. Выделяют области, количество которых равно количеству пересечений.

Видео:Круги Эйлера в реальной жизни. Математика на QWERTYСкачать

Диаграммы Эйлера-Венна для одного множества А

На последнем рисунке приведены соответствующие области таблицы истинности, которая состоит из n=2 1 = 2 строк (областей)
Примеры
Универсум U=, А=
A = , A ∩ A = ∩ = = Ø

Видео:Доказать равенства при помощи диаграмм Эйлера-Венна. Действия над множествами.Скачать

Диаграммы Эйлера-Венна для двух множеств А и В

На последнем рисунке приведены соответствующие области таблицы истинности, которая состоит из n=2 2 = 4 строк (областей)
Примеры
Универсум U=, А=, В=
A∪B = ∪ =

Видео:Доказать равенства при помощи диаграмм ВеннаСкачать

Диаграммы Эйлера-Венна для трех множеств А , В , С

На последнем рисунке приведены соответствующие области таблицы истинности, которая состоит из n=2 3 = 8 строк (областей)
Примеры
Универсум U=, А=, В=, C=
BC ∪ A = ∪ = ∪ =

Видео:Математика. 3 класс. Множества. ПодмножестваСкачать

Диаграммы Эйлера-Венна для четырех множеств А , В , С , D

На последнем рисунке приведены соответствующие области таблицы истинности, которая состоит из n=2 4 = 16 строк (областей)
Примеры
Универсум U=
А=
В=
C=
D=

Видео:Введение в теорию вероятности. Диаграмма Венна.Скачать

Тема: «Диаграмма Эйлера-Венна»

Федеральное агентство по образованию

Государственное образовательное учреждение высшего профессионального образования

Томский политехнический университет

Студент группы 2У00

3. Операции над множествами диаграммы Эйлера-Венна………………….5

b) Пересечение, дополнение………………….……………………………..7

c) Стрелка Пирса, штрих Шеффера и разность. ………………………….8

e) Симметрическая разность и эквивалентность…………………….…….9

Круги Эйлера — геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления. Круги были изобретены Леонардом Эйлером. Используется в математике, логике, менеджменте и других прикладных направлениях.

Важный частный случай кругов Эйлера — диаграммы Эйлера — Венна, изображающие все 2n комбинаций n свойств, то есть конечную булеву алгебру. При n = 3 диаграмма Эйлера — Венна обычно изображается в виде трёх кругов с центрами в вершинах равностороннего треугольника и одинаковым радиусом, приблизительно равным длине стороны треугольника.

При решении целого ряда задач Леонард Эйлер использовал идею изображения множеств с помощью кругов. Однако этим методом ещё до Эйлера пользовался выдающийся немецкий философ и математик (1646—1716). Лейбниц использовал их для геометрической интерпретации логических связей между понятиями, но при этом всё же предпочитал использовать линейные схемы.

Но достаточно основательно развил этот метод сам Л. Эйлер. Методом кругов Эйлера пользовался и немецкий математик Эрнст Шрёдер (1841—1902) в книге «Алгебра логики». Особенного расцвета графические методы достигли в сочинениях английского логика Джона Венна (1843—1923), подробно изложившего их в книге «Символическая логика», изданной в Лондоне в 1881 году. Поэтому такие схемы иногда называют Диаграммы Эйлера — Венна.

Леонард Эйлер (1707 — 1783, Санкт-Петербург, Российская империя) —математик, механик, физик. Адъюнкт по физиологии, профессор физики, профессор высшей математики, внёсший значительный вклад в развитие математики, а также механики, физики, астрономии и ряда прикладных наук.

Эйлер — автор более чем 800 работ по математическому анализу, дифференциальной геометрии, теории чисел, приближённым вычислениям, небесной механике, математической физике, оптике, баллистике, кораблестроению, теории музыки и др.

Почти полжизни провёл в России, где внёс существенный вклад в становление российской науки. В 1726 году он был приглашён работать вСанкт-Петербург, куда переехал годом позже. С 1711 по 1741, а также с 1766 года был академиком Петербургской Академии Наук (в 1741—1766 годах работал в Берлине, оставаясь одновременно почётным членом Петербургской Академии). Хорошо знал русский язык и часть своих сочинений (особенно учебники) публиковал на русском. Первые русские академики-математики (С. К. Котельников) и астрономы (С. Я. Румовский) были учениками Эйлера. Некоторые из его потомков до сих пор живут в России.

Джон Венн (1, английский логик. Работал в области логики классов, где создал особый графический аппарат (так называемые диаграммы Венна), нашедший применение в логико-математической теории «формальных нейронных сетей». Венну принадлежит обоснование обратных операций в логическом исчислении Дж. Буля. Основной областью интереса Джона была логика, и он опубликовал три работы по этой теме. Это были «Логика случая», в которой вводится интерпретация частоты или частотная теория вероятностей в 1866; «Символьная логика», с которой были введены диаграммы Венна в 1881; «Принципы эмпирической логики» в 1889, в которой приводятся обоснования обратных операций в булевой логике.

В математике рисунки в виде кругов, изображающих множества, используются очень давно. Одним из первых, кто пользовался этим методом, был выдающийся немецкий математик и философ (1В его черновых набросках были обнаружены рисунки с такими кругами. Затем этот метод довольно основательно развил и Леонард Эйлер. Он долгие годы работал в Петербургской Академии наук. К этому времени относятся его знаменитые «Письма к немецкой принцессе», написанные в период с 1761 по 1768 год. В некоторых из этих «Писем. » Эйлер как раз и рассказывает о своем методе. После Эйлера этот же метод разрабатывал чешский математик Бернард Больцано (1Только в отличие от Эйлера он рисовал не круговые, а прямоугольные схемы. Методом кругов Эйлера пользовался и немецкий математик Эрнест Шредер (1Этот метод широко используется в книге «Алгебра логики». Но наибольшего расцвета графические методы достигли в сочинениях английского логика Джона Венна (1С наибольшей полнотой этот метод изложен им в книге «Символическая логика», изданной в Лондоне в 1881 году. В честь Венна вместо кругов Эйлера соответствующие рисунки называют иногда диаграммами Венна; в некоторых книгах их называют также диаграммами (или кругами) Эйлера-Венна.

Понятия множества и подмножества используются при определении многих понятий математики и, в частности, при определении геометрической фигуры. Определим как универсальное множество плоскость. Тогда можно дать следующее определение геометрической фигуры в планиметрии:

Геометрической фигурой называется всякое множество точек плоскости. Чтобы наглядно отображать множества и отношения между ними, рисуют геометрические фигуры, которые находятся между собой в этих отношениях. Такие изображения множеств и называют диаграммами Эйлера–Венна. Диаграммы Эйлера–Венна делают наглядными различные утверждения, касающиеся множеств. На них универсальное множество изображают в виде прямоугольника, а его подмножества – кругами. Используется в математике, логике, менеджменте и других прикладных направлениях.

Диаграммы Эйлера-Венна заключается в изображении большого прямоугольника, представляющего универсальное множество U, а внутри его – кругов (или каких-нибудь других замкнутых фигур), представляющих множества. Фигуры должны пересекаться в наиболее общем случае, требуемом в задаче, и должны быть соответствующим образом обозначены. Точки, лежащие внутри различных областей диаграммы, могут рассматриваться как элементы соответствующих множеств. Имея построенную диаграмму, можно заштриховать определенные области для обозначения вновь образованных множеств.

Основные операции над множествами:

Пересечение Объединение Разность

3.Операции над множествами диаграммы Эйлера-Венна

Операции над множествами рассматриваются для получения новых множеств из уже существующих.

Определение. Объединением множеств А и В называется множество, состоящее из всех тех элементов, которые принадлежат хотя бы одному из множеств А, В (рис. 1):

Определение. Пересечением множеств А и В называется множество, состоящее из всех тех и только тех элементов, которые принадлежат одновременно как множеству А, так и множеству В (рис. 2):

Определение. Разностью множеств А и В называется множество всех тех и только тех элементов А, которые не содержатся в В (рис. 3):

Определение. Симметрической разностью множеств А и В называется множество элементов этих множеств, которые принадлежат либо только множеству А, либо только множеству В (рис. 4):

Определение. Абсолютным дополнением множества А называется множество всех тех элементов, которые не принадлежат множеству А (рис. 5):

Теперь более подробно на примерах.

Пусть дана некоторая совокупность предметов, которую после пересчета можно было бы обозначить как

Предположим далее, что часть предметов, 1, 2, 4 и 6, имеет круглую форму, а часть — 2, 3, 4, 8 и 9 — окрашена в белый цвет. В этом случае говорят, что множество V имеет два подмножества

круглых и белых предметов. Можно исходное множество называть фундаментальным, а подмножества A и B – просто множествами.

В результате получим четыре класса элементов:

C0 = — элементы не обладают ни одним из названных свойств,

C1 = — элементы обладают только свойством A (круглые),

C2 = — элементы обладают только свойством B (белые),

C3 = — элементы обладают одновременно двумя свойствами A и B.

На рис. 1.1. указанные классы изображены с помощью диаграммы Эйлера — Венна.

Часто диаграммы не имеют всей полноты общности, например та, что изображена на рис. 1.2. На ней уже множество A полностью включено в B. Для такого случая используется специальный символ включения (Ì): A Ì B = Ì .

Если одновременно выполняются два условия: A Ì B и B Ì A, то A = B, в этом случае говорят, что множества A и B полностью эквивалентны.

После того, как определены четыре класса элементов и даны необходимые сведения о диаграммах Эйлера — Венна, введем операции на множествах. В качестве первой рассмотрим операцию объединения.

a)Объединение

Объединением множеств A = и B =

где È — символ объединения множеств. Таким образом, объединением охватываются три класса элементов — C1, C2 и C3, которые на диаграмме (рис. 1.3) заштрихованы.

Логически операцию объединения двух множеств можно охарактеризовать словами: элемент x принадлежит множеству A или множеству B. При этом связка «или» одновременно означает и связку «и». Факт принадлежности элемента x множеству A обозначается как x Î A. Поэтому то, что x принадлежит A или/и B, выражается формулой:

x Î A È B = (x Î A) Ú (x Î B),

где Ú — символ логической связки или, которая называется дизъюнкцией.

b)Пересечение, дополнение

Пересечением множеств A и B называется множество A Ç B, содержащее те элементы из A и B, которые входят одновременно в оба множества. Для нашего числового примера будем иметь:

Диаграмма Эйлера – Венна для пересечения изображена на рис. 1.4.

То, что x принадлежит одновременно двум множествам A и B можно представить выражением:

x Î A Ç B = (x Î A) Ù (x Î B),

где Ù — символ логической связки «и», которая называется конъюнкцией.

Представим себе операцию, в результате которой окажутся заштрихованными области C1 и C3, образующие множество A (рис. 1.5). Затем еще одну операцию, которая охватит две другие области — C0 и C2, не входящие в A, что обозначается как A (рис.1.6).

Рис. 1.5

Рис. 1.6

Если объединить заштрихованные области на обеих диаграммах, то получим все заштрихованное множество 1; пересечение же A и A даст пустое множество 0, в котором не содержится ни одного элемента:

A È A = 1, A Ç A = 0.

Множество A дополняет множество A до фундаментального множества V (или 1); отсюда название: дополнительное множество A, или дополнение как операция. Дополнение к логической переменной x, т. е. x (не-x), называется чаще всего отрицанием x.

После введения операций пересечения и дополнения все четыре области Ci на диаграмме Эйлера – Венна можно выразить следующим образом:

Путем объединения соответствующих областей Ci можно представить любую множественную операцию, в том числе и само объединение:

A È B = (A Ç B) È (A Ç B) È (A Ç B).

c)Стрелка Пирса, штрих Шеффера и разность

На рис. 1.7 и 1.8 приведены диаграммы двух новых операций, которые называются, соответственно, стрелка Пирса и штрих Шеффера. Эти диаграммы дополняют объединение и пересечение до фундаментального множества V.

Рис. 1.7

Рис. 1.8

На множествах эти операции выглядят следующим образом:

Разностью между множествами A и B называется совокупность тех элементов множества A, которые не вошли во множество B:

Диаграмма Эйлера — Венна для нее приведена на рис. 1.9.

На диаграмме Эйлера — Венна для импликации (рис. 1.10) показано частичное включение множества A во множество B, которое нужно отличать от полного включения (рис. 1.2).

Если утверждается, что «элементы множества A включены во множество B», то область C3 обязательно должна быть заштрихована, а область C1 с такой же необходимостью должна быть оставлена белой. Относительно областей C0 и C1, находящихся в A, заметим, что мы не имеем права оставлять их белыми, но, мы обязаны все же области, попадающие в A, заштриховать.

Е)Симметрическая разность и эквивалентность

Остается привести еще две взаимно дополняющих операции — симметрическую разность и эквивалентность. Симметрическая разность двух множеств A и B есть объединение двух разностей:

Эквивалентность определяется теми элементами множеств A и B, которые для них являются общими. Однако элементы, не входящие ни в A, ни в B, также считаются эквивалентными:

На рис. 1.11 и 1.12 показана штриховка диаграмм Эйлера — Венна.

Рис. 1.11

Рис. 1.12

В заключение отметим, что симметрическая разность имеет несколько названий: строгая дизъюнкция, исключающая альтернатива, сумма по модулю два. Эту операцию можно передать словами — «либо А, либо В», т. е. это логическая связка «или», но без включенной в нее связки «и».

Диаграммы Эйлера-Венна – геометрические представления множеств. Простое построение диаграммы обеспечивает наглядное изображение, представляющее универсальное множество U, а внутри его – кругов (или каких-нибудь других замкнутых фигур), представляющих множества. Фигуры пересекаются в наиболее общем случае, требуемом в задаче, и соответствуют образному изображению. Точки, лежащие внутри различных областей диаграммы, могут рассматриваться как элементы соответствующих множеств. Имея построенную диаграмму, можно заштриховать определенные области для обозначения вновь образованных множеств. Это позволяет нам иметь наиболее полное представление о задаче и ее решении. Простота диаграмм Эйлера-Венна позволяет использовать данный прием в таких направлениях, как математика, логика, менеджмент и других прикладных направлениях.

1. Словарь по логике. — М.: Туманит, изд. центр ВЛАДОС. , . 1997

2. Weisstein, Eric W. «Диаграмма Венна» (англ.) на сайте Wolfram MathWorld.

Видео:Круги Эйлера (диаграммы Венна) - просто и доступно.Скачать

Круги Эйлера — примеры и методы решения логических задач

Видео:Круги Эйлера. Логическая задача на множества. Иностранные языкиСкачать

Множества в математике

Диаграммы Венна помогают показать связь теории множеств и логических операций. Круги Эйлера, множества чисел и других предметов тесно связаны. Под множеством понимается совокупность каких-то объектов, называемых элементами. В множества можно объединять объекты с общим признаком. Например, множество студентов второго курса университета или множество статей, написанных одним учёным. Можно выделить три вида таких математических объектов:

• конечное, например, множество стран;
• бесконечное — множество звёзд во вселенной;
• пустое — множество острых углов в прямоугольнике.

Группа элементов, составляющая множество, входящее в другое, более обширное множество называется подмножеством. Такое отношение получается между множеством действительных чисел и входящим в его состав подмножеством натуральных чисел.

В курсах информатики и обычно изучаются такие темы как «Введение в математическую логику» и «Поиск информации в Интернет». При решении задач по этим темам помощь оказывают диаграммы Венна. Для их построения можно использовать онлайн-калькулятор. Обозначения операций над множествами, которым должны соответствовать обозначения в калькуляторе:

• дополнение ¯A в калькуляторе имеет вид A’;
• пересечение A∩B представлено как A intersection B;
• объединение А⋃B обозначено A union B;
• симметрическая разность A∆B — symmetric difference of A and B;
• Относительное дополнение AB — AB.

Калькулятор выдаёт результат и подробное решение с правильным порядком операций при подстановке конкретных множеств.

Кольцом в теории множеств называют непустую систему R, замкнутую относительно пересечения и симметрической разности, то есть при пересечении или операции симметрической разности любых двух множеств обязательно получается множество, входящее в R. Это означает, что для любых элементов A, B из кольца элементы A∩B и A∆B будут лежать в кольце.

Видео:Математика/3 кл/Петерсон/часть 1/Диаграмма Эйлера-Венна/08.09.21Скачать

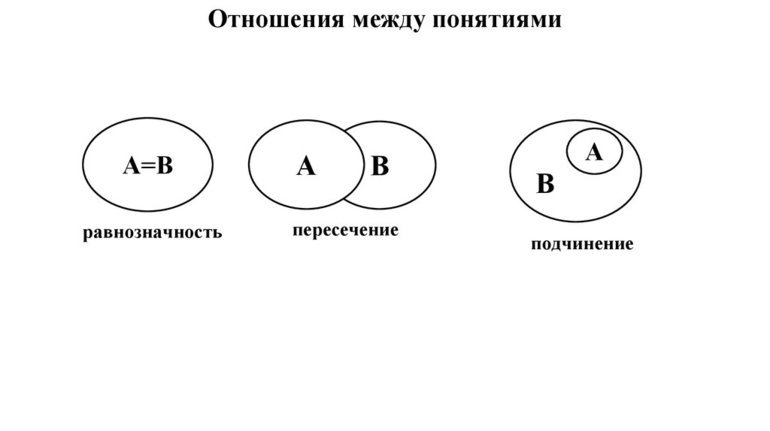
Отношения между понятиями

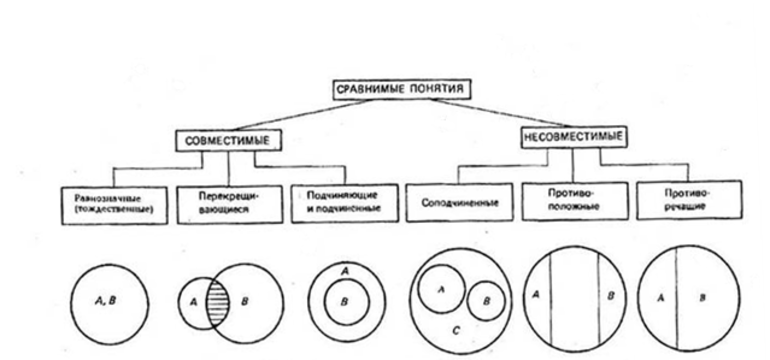
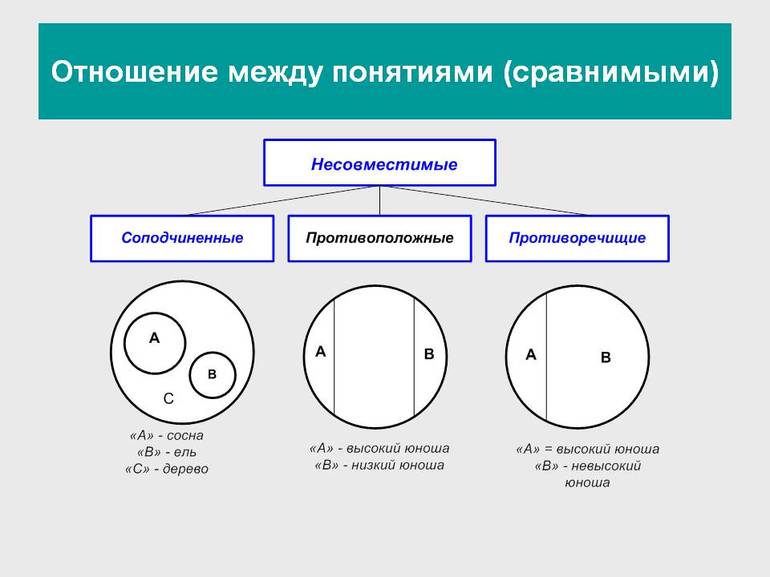
Логические операции, разрешающие доказывать утверждения и делать выводы, основаны на связях и отношениях разных понятий. При классификации понятия делятся на сравнимые, между которыми существуют логические связи и отношения, и несравнимые, которые не имеют связей. К несравнимым относятся, например, «машина» и «квадрат», «озеро» и «клетка». У них нет общих элементов и их нельзя сравнивать.

Рисунок 1

Сравнимые понятия подразделяются на совместимые и несовместимые. Совместимые понятия отличаются тем, что имеют хотя бы один общий элемент:

• равнозначные (тождественные);
• перекрещивающиеся;
• подчиняющие и подчинённые.

У равнозначных понятий объёмы полностью совпадают. Например, А — писатель Чехов, В — автор пьесы «Вишнёвый сад». Графически тождественность можно представить как два круга, слившиеся в один (Рисунок 1).

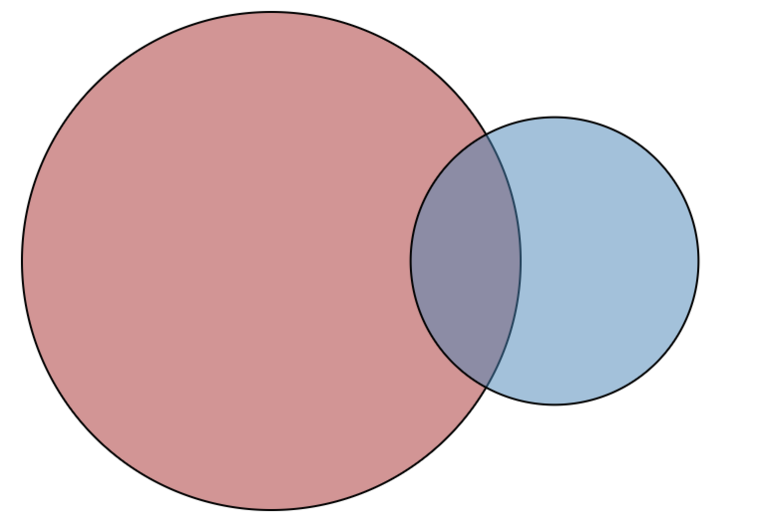
Пересекающимися понятиями, или находящимися в отношении перекрещивания, считаются те, объёмы которых совпадают частично. Пример: A — «математик», B — «репетитор»; A — «студент», B — «спортсмен». Часть объёма понятия «математик» входит в объём понятия «репетитор» и наоборот.

Понятия, состоящие в отношении подчинения, содержат одинаковые элементы, а объём подчинённого целиком входит в объём подчиняющего. Например, «млекопитающее» и «коза».

Несовместимыми называют понятия, не имеющие общих элементов:

• соподчинённые;
• противоположные;
• противоречащие.

Соподчинённые понятия имеют общие элементы и вместе входят в родовое понятие, но в их объёмах общие элементы отсутствуют. Например, А — «корова», B — «овца», C — «млекопитающее». Круги A и B необходимо поместить внутри круга, изображающего объём понятия C, но они не смогут пересекаться, так как не бывает млекопитающих, которые были бы и коровой, и овцой одновременно.

Противоположные понятия — это виды одного и того же рода, но одно из них имеет какой-то признак, а другое не обладает им и содержит признак, несовместимый с первым, направленный против него. Таковы A — «большой дом» и B — «маленький дом». Тут в отличие от отношения противоречия возможны предметы, которые не входят ни в A и ни в B. Если общее родовое C — дом, то в его круге будут изображения двух сегментов A и B, расположенных напротив друг друга, а оставшаяся часть должна соответствовать всем остальным домам (средним, меньше средних).

Противоречащими считается категория понятий, у одного из которых есть какой-то признак, а у другого он отрицается. Например, «чёрный» и «нечёрный», «злой» — «незлой». При этом весь массив родственных элементов делится на две части: одни имеют этот признак, а другие — нет.

Видео:Задача, которую боятсяСкачать

Решение задач, примеры

Круги Эйлера и как решать сложные логические задачи, используя свойства диаграммы, можно показать на примерах.

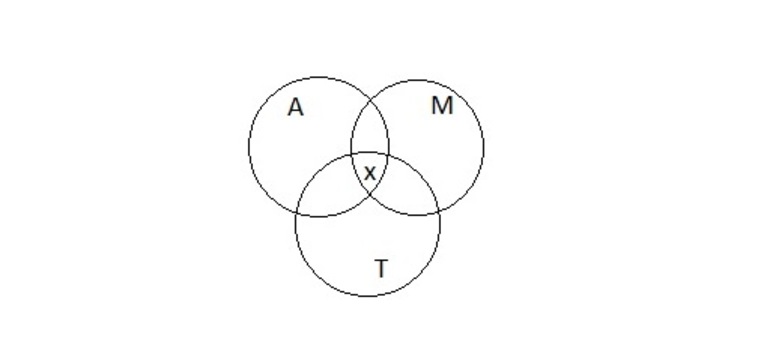
Задача 1. Пусть имеется следующее условие: 54 школьника шестых классов занимаются в авиамодельном, музыкальном и танцевальном кружках. Каждый посещает хотя бы один кружок. Музыкой занимаются 32 ученика, 22 — танцами, 34 — авиамоделированием. Участвуют в музыкальном и танцевальном кружках 11 школьников, в музыкальном и авиамоделировании — 21, в танцевальном и авиамоделировании — 12. Сколько учащихся посещают все три кружка?

Рисунок 2

Проект решения предполагает необходимость расписать всех 54 школьников в соответствии с условиями задачи. Известно, что в авиамодельном кружке 34 ученика. Если прибавить к этому число учеников, которые занимаются музыкой, их 32 человека, то получится A ⋃ M, где ⋃ обозначение объединения множеств, будет состоять из 34 + 32… учеников.

Но при взгляде на круги Эйлера (Рисунок 2) становится понятно, что те, кто занимается и музыкой, и авиамоделированием посчитаны дважды. Это область на диаграмме, которая принадлежит и кругу A, и кругу М, таких учеников 21. Значит, объединение множеств A ⋃ M будет 34 + 32 — 21…

Теперь нужно прибавить 22 школьника, занимающихся танцами. A ⋃ M ⋃ T равно 34 + 32 — 21 + 22… Тут опять некоторые ученики оказываются посчитаны дважды. Можно вычесть из общей суммы тех, кто занимается танцами и музыкой — 11 человек и 12 человек, участвующих в авиамодельном и танцевальном кружках одновременно. Функция принимает следующий вид: A ⋃ M ⋃ T будет 34 + 32 — 21 + 22 — 11 — 12…

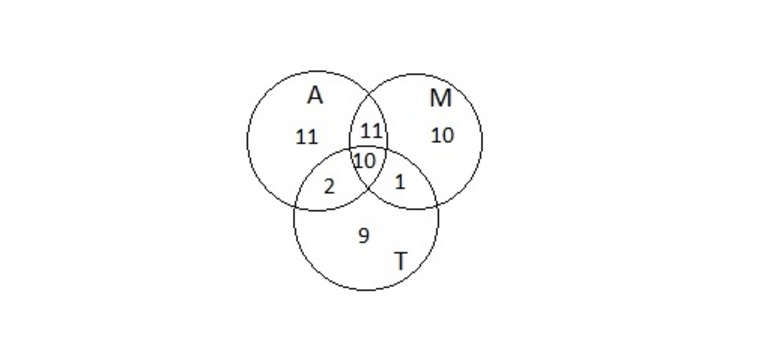
Но при этом школьники, которые посещают все три кружка, оказались отняты дважды. Их число обозначено x и его надо прибавить один раз к имеющейся формуле. Чтобы решить задачу, требуется определить x из полученного уравнения (Рисунок 3).

54 = 34 + 32 — 21 + 22 — 11 — 12 + х; откуда следует, что x = 10. Ответ: 10.

Рисунок 3

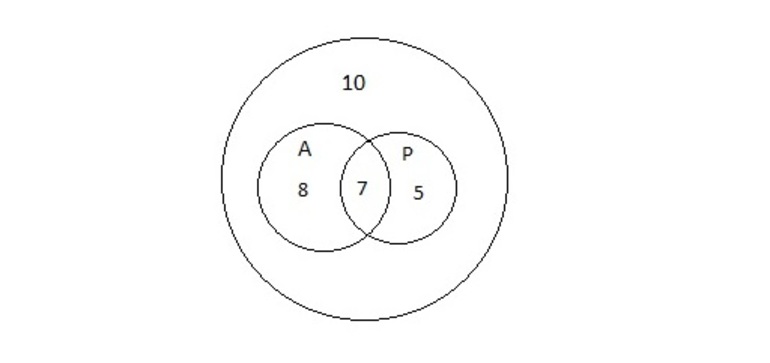
Задача 2. В школьную библиотеку пришло 30 учеников седьмого класса. Из них 15 человек взяли учебник по алгебре, 12 — по русскому языку, 10 человек не взяли ни одного учебника. Сколько учеников получили учебники по алгебре и русскому языку?

Множества на диаграммах представлены на рисунке 4. В большом круге 30 учеников, внутри двух малых 30 — 10 = 20 человек. По условию задачи 15 учеников получили учебник по алгебре, значит, 20 — 15 = 5 учеников получили только учебник по русскому языку. А в условии говорится, что 12 человек взяли учебник по русскому, то есть 12 — 5 = 7 школьников получили учебники и по алгебре, и по русскому. Ответ: 7.

Рисунок 4

Круги Эйлера часто применяются для решения самых разных задач. Они служат для развития способности к логическому мышлению у дошкольников. Большой раздел задач для школьников может решаться с помощью диаграмм. Многие учёные в своих исследованиях тоже обращаются к этому методу, который повышает наглядность решаемых проблем и помогает в их обдумывании. Использование простых фигур позволяет свести решение любой сложной задачи к символической логике и упростить ход рассуждений. Диаграммы могут применяться и в обычной жизни, например при поиске работы. Пересечение кругов «лучше всего получается», «больше всего нравится делать» и «чем можно заработать», возможно, даст нужный результат.

📸 Видео

Самый короткий тест на интеллект Задача Массачусетского профессораСкачать

Множества. Круги Эйлера. Математика 5, 6, 7, 8, 9, 10, 11 класс. Подготовка к ЕГЭ, ОГЭ, ЦТ, экзаменуСкачать

Теория. Числовые множества. Диаграмма Эйлера-Венна (5-11 класс)Скачать

Что такое диаграммы Венна? Душкин объяснитСкачать

Диаграммы Венна и таблицы частот | Графики и диаграммыСкачать

Множество. Элементы множества. 5 класс.Скачать

Множества. Круги ЭйлераСкачать

Диаграмма Венна.Круги ЭйлераСкачать

Диаграммы Эйлера. Решение заданий №17Скачать