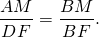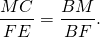Определение медианы
Медиана треугольника — это отрезок, который соединяет вершину треугольника с
серединой противоположной стороны. Медиана делит противолежащую сторону пополам.
Основание медианы — это точка пересечения медианы со стороной треугольника.
На рисунке 1 изображены три медианы, делящие каждая свою противолежащую
сторону пополам. Медианы BF, AH, CE соответственно делят пополам свои
противолежащие стороны AC, CB, AB.
Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Медиана делит площадь треугольника пополам
Медиана делит площадь треугольника пополам
Два треугольника называются равновеликими. Если они имеют одинаковую площадь.
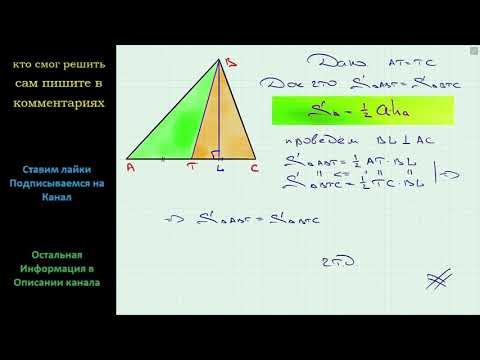
Теорема 1. Медиана делит треугольник на два равновеликих треугольника.
Пусть ВМ – медиана треугольника АВС. Докажем, что

Проведем высоту BH треугольника АВС. Тогда


Так как ВМ – медиана треугольника АВС, то АМ=МС, поэтому



Что и требовалось доказать.
Теорема 2. Медианы треугольника разбивают его на шесть равновеликих треугольников.
Доказательство можно посмотреть, например, в методическом пособии «Опорные задачи по планиметрии».
Из теоремы, в частности следует, что если точку пересечения медиан треугольника соединить со всеми его вершинами, то треугольник разобьется на три равновеликие части.
Задача 1 Две медианы треугольника взаимно перпендикулярны и равны соответственно 3 и 4. Найти площадь треугольника.
Пусть в треугольнике АВС медианы АМ и ВЕ равны 3 и 4 соответственно, 


Так как треугольник АВК прямоугольный с прямым углом ВКА, то 
Так как медиан делят треугольник на 6 равновеликих частей, то 
Задача 2 Медианы треугольника равны 6, 8 и 10, найти площадь треугольника.
Пусть медианы АM, BE и CD данного треугольника соответственно равны 6, 8 и 10, К – точка их пересечения. Отложим на продолжении луча ВЕ за точку Е отрезок EF=KE. Соединим точки С, F и A.
Рассмотрим треугольник KAF.

то

Далее, 

Так как 


Вычислим площадь треугольника AKF:

Теперь сравним площади треугольников AKF и АВС: так как AE – медиана треугольника AKF, то




Отметим, что задачу можно решить по-другому, если воспользоваться тем фактом, что:
площадь треугольника, образованного медианами данного треугольника составляет 
Доказательство можно посмотреть, например, в методическом пособии «Опорные задачи по планиметрии».
Вопросы для самопроверки:
1. Какие треугольники называются равновеликими?
2. Площадь треугольника равна S. Чему равна площадь каждого из треугольников, на которые его разбивает медиана, проведенная к какой-либо стороне этого треугольника?
3. На сколько равновеликих частей разбивают треугольник проведенные в нем три медианы?
4. Площадь треугольника равна S. Цент тяжести этого треугольника соединили с его вершинами. Чему равна площадь каждого из получившихся треугольников?
5. Площадь треугольника равна 48, чему равна площадь треугольника, составленного из медиан этого треугольника?
6. Площадь треугольника, составленного из медиан некоторого треугольника равна 24, чему равна площадь треугольника?
Задачи для самостоятельного решения:
1. Две медианы треугольника взаимно перпендикулярны и равны соответственно 6 и 8. Найти площадь треугольника.
2. Медианы треугольника равны 3, 4 и 5 найти площадь треугольника.
3. Треугольник АВС, стороны которого 13 см, 14 см и 15 см, разбит на три треугольника отрезками, соединяющими точку М пересечения медиан треугольника с вершинами треугольника. Найти площадь треугольника ВМС.
4. Две стороны треугольника равны 10 и 12, а медиана, проведённая к третьей, равна 5. Найдите площадь треугольника.
Видео:Медиана треугольника делит пополам угол ... | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

Медиана делит пополам любой отрезок, параллельный стороне
Медиана, проведённая к стороне треугольника, делит пополам любой отрезок, параллельный этой стороне, с концами на двух других сторонах треугольника.
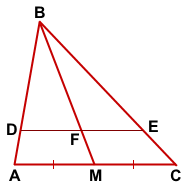
Рассмотрим треугольники ABM и DBF.
У них угол B — общий, ∠BAM=∠BDF (как соответственные при AC||DE и секущей AB).
Следовательно, треугольники ABM и DBF подобны (по двум углам).
Из подобия треугольников следует пропорциональность соответствующих сторон:
Аналогично, треугольники CBM и EBF подобны и
Правые части получившихся равенств равны, приравниваем левые части:
🌟 Видео
Биссектриса прямого угла делит медиану пополам! Найти площадь треугольника.Скачать
Запоминаем: высота, медиана биссектриса треугольникаСкачать

7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

8. Медиана треугольника и её свойства.Скачать

Теорема о точке пересечения медиан треугольника. Доказательство. 8 класс.Скачать

🔥 Свойства МЕДИАНЫ #shortsСкачать

Геометрия Докажите, что медиана треугольника разбивает его на два равновеликих треугольникаСкачать
Построение медианы в треугольникеСкачать

Задача про медиану треугольника. Геометрия 7 класс.Скачать

Точка пересечения медиан в треугольникеСкачать

Все свойства медианы в одной задаче.Скачать

ГЕОМЕТРИЯ 7 класс. Медиана прямоугольного треугольника. Свойство. Доказательство для 7 класса.Скачать

ГЕОМЕТРИЯ 8 класс. Свойство медиан треугольникаСкачать

Все факты о медиане треугольника для ЕГЭСкачать

Свойство биссектрисы треугольника с доказательствомСкачать

Доказать, что медиана, проведенная к гипотенузе, равна половине гипотенузыСкачать

Медиана в прямоугольном треугольникеСкачать

3 свойства биссектрисы #shortsСкачать