Даны три отрезка построй треугольник (3 видео)

351 Постройте треугольник по двум сторонам и высоте к третьей стороне.

Даны три отрезка M₁N₁, M₂N₂, M₃N₃ (рис. 148, а). Требуется построить такой треугольник ABC, у которого две стороны, скажем АВ и АС, равны соответственно данным отрезкам M₁N₁ и M₂N₂, а высота АН равна отрезку M₃N₃. Проведем решение задачи по описанной схеме.

Допустим, что искомый треугольник ABC построен (рис. 148, б). Мы видим, что сторона АВ и высота АН являются гипотенузой и катетом прямоугольного треугольника АВН. Поэтому построение треугольника ABC можно провести по такому плану: сначала построить прямоугольный треугольник АВН, а затем достроить его до всего треугольника ABC. Построение

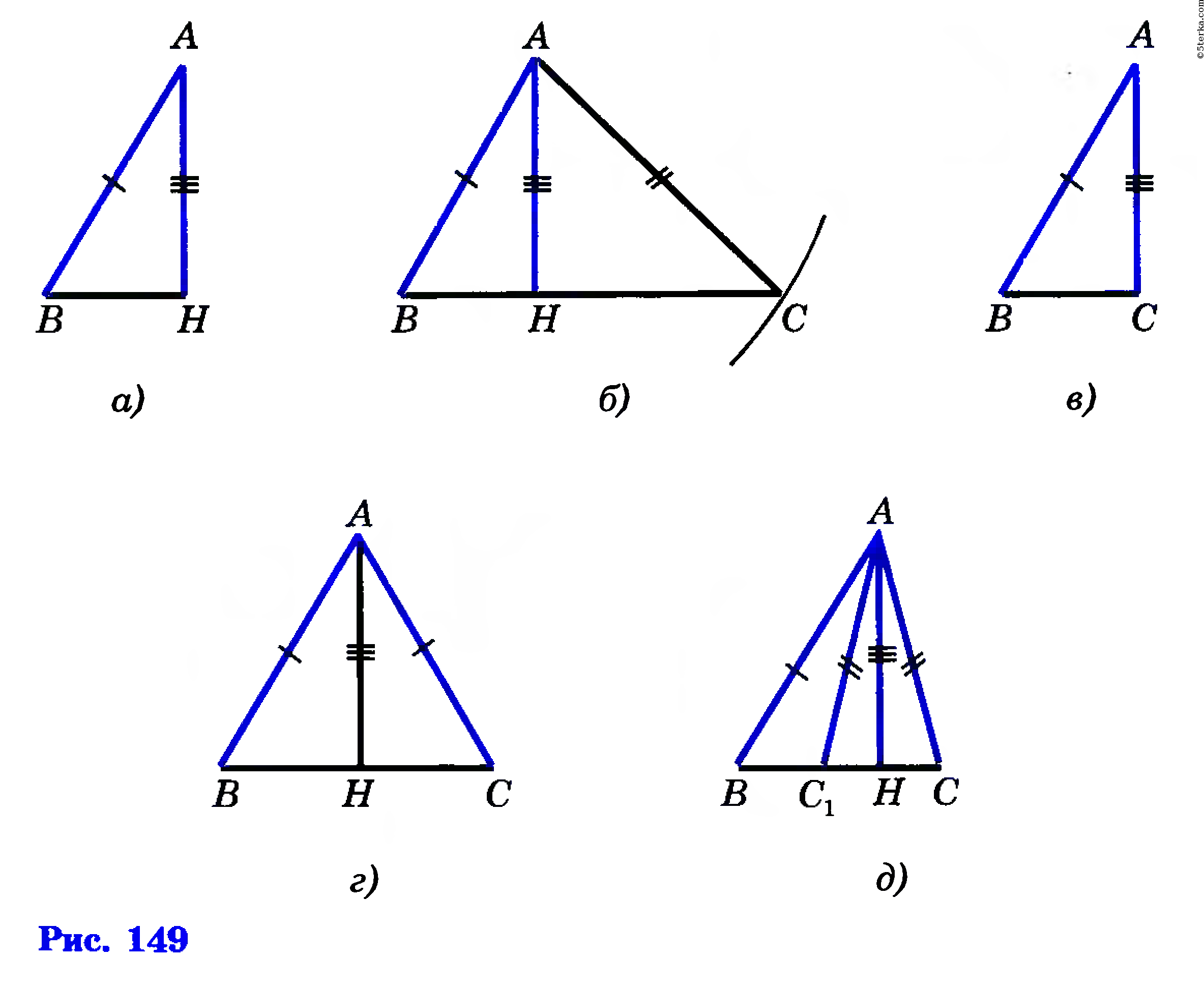
Строим прямоугольный треугольник АВН, у которого гипотенуза АВ равна отрезку M₁N₁, а катет АН равен данному отрезку M₃N₃. Как это сделать, мы знаем (задача 314, в). На рисунке 149, а изображен построенный треугольник АВН. Затем проводим окружность радиуса M₂N₂ с центром в точке А. Одну из точек пересечения этой окружности с прямой ВН обозначим буквой С. Проведя отрезки ВС и АС, получим искомый треугольник ABC (рис. 149, б).

Треугольник ABC действительно искомый, так как по построению сторона АВ равна M₁N₁, сторона АС равна M₂N₂, а высота АН равна M₃N₃, т. е. треугольник ABC удовлетворяет всем условиям задачи. Исследование

Нетрудно сообразить, что задача имеет решение не при любых данных отрезках M₁N₁, M₂N₂, М₃N₃. В самом деле, если хотя бы один из отрезков M₁N₁ и M₂N₂ меньше M₃N₃, то задача не имеет решения, так

как наклонные АВ и АС не могут быть меньше перпендикуляра АН. Задача не имеет решения и в том случае, когда M₁N₁=M₂N₂=M₃N₃ (объясните почему). В остальных случаях задача имеет решение. Если М₁N₁>М₃N₃, а M₂N₂=M₃N₃, то задача имеет единственное решение: в этом случае сторона АС совпадает с высотой АН и искомый треугольник является прямоугольным (рис. 149, в). Если М₁N₁>М₃N₃, а M₂N₂=M₁N₁ то задача также имеет единственное решение: в этом случае треугольник ABC равнобедренный (рис. 149, г). И наконец, если M₂N₂>M₃N₃ и М₁N₁≠М₂N₂, то задача имеет два решения — треугольники ABC и АВС₁ на рисунке 149, д.

Решебник по геометрии за 7 класс (Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев, Э.Г.Позняк, И.И.Юдина, 2012 год),
задача №351
к главе «Задачи на построение».

Содержание

задание, нужно записать на языке паскаль: Даны три отрезка, можно ли из них построить треугольник?
Построение треугольника по трём сторонам
Построение
Отрезок равный отрезку b
Отрезок равный отрезку c
Доказательство
📺 Видео

Видео:Даны три отрезка имеющие длины a, b, c. Постройте отрезок длиной икс используя циркуль и линейкуСкачать

задание, нужно записать на языке паскаль: Даны три отрезка, можно ли из них построить треугольник?

var
a, b, c: real;
begin
write (‘стороны? ‘);
readln (a,b,c);
write(‘треугольник’);
if (a >= b + c) or (b >= a + c) or (c >= a + b) then write(‘ не’);
writeln (‘ существует’);
end.

Если сумма двух каждых больше третьего то можно

Смотри. В теории треугольник можно построить, если самая большая сторона меньше чем сумма двух других меньше. Кусочек кода
var a,b,c:integer; //Твои переменные, где значение длины отрезков

write(‘Введите три длины отрезков’);

if (a>b and a>c) then

if (a a and b>c) then

if (b a and c>b) then

Видео:Построение угла равного данномуСкачать

Построение треугольника по трём сторонам

Даны три отрезка a, b и c. И требуется построить треугольник со сторонами , равными данным отрезкам.

Видео:Строим треугольник по трем сторонам (Задача 5).Скачать

Построение

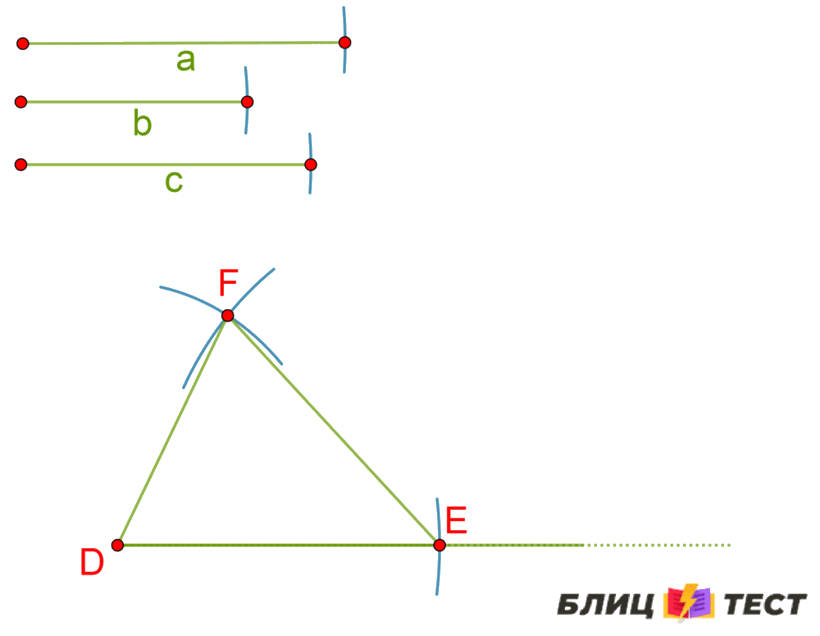
Для выполнения задачи построим равный первому отрезок о двух концах, и от одного конца отложим отрезок равный второму, и от другого конца отложим отрезок равный третьему.

Построение треугольника по трём сторонам

Отрезок равный отрезку а

Построим произвольный луч с началом в точке D — первый луч. Замерим циркулем отрезок a и тем же раствором циркуля отложим на первом луче от его начала отрезок DE равный отрезку a.

Отрезок равный отрезку b

Замерим циркулем отрезок b и тем же раствором циркуля построим вторую вспомогательную дугу окружности с центром в точке D.

Отрезок равный отрезку c

Замерим циркулем отрезок c и тем же раствором циркуля построим третью вспомогательную дугу окружности с центром в точке E — так чтобы третья дуга пересекала вторую дугу. Получилась точка пересечения F. Соединим точку F с точками D и E — получился требуемый треугольник.

Доказательство

У полученного треугольника сторона DE равна отрезку a, сторона DF равна отрезку b (потому что точка F лежит на окружности с центром в точке D и с радиусом b) и сторона EF равна отрезку c (потому что точка F лежит на окружности с центром в точке E и с радиусом c). Построение закончено.