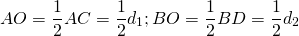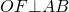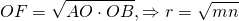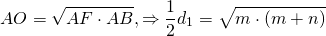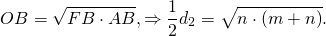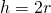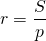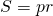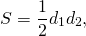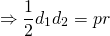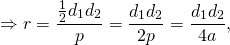Дано abcd ромб r вписанной окружности 5 fo перпендикулярно abc

Нахождение радиуса вписанной в ромб окружности

В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить радиус окружности, вписанной в ромб. Также разберем примеры решения задач для закрепления изложенного материала.

Формулы вычисления радиуса вписанной в ромб окружности

Через диагонали и сторону

Радиус r вписанной в ромб окружности равняется произведению его диагоналей, деленному на сторону, умноженную на 4.

• d₁ и d₂ – диагонали ромба;
• a – сторона ромба.

Через диагонали

Радиус r вписанной в ромб окружности можно найти, зная только длины его обеих диагоналей:

Эту формулу можно получить, если сторону a в формуле выше выразить через диагонали (согласно одному из свойств ромба):

Через сторону и угол

Радиус окружности r, вписанной в ромб, равняется половине произведения его стороны и синуса любого угла.

Через высоту

Радиус вписанного в ромб круга равняется половине его высоты.

Примеры задач

Задание 1
Известно, что диагонали ромба равны 6 и 8 см. Найдите радиус окружности, вписанной в него.

Решение
Применим соответствующую формулу, подставив в нее известные значения:

Задание 2
Вычислите радиус вписанного в ромб круга, если его сторона равна 11 см, а один из углов – 30°.

Решение
В данном случае мы можем воспользоваться последней из рассмотренных выше формул:

Площадь ромба – формула, пример расчет, как начертить

Через диагонали

Диагональ ромба d₁Диагональ ромба d₂Результат

Признаки ромба

∠BAC = ∠CAD или ∠BDA = ∠BDC

Δ ABO = Δ BCO = Δ CDO = Δ ADO

Свойства ромба

На рисунке выше ( ABCD ) – ромб, ( AC = DB = CD = AD ) . Так как ромб – это параллелограмм, то он обладает всеми свойствами параллелограмма, но так же есть свойства присущие только ромбу.

В любой ромб можно вписать окружность. Центр окружности, вписанной в ромб, является точкой пересечения его диагоналей. Радиус окружности равен половине высоты ромба:

Формула вычисления площади

1. По длине стороны и высоте:

Площадь ромба (S) равняется произведению длины его стороны и высоты, проведенной к ней:

S = a*h

2. По длине стороны и углу

Площадь ромба равняется произведению квадрата длины его стороны и синуса угла между сторонами:

S = a 2 *sin α

3. По длинам диагоналей

Площадь ромба равна одной второй произведения его диагоналей.

Основные свойства ромба

∠BAC = ∠CAD, ∠ABD = ∠DBC, ∠BCA = ∠ACD, ∠ADB = ∠BDC

AC 2 + BD 2 = 4AB 2

Примеры задач

Задание 1
Найдите площадь ромба, если длина его стороны равна 10 см, а высота, проведенная к ней – 8 см.

Решение:
Используем первую формулу, рассмотренную выше: S = 10 см * 8 см = 80 см 2 .

Задание 2
Найдите площадь ромба, сторона которого равняется 6 см, а острый угол – 30°.

Решение:
Применим вторую формулу, в которой используются известные по условиям задания величины: S = (6 см) 2 * sin 30° = 36 см 2 * 1/2 = 18 см 2 .

Задание 3
Найдите площадь ромба, если его диагоналей равны 4 и 8 см, соответственно.

Решение:
Воспользуемся третьей формулой, в которой используются длины диагоналей: S = 1/2 * 4 см * 8 см = 16 см 2 .

Через основание и высоту

Высоты ромба hСторона ромба а

Площади фигур

Расчет площади квадрата, прямоугольника, параллелограмма, треугольника, трапеции, ромба, круга (площадь фигур).Площади фигур

Площадь ромба по углу и противолежащей диагонали

Площадь ромба по углу и диагонали проведенной из этого угла

Способ расчета площади ромба

Ромб – это параллелограмм, у которого все стороны равны. Ромб у которого все углы прямые называется квадратом.
Формула площади ромба: ,
где a – стороны, h – высота

Ромб – это параллелограмм, у которого все стороны равны. Ромб у которого все углы прямые называется квадратом.
Формула площади ромба: ,
где d1, d2 – диагонали

Ромб – это параллелограмм, у которого все стороны равны. Ромб у которого все углы прямые называется квадратом.
Формула площади ромба: ,
где a – сторона, α – угол между сторонами

Ромб – это параллелограмм, у которого все стороны равны. Ромб у которого все углы прямые называется квадратом.
Формула площади ромба:
где r – радиус вписанной окружности, α – угол между сторонами

Ромб – это параллелограмм, у которого все стороны равны. Ромб у которого все углы прямые называется квадратом.
Формула площади ромба: ,
где r – радиус вписанной окружности, a – сторона

Формула площади ромба через две стороны и угол между ними

a — сторона ромба;

— любой угол ромба.

Найти площадь ромба, если каждая из его сторон равна 10 см, а угол между двумя смежными сторонами равен 30 градусам.

Решение

По формуле получаем:

S = a 2 ⋅ sin ( α ) = 1 0 0 ⋅ sin ( 3 0 ∘ ) = 5 0 (см. кв.)

Ответ: 50 см. кв.

Формула площади ромба через угол и радиус вписанной окружности

Формула площади ромба через сторону и угол

Таблица с формулами площади ромба

В зависимости от известных исходных данных, площадь ромба можно вычислить по различным формулам.

исходные данные (активная ссылка для перехода к калькулятору)	эскиз	формула
1	сторона и высота
2	диагонали
3	диагональ и угол между сторонами
4	диагональ и угол между сторонами
5	сторона и угол между сторонами
6	радиус вписанной окружности и угол между сторонами
7	сторона и радиус вписанной окружности

Периметр ромба

Периметром ромба называется сумма длин всех сторон ромба.
Длину стороны ромба можно найти за формулами указанными выше.

Узнать ещё

Знание — сила. Познавательная информация

В ромб вписана окружность

Когда в условии задачи сказано, что в ромб вписана окружность, в ходе ее решения может быть использовано одно из следующих рассуждений.

Точка касания вписанной в ромб окружности делит его сторону на отрезки

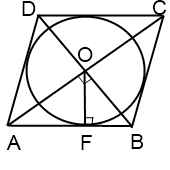
В этом случае радиус ромба и его диагонали можно найти, используя соотношения в прямоугольном треугольнике.

Например, F — точка касания вписанной в ромб окружности — делит сторону AB на отрезки AF=m, FB=n. О — центр вписанной в ромб окружности — является точкой пересечения его диагоналей. Треугольник AOB — прямоугольный (так как диагонали ромба взаимно перпендикулярны).

— как радиус, проведенный в точку касания. Значит, OF — высота, проведенная к гипотенузе. Отсюда

Высота ромба через радиус вписанной окружности

Радиус вписанной в ромб окружности

Радиус вписанной окружности можно найти по формуле

S — площадь ромба, p — его полупериметр (p=2a, где a — сторона ромба).

Соответственно, площадь ромба через радиус вписанной в него окружности

Поскольку площадь ромба также равна

Площадь ромба через отрезки, на которые делит сторону ромба точка касания вписанной в него окружности, может быть найдена как

Решение задач по теме «Перпендикулярность прямых и плоскостей»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов

Сертификат и скидка на обучение каждому участнику

Геометрия, 10 класс

Тема. Решение задач по теме «Перпендикулярность прямых и плоскостей»

Тип урока. Урок систематизации и обобщения знаний

Цель. Сформировать навык решения задач по изученной теме.

Задачи. Образовательные– систематизировать, закрепить вопросы теории и отработать,расширить навыки решения основных типов задач по теме «Перпендикулярность плоскостей», создать условия контроля усвоения знаний и умений.

Развивающие– развивать пространственное воображение, способствовать формированию умений применять приемы сравнения, обобщения, выявления главного, переноса знаний в новую ситуацию, развитию математического кругозора, мышления и речи; побуждать к самоконтролю и взаимоконтролю.

Воспитательные– поддерживать интерес к предмету, воспитывать познавательную активность, способствовать формированию коммуникативной компетентности.

Требования к знаниям, умениям и навыкам.

Знать: теоремы о перпендикулярностях прямых в пространстве, перпендикулярности прямой и плоскости, теорему о трех перпендикулярах.

Уметь: применять названные теоремы при решении стереометрических задач.

Оборудование: карточки с заданиями, учебник.

2.Актуализация опорных знаний

2. Решение задач по готовым чертежам

Ответ. 13

Ответ. 17

3. Решение задач.

1. Длина стороны ромба ABCD равна 8 см, длина диагонали BD равна 12 см. Через точку О пересечения диагоналей ромба проведена прямая ОК, перпендикулярная его плоскости. Найдите расстояние от точки К до вершин ромба, если ОК = 14 см.

2. Длины сторон треугольника ABC соответственно равны: ВС = 10 см, АВ = 8 см, АС = 4 см. Через сторону АС проведена плоскость а, составляющая с плоскостью данного треугольника угол 30°. Найдите расстояние от вершины В до плоскости α.

5. Самостоятельная работа

ответ.13

ответ. 13

ответ.48

2. Дано: ABCD – прямоугольник, АB = , FC  ( ABC ),
Р FAB = 30°. Найдите расстояние от точки F до прямой AB .

ответ 6

Домашняя работа. Повторить изученный материал, реш. 194, доп. Задача 3 на карточке

Найдите расстояние от точки F до прямой AB .

ответ. 13

ответ.48

2. Дано: ABCD – прямоугольник, АB = , FC  ( ABC ),
Р FAB = 30°. Найдите расстояние от точки F до прямой AB .

ответ 6

Ответ. 13

Ответ. 17

3. Решение задач.

1. Длина стороны ромба ABCD равна 8 см, длина диагонали BD равна 12 см. Через точку О пересечения диагоналей ромба проведена прямая ОК, перпендикулярная его плоскости. Найдите расстояние от точки К до вершин ромба, если ОК = 14 см.

2. Длины сторон треугольника ABC соответственно равны: ВС = 10 см, АВ = 8 см, АС = 4 см. Через сторону АС проведена плоскость а, составляющая с плоскостью данного треугольника угол 30°. Найдите расстояние от вершины В до плоскости α.

Ответ. 13

Ответ. 17

1. Длина стороны ромба ABCD равна 8 см, длина диагонали BD равна 12 см. Через точку О пересечения диагоналей ромба проведена прямая ОК, перпендикулярная его плоскости. Найдите расстояние от точки К до вершин ромба, если ОК = 14 см.

2. Длины сторон треугольника ABC соответственно равны: ВС = 10 см, АВ = 8 см, АС = 4 см. Через сторону АС проведена плоскость а, составляющая с плоскостью данного треугольника угол 30°. Найдите расстояние от вершины В до плоскости α.

Урок геометрии по теме «Перпендикулярность прямой и плоскости». 10-й класс

Разделы: Математика

Класс: 10

Цели:

1. закрепить вопросы теории по теме «Перпендикулярность прямой и плоскости»;
2. вырабатывать навыки применения теоретических знаний к решению типовых задач на перпендикулярность прямой и плоскости.

План:

1. Теоретический опрос.
   1. Доказательство изученных теорем у доски.
   2. Фронтальный опрос.
   3. Презентации учащихся по данной теме.
2. Решение задач.
   1. Решение устных задач по готовым чертежам.
   2. Решение письменных задач (по группам).
   3. Самостоятельная работа с индивидуальным заданием.
3. Итог урока. Задание на дом.

Ход урока

I. Теоретический опрос (4 ученика у доски)

1) доказать лемму о 2-ух параллельных прямых, одна из которых перпендикулярна к третьей;
2) доказать теорему о 2-ух параллельных прямых, одна из которых перпендикулярна к плоскости;
3) доказать обратную теорему о параллельности 2-ух прямых, перпендикулярных к плоскости;
4) доказать признак перпендикулярности прямой и плоскости.

Пока ученики готовятся у доски к ответу, с классом проводится фронтальный опрос.
(С помощью мультимедиапроектора на экране появляются вопросы (Приложение 1), и ученики отвечают на них)

1. Закончить предложение:

а) две прямые в пространстве называются перпендикулярными, если… (угол между ними равен 90°)
б) прямая называется перпендикулярной к плоскости, если… (она перпендикулярна к любой прямой, лежащей в этой плоскости)
в) если две прямые перпендикулярны к плоскости, то они… (параллельны)
г) если плоскость перпендикулярна к одной из двух параллельных прямых, то она… (перпендикулярна и к другой прямой)
д) если две плоскости перпендикулярны к одной прямой, то они… (параллельны)

2. Дан параллелепипед

б) Определите взаимное расположение:
1) прямой CC₁ и плоскости (DСВ) (ответ: они перпендикулярны)
2) прямой D₁C₁ и плоскости (DCB) (ответ: они параллельны)

Далее выслушиваются ответы учеников у доски с дополнениями и исправлениями по необходимости. Затем рассматриваются презентации по данной теме, подготовленные рядом учеников в качестве зачётных работ (Приложение 2, Приложение 3, Приложение 4).
(Накануне изучения каждой темы учащимся предлагается такой вариант зачёта)

II. Решение задач.

1. Решение задач по готовым чертежам (Устно)

№1

Дано: ∆ ABC — прямоугольный; AM ⊥ AC; M ∉ (ABC)
Доказать: AC ⊥ (AMB)
Доказательство: Т.к. AC ⊥ AB и AC ⊥ AM, а AM ⋂ AB, т.е. АМ и АВ лежат в плоскости (АМВ), то AC ⊥ (AMB) по признаку перпендикулярности прямой и плоскости.
Ч.т.д.

№2

Дано: ВМDC — прямоугольник, M ∉ (ABC), MB ⊥ AB
Доказать: CD ⊥ (ABC)
Доказательство: MB ⊥ BC, т.к. ВМDC – прямоугольник, MB ⊥ AB по условию, BC ⋂ AB, т.е. ВС и АВ лежат в плоскости (АВС) ⇒ MB ⊥ (ABC) по признаку перпендикулярности прямой и плоскости. СD ∥ МВ по свойству сторон прямоугольника ⇒ CD ⊥ (ABC) по теореме о двух параллельных прямых, одна из которых перпендикулярна к плоскости (то и другая прямая перпендикулярна к этой плоскости).
Ч.т.д.

№3

Дано: АВСD – прямоугольник, M ∉ (ABC), MB ⊥ BC
Доказать: AD ⊥ AM
Доказательство:
1) ∠ABC = 90°, т.к. АВСD – прямоугольник ⇒ BC ⊥ AB, BS ⊥ MB по условию, MB ⋂ AB = B, т.е. МВ и АВ лежат в плоскости (АМВ) ⇒ BC ⊥ (AMB) по признаку перпендикулярности прямой и плоскости.
2) BC ∥ AD (по свойству сторон прямоугольника) ⇒ AD ⊥ (AMB) по теореме о двух параллельных прямых, одна из которых перпендикулярна плоскости (то и другая прямая перпендикулярна к этой плоскости).
3) Т.к. AD ⊥ (AMB) ⇒ AD ⊥ AM по определению прямой, перпендикулярной плоскости.
Ч.т.д.

№4

Дано: АВСD – параллелограмм, M ∉ (ABC), МВ = МD, МА = МС
Доказать: MO ⊥ (ABC)
Доказательство:
1) Т.к. О – точка пересечения диагоналей параллелограмма, то АО = СО и ВО = DO. ∆ BMD — равнобедренный, т. к. ВМ = МD по условию, значит МО — медиана и высота, т.е. MO ⊥ BD.
2) Аналогично доказывается в ∆ AMC: MO ⊥ AC.
3) Итак, MO ⊥ BD и MO ⊥ AC. а ВD и АС – пересекающиеся прямые, лежащие в плоскости (АВС) ⇒ MO ⊥ (ABC) по признаку перпендикулярности прямой и плоскости.
Ч.т.д.

(Устные ответы к каждой задаче требуется обосновывать, проговаривая всякий раз формулировки применяемых теорем)

2. Решение письменных задач

Класс делится на три группы (например, по рядам), и каждой группе даётся задача с последующей проверкой решения у доски.

№1.2 (№125 учебника)

Через точки P и Q прямой РQ проведены прямые, перпендикулярные к плоскости α и пересекающие её соответственно в точках P₁ и Q₁. Найдите P₁Q₁, если PQ = 15 cм; PP₁ = 21,5 cм; QQ₁ = 33,5 cм.
Решение:

1) PP₁ ⊥ α и QQ₁ ⊥ α по условию ⇒ PP₁ ∥ QQ₁ (обосновать);
2) PP₁ и QQ₁ определяют некоторую плоскость β, α ⋂ β = P₁Q₁;
3) PP₁Q₁Q — трапеция с основаниями PP₁ и QQ₁, проведём PK ∥ P₁Q₁;
4) QK = 33,5 — 21,5 = 12 (см)

P1Q1 = PK =

= 9 см.

№2.2

1) ∆ ABD: ∠BAD = 90°; АD = BC = 8 см;

ВD =

см;

2) ∆ DD₁B: ∠D₁DB = 90°;

DD1 =

= 12 см;

3) SBB1D1D = BD ∙ DD1 =

см 2 .

Ответ:

см 2 .

№3.2

Отрезок МН пересекает плоскость α в точке К. Из концов отрезка проведены прямые МЕ и НР, перпендикулярные к плоскости α. НР = 4 см; МЕ = 12 см; НК = 5 см. Найдите отрезок РЕ.
Решение:

1) Т.к. прямые МЕ и НР перпендикулярны к плоскости α, то МЕ ∥ НР (обосновать) и через них проходит некоторая плоскость β. α ⋂ β = EP;
2)МЕ ⊥ EP; НР ⊥ EP(обосновать), т.е. ∠MEK = ∠HPK = 90°;

3) ∆ HPK: KP =

= 3 см;

4) ∠EMK = ∠PHK (накрест лежащие для параллельных прямых МЕ и НР и секущей МН),

тогда ∆ MEK ∆ HPK по двум углам и

; т.е.

⇒ EK =

= 9 см,

РЕ = РК + КЕ, РЕ = 3 + 9 = 12 см.

Ответ: РЕ = 12 см.

3. Самостоятельная работа (направлена на проверку усвоения материала по данной теме)

1) AA₁ ⊥ AB, AA₁ ⊥ AD, а AB ⋂ AD = A ⇒ AA₁ ⋂ (ABC) (по признаку перпендикулярности прямой и плоскости), а т.к. AA₁ ∥ BB₁, то BB₁ ⊥ (ABC) ⇒ BB₁ ⊥ BD;
2) ∆ ABD: ∠BAD = 90°. По теореме Пифагора:

Вариант I	Вариант II
Через вершины А и В прямоугольника АВСD проведены параллельные прямые AA1 и BB1, не лежащие в плоскости прямоугольника. Известно, что AA1 ⊥ AB, AA1 ⊥ AD. Найдите B1B, если B1D = 25 см, AB = 12 см, AD = 16 см.	Через вершины А и В ромба АВСD проведены параллельные прямые AA1 и BB1, не лежащие в плоскости ромба. Известно, что BB1 ⊥ BC, BB1 ⊥ AB. Найдите A1A, если A1C = 13 см, BD = 16 см, AB = 10 см.

BD =

= 20 см;

3) ∆ B₁BD – прямоугольный. По теореме Пифагора:

B1B =

= 15 см.

1) BB₁ ⊥ AB, BB₁ ⊥ BC, а AB ⋂ BC = B ⇒ BB₁ ⋂ (ABC) (по признаку перпендикулярности прямой и плоскости), а т.к. BB₁ ∥ AA₁, то AA₁ ⊥ (ABC) ⇒ AA₁ ⊥ AC;
2) Используя свойство диагоналей ромба, имеем в ∆ AOB: ∠AOB = 90°, BO = ½ BD = 8 см. По теореме Пифагора:

AO =

= 6 см,

AO = ½ AC ⇒ AC = 12 см;
3) ∆ A₁AC – прямоугольный. По теореме Пифагора:

AA1 =

= 5 см.

Индивидуальное задание для более сильных учеников. (Вариант III)

1) Т.к. CD ⊥ (FDC) ⇒ CD ⊥ AC и CD ⊥ BC, т.е. ∆ ADC, ∆ BDC – прямоугольные;
2) ∆ ADC = ∆ BDC (по двум катетам) ⇒ AD = BD, т.е. ∆ ADB – равнобедренный и DM – медиана, а значит и высота; 3) DC ⊥ MC ⇒ MCD – прямоугольный,

тогда MC =

= 9;

4) ∆ ABC – равносторонний, поэтому СМ – медиана и высота, т.е. ∆ MCB – прямоугольный, ∠B = 60°,

sin ∠B =

, тогда

,

а АВ = ВС (по условию).
5) S_{∆ ADB} = ½ DM ∙ AB;

S∆ ADB = ½ ∙ 15 ∙

.

Ответ:

III. Подводятся итоги урока. Задание на дом: повторить теоретический материал по изученной теме, глава II, №130, №131.

Для подготовки к уроку использовались материалы учебника «Геометрия – 10-11» авторов Л.С. Атанасяна, В.Ф. Бутузова и др., методические рекомендации к учебнику «Изучение геометрии в 10-11 классах» авторов С.М. Саакяна, В.Ф. Бутузова, «Поурочные разработки по геометрии» автора В.А. Яровенко.