Видео:№640. Даны окружность с центром О радиуса 4,5 см и точка А. Через точку А проведены две касательныеСкачать
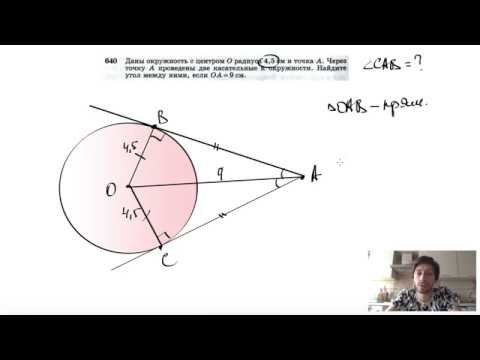
Ваш ответ
Видео:Окружность, диаметр, хорда геометрия 7 классСкачать
решение вопроса
Видео:№649. Начертите окружность с центром О и отметьте на ней точку А. Постройте хорду АВ так, чтобы:Скачать
Похожие вопросы
- Все категории
- экономические 43,282
- гуманитарные 33,619
- юридические 17,900
- школьный раздел 607,049
- разное 16,829
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Видео:Геометрия 8 класс (Урок№28 - Свойства хорд окружности.)Скачать
Постройте хорду данной окружности, равную и параллельную заданному отрезку.
Докажем сначала, что геометрическое место середин хорд окружности, равных данному отрезку, меньшему диаметра, — окружность, концентрическая данной.
Пусть a — данный отрезок, R — радиус данной окружности с центром O. Построим прямоугольный треугольник по гипотенузе (радиус данной окружности R) и катету (половина данного отрезка a). Радиусом, равным второму катету построенного прямоугольного треугольника, проведём окружность, концентрическую данной. Через произвольную точку M построенной окружности проведём к ней касательную. Пусть A и B — точки её пересечения с данной окружностью. Тогда OM 
AB, поэтому M — середина AB, а т.к. хорды, равноудаленные от центра окружности, равны, то AB = a.
Обратно, пусть M — середина хорды AB данной окружности и AB = a. Тогда OM — катет прямоугольного треугольника OMA, в котором OA = R и AM = 
a. Следовательно, точка M лежит на построенной окружности.
Отсюда вытекает следующее построение. Строим произвольную хорду данной окружности с центром O, равную данному отрезку. Радиусом, равным расстоянию от центра данной окружности до этой хорды, проводим окружность с центром O. Через точку O проводим прямую, перпендикулярную данному отрезку. Через точки пересечения этой прямой с построенной окружностью, проводим прямые, параллельные данному отрезку.
Если данный отрезок меньше диаметра окружности, то задача имеет два решения. Если данный отрезок равен диаметру окружности, то задача имеет единственное решение. Если данный отрезок больше диаметра окружности, то задача не имеет решений.
Предположим, что искомая хорда AB построена. Пусть MN — данный отрезок. Тогда при параллельном переносе на вектор 
(или 
) точка A перейдёт в точку B, а данная окружность S — в окружность S1, проходящую через точку B.
Отсюда вытекает следующий способ построения. Строим образ S1 данной окружности при параллельном переносе на вектор 
(или 
). Точки пересечения окружностей S и S1 — концы искомых хорд.
Если окружности S1 и S не пересекаются, то задача не имеет решений.
Видео:Определение центра дуги окружности, построение окружности по 3 точкамСкачать
Всё про окружность и круг
Окружность — это геометрическое место точек плоскости, равноудаленных от некоторой заданной точки (центра окружности). Расстояние между любой точкой окружности и ее центром называется радиусом окружности (радиус обозначают буквой R).
Значит, окружность — это линия на плоскости, каждая точка которой расположена на одинаковом расстоянии от центра окружности.
Кругом называется часть плоскости, ограниченная окружностью и включающая ее центр.
Отрезок, соединяющий две точки окружности, называется хордой. Хорда, проходящая через центр окружности, представляет собой диаметр. Диаметр окружности равен ее удвоенному радиусу: D = 2R.
Точка пересечения двух хорд делит каждую хорду на отрезки, произведение которых одинаково: a1a2 = b1b2
Касательная к окружности всегда перпендикулярна радиусу, проведенному в точку касания.
Отрезки касательных к окружности, проведенные из одной точки, равны: AB = AC, центр окружности лежит на биссектрисе угла BAC.
Квадрат касательной равен произведению секущей на ее внешнюю часть
Центральный угол — это угол, вершина которого совпадает с центром окружности.
Дугой называется часть окружности, заключенная между двумя точками.
Мерой дуги (в градусах или радианах) является центральный угол, опирающийся на данную дугу.
Вписанный угол это угол, вершина которого лежит на окружности, а cтороны угла пересекают ее.
Вписанный угол равен половине центрального, если оба угла опираются на одну и ту же дугу окружности.
Внутренние углы, опирающиеся на одну и ту же дугу, равны.
Сектором круга называется геометрическая фигура, ограниченная двумя радиусами и дугой, на которую опираются данные радиусы.
Периметр сектора: P = s + 2R.
Площадь сектора: S = Rs/2 = ПR 2 а/360°.
Сегментом круга называется геометрическая фигура, ограниченная хордой и стягиваемой ею дугой.
📺 Видео
Касательные к окружности с центром O в точках A и B ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать
Всё про углы в окружности. Геометрия | МатематикаСкачать
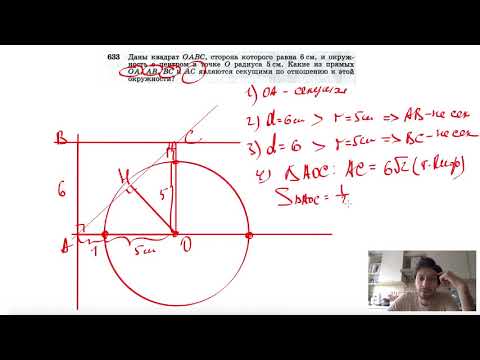
№633. Даны квадрат ОАВС, сторона которого равна 6 см, и окружность с центром в точке О радиуса 5 см.Скачать
№150. Даны окружность, точка А, не лежащая на ней, и отрезок PQ. Постройте точку М на окр-тиСкачать
№ 150 - Геометрия 7-9 класс АтанасянСкачать
№634. Радиус ОМ окружности с центром О делит хорду АВ пополам. Докажите, что касательнаяСкачать
№145. Отрезок МК — диаметр окружности с центром О, а МР и РК — равные хорды этой окружностиСкачать
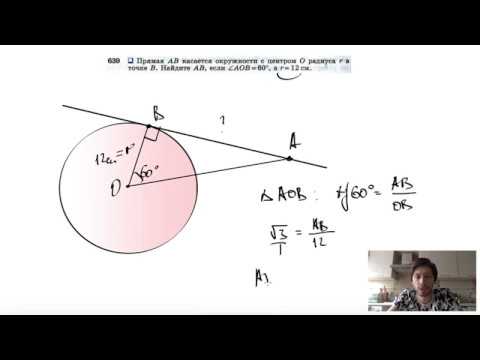
№639. Прямая АВ касается окружности с центром О радиуса r в точке В. Найдите АВСкачать
Построить описанную окружность (Задача 1)Скачать
Найти центр и радиус окружностиСкачать
Окружность вписанная в треугольник и описанная около треугольника.Скачать
№ 147 - Геометрия 7-9 класс АтанасянСкачать
Окружность. 7 класс.Скачать
№149. Даны прямая а, точка В, не лежащая на ней, и отрезок PQ. Постройте точку М на прямой a такСкачать
Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать
