Дан треугольник серединный перпендикуляр

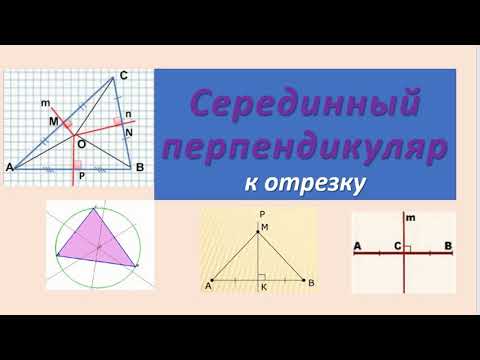
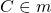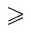Что такое серединный перпендикуляр к отрезку? Что можно сказать о пересечении серединных перпендикуляров к сторонам треугольника? К сторонам многоугольника?

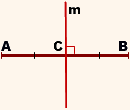
Серединный перпендикуляр к отрезку — это прямая, перпендикулярная данному отрезку и проходящая через его середину.

m — серединный перпендикуляр к отрезку AB, если

точка C — середина отрезка AB,

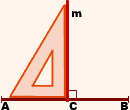
Чтобы построить серединный перпендикуляр к данному отрезку с помощью угольника, нужно:

1) найти середину отрезка;

2) провести через эту точку прямую, перпендикулярную данному отрезку (для этого угольник прикладываем прямым углом к середине отрезка так, чтобы она сторона угольника проходила через отрезок, а через другую сторону проводим прямую):

Свойства серединного перпендикуляра.

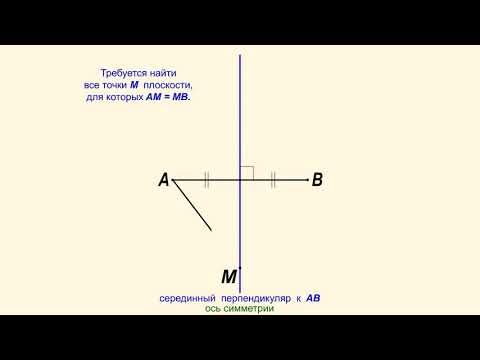
1) Геометрическое место точек, равноудаленных от двух данных точек, есть серединный перпендикуляр к отрезку, соединяющему эти точки.

Например, прямая m — геометрическое место точек, равноудаленных от точек A и B (рисунок 1).

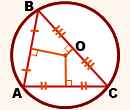
2) Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке. Эта точка является центром описанной около треугольника окружности.

3) Если около многоугольника можно описать окружность, то центр этой описанной окружности является точкой пересечения серединных перпендикуляров к сторонам многоугольника.

Видео:Серединный перпендикулярСкачать

Задание №16 ЕГЭ (профильный уровень)

В прямоугольный треугольник АВС с прямым углом А

и катетами АВ = 3; АС = 5 вписан квадрат ADEF.
а) Докажите, что треугольники BDE и EFC подобны.
б) Найдите отношение площади треугольника EFC к площади квадрата ADEF.

2. Вневписанная в треугольник АВС окружность касается его боковой стороны и продолжения основания АС.

а) Докажите, что радиус этой окружности равен высоте ВН треугольника АВС.

б) Найдите площадь треугольника АВС, если радиус окружности равен 8, а АС·АВ = 120.

3. Две окружности касаются внешним образом в точке L. Прямая AB касается первой окружности в точке A, а второй — в точке B. Прямая BK пересекает первую окружность в точке D, прямая AK пересекает вторую окружность в точке C.

а) Докажите, что прямые AD и BC параллельны.

б) Найдите площадь треугольника ALB, если известно, что радиусы окружностей равны 8 и 2.

4. В треугольник ABC вписана окружность радиуса R, касающаяся стороны AC в точке D, причём AD= r.

а) Докажите, что треугольник ABC прямоугольный.

б) Вписанная окружность касается сторон AB и BC в точках M и N. Найдите площадь треугольника BMN, если известно, что r= 1 и CD =3.

5. Дан треугольник АВС. Серединный перпендикуляр к стороне АВ пересекается с биссектрисой угла ВАС в точке К, лежащей на стороне ВС.

а) Докажите, что АС2 =ВС·СК.

б) Найдите радиус окружности, вписанной в треугольник АКС, если sinВ = 0,8 и сторона АС= 30.

Видео:Урок 12. Серединный перпендикуляр к отрезку (7 класс)Скачать

Задачи на построение циркулем и линейкой с примерами решения

Содержание:

Основные задачи на построение циркулем и линейкой:

В данном параграфе рассмотрим вопрос о построении геометрических фигур. Вы уже знаете, что геометрические построения можно осуществлять с помощью масштабной линейки, циркуля, транспортира и чертежного угольника. В то же время оказывается, что многие геометрические фигуры можно построить, пользуясь только циркулем и линейкой без масштабных делений.

При построении геометрических фигур с помощью циркуля и линейки без масштабных делений учитывается, что:

1. с помощью линейки можно провести произвольную прямую, а также построить прямую, проходящую через две точки;
2. с помощью циркуля можно провести окружность произвольного радиуса, а также построить окружность с центром в данной точке и радиусом, равным данному отрезку.

Теперь рассмотрим основные задачи на построение циркулем и линейкой: построение угла, равного данному, построение серединного перпендикуляра к отрезку, построение биссектрисы угла.

Видео:Высота, биссектриса, медиана. 7 класс.Скачать

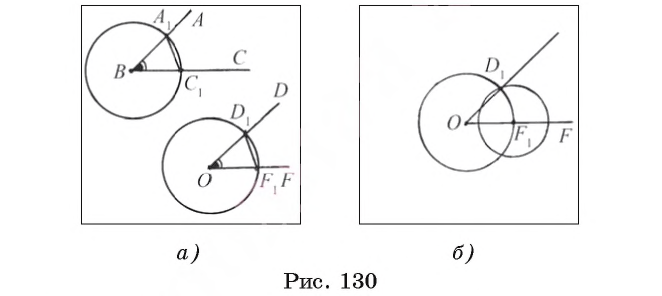
Задача 1 (построение угла, равного данному)

От данного луча OF отложите угол, равный данному углу ABC.

Предположим, что угол DOF, удовлетворяющий условию задачи, построен (рис. 130, а).

Пусть

1) Строим окружность 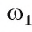(В, R) , где R — произвольный радиус, и отмечаем точки А₁ и С₁ пересечения ее со сторонами угла ABC.

2) Строим окружность 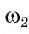(0, R) с центром в точке О того же радиуса R и отмечаем ее точку пересечения F₁ с лучом OF.

3) Строим окружность (F₁, A₁C₁).

4) Пусть D₁ — одна из точек пересечения окружностей 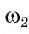(0, R) и (F₁, A₁C₁) (рис. 130, б). Тогда угол D₁OF — искомый. Докажем, что D₁OF =ABC.

Равенство D₁OF =ABC следует из равенства треугольников А₁ВС₁ и D₁OF₁. Действительно, по построению А₁В = D₁O = С₁В = F₁O. Кроме того, по построению F₁D₁ = А₁С₁, следовательно, треугольники А₁ВС₁ и D₁OF₁ равны по трем сторонам. Отсюда следует, что D₁OF =А₁ВС₁, т. е. построенный угол D₁OF равен данному углу ABC.

Видео:Геометрия 8 класс (Урок№30 - Свойство серединного перпендикуляра.)Скачать

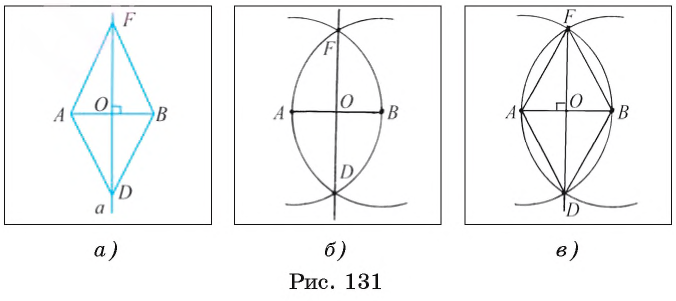
Задача 2 (построение серединного перпендикуляра к отрезку)

Постройте серединный перпендикуляр к данному отрезку АВ.

Проведем рассуждения, которые помогут осуществить необходимое построение. Предположим, что серединный перпендикуляр а к отрезку АВ построен (рис. 131, а). Пусть точки F и D лежат на серединном перпендикуляре так, что OF = OD. Прямоугольные треугольники FOB и DOB равны по двум катетам, следовательно, BF = BD. Иначе говоря, точки F и D лежат на окружности (B, BF) и BF > ОВ. Аналогично AF =AD, так как треугольник FOA равен треугольнику DOA. Кроме того, легко увидеть, что AF = BF. Таким образом, точки F и D лежат также и на окружности (A, BF).

1) Строим окружности (A, R) и (B, R) , где R AВ. Пусть, например, R = AB: (A, AB) и (B, AB) (рис. 131, б).

2) Отмечаем точки F и D пересечения окружностей (A, AB) и (B, AB).

3) Тогда прямая FD — серединный перпендикуляр к отрезку АВ. Докажем это.

Рассмотрим треугольники FAD и FBD (рис. 131, в). Указанные треугольники равны по трем сторонам. Следовательно, AFD = BFD. Отсюда следует, что в равнобедренном треугольнике AFD отрезок FO является биссектрисой, а значит, и высотой и медианой, т. е. прямая FO — серединный перпендикуляр к отрезку АВ.

Видео:Построение серединных перпендикуляров треугольника с помощью циркуляСкачать

Задача 3 (построение биссектрисы угла)

Постройте биссектрису данного угла ABC.

Допустим, что биссектриса BE данного угла ABC построена (рис. 132, а). Пусть точки F и D лежат на сторонах угла так, что BF = BD, О = FD BE, а точка Т лежит на луче, противоположном лучу ОВ. Из равенства прямоугольных треугольников FOT и DOT (FO = OD, катет ОТ — общий) следует, что FT = DT, т. е. точка Т принадлежит окружностям равных радиусов с центрами в точках F и D. Построив точку Т, мы построим биссектрису ВТ данного угла.

1) Строим окружность (B, R₁) произвольного радиуса R₁ с центром в вершине В данного угла (рис. 132, б).

2) Отмечаем точки F и D, в которых окружность (B, R) пересекает соответственно стороны ВА и ВС данного угла.

3) Строим окружности (F, R₂) и (D, R₂), где R2 > FD. Отмечаем точку Т их пересечения, которая лежит внутри данного угла.

4) Проводим луч ВТ. Луч ВТ — искомый. Докажем это.

Рассмотрим треугольники BFT и BDT (рис. 132, в). Эти треугольники равны по трем сторонам (BF = BD и FT = DT — по построению, ВТ — общая сторона). Из равенства этих треугольников следует, что FBT = DBT, т. е. луч ВТ — биссектриса угла ABC.

Видео:Наклонная, проекция, перпендикуляр. 7 класс.Скачать

Построение треугольника по трем элементам

В данном пункте рассмотрим задачи на построение треугольника по: а) двум сторонам, и углу между ними; б) стороне и двум прилежащим к ней углам; в) трем сторонам.

Видео:8 класс, 36 урок, Свойства серединного перпендикуляра к отрезкуСкачать

Задача 4 (построение треугольника по двум сторонам и углу между ними)

Постройте треугольник, две стороны которого равны двум данным отрезкам а и b, а угол между этими сторонами равен данному углу hk.

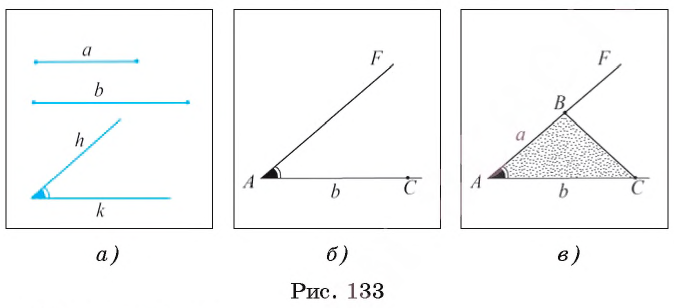
Даны два отрезка а, b и угол hk (рис. 133, а). Требуется с помощью циркуля и линейки построить треугольник ABC, две стороны которого, например, АВ и АС, равны соответственно отрезкам а и b, а угол ВАС равен углу hk.

1) Проведем прямую, на ней отложим отрезок АС, равный отрезку b (рис. 133, б).

2) Строим угол CAF, равный углу hk.

3) На луче AF отложим отрезок АВ, равный отрезку а, и проведем отрезок ВС. Треугольник ABC — искомый (рис. 133, в).

По построению имеем, что АС = b, АВ = а и BAC = hk.

При любых данных отрезках а и b и неразвернутом угле hk каждое из построений 1) — 3) выполнимо, т. е. искомый треугольник можно построить. Треугольники, которые удовлетворяют условию задачи и строятся при различном выборе прямой и отрезка АС, равны между собой по двум сторонам и углу между ними, поэтому говорят, что данная за дача имеет единственное решение.

Видео:Серединный перпендикуляр. 7 класс геометрия. Центр описанной окружности треугольникаСкачать

Задача 5 (построение треугольника по стороне и двум прилежащим к ней углам)

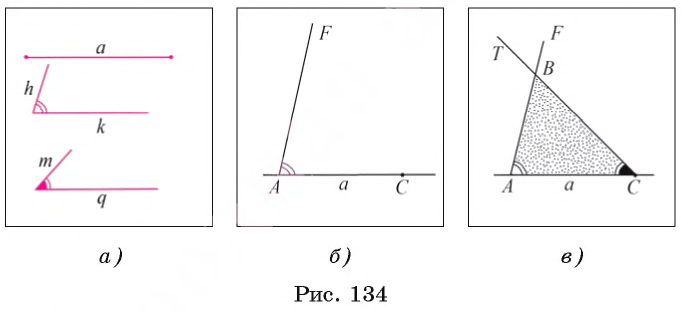
Постройте треугольник, сторона которого равна данному отрезку а, а углы, прилежащие к этой стороне, равны данным углам hk и mq.

Дан отрезок а и два угла hk и mq (рис. 134, а). Требуется с помощью циркуля и линейки построить треугольник ABC, сторона которого, например АС, равна отрезку а, а углы ВАС и ВСА равны соответственно углам hk и mq.

1) Проведем прямую и на ней отложим с помощью циркуля отрезок АС, равный отрезку а (рис. 134, б).

2) Строим угол CAF, равный углу hk.

3) Строим угол ACT, равный углу mq.

4) Отмечаем точку В пересечения лучей AF и СТ. Треугольник ABC — искомый (рис. 134, в).

По построению имеем, что АС = a, BAC = hk и ACB = mq.

Для любого данного отрезка а и неразвернутых углов hk и mq каждое из построений 1) — 4) выполнимо, т. е. искомый треугольник можно построить. Треугольники, которые удовлетворяют условию задачи и строятся при различном выборе прямой и отрезка АС, равны между собой по стороне и двум прилежащим к ней углам, поэтому говорят, что данная задача имеет единственное решение.

Видео:ЕГЭ 2024 по математике. №1,17 Медиана, биссектриса, высота, серединный перпендикулярСкачать

Задача 6 (построение треугольника по трем сторонам)

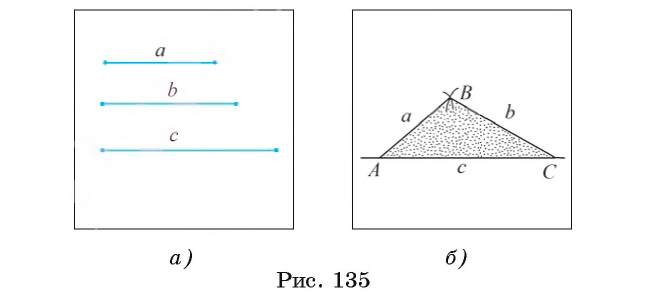
Постройте треугольник, стороны которого равны данным отрезкам а, b, с.

Даны отрезки а, b, с (рис. 135, а). Требуется с помощью циркуля и линейки построить треугольник ABC, стороны которого АВ, ВС и АС равны соответственно отрезкам a, b и с.

1) Проведем прямую и на ней с помощью циркуля отложим отрезок АС, равный отрезку с (рис. 135, б).

2) Строим окружность (A, a).

3) Строим окружность (C, b).

4) Пусть В — одна из точек пересечения окружностей (A, a) и (C, b). Тогда треугольник ABC — искомый.

По построению АС = с, АВ = а, ВС = b.

Данная задача не всегда имеет решение. Известно, что в любом треугольнике длина каждой стороны меньше суммы длин двух других его сторон. Таким образом, если длина какого-либо из данных отрезков больше суммы длин двух других, то нельзя построить треугольник, стороны которого равны данным отрезкам.

• Задачи на построение по геометрии
• Угол — определение, виды, как обозначают с примерами
• Перпендикулярные прямые в геометрии
• Признаки равенства треугольников
• Соотношения между сторонами и углами треугольника
• Неравенство треугольника — определение и вычисление
• Свойства прямоугольного треугольника
• Расстояние между параллельными прямыми

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

📹 Видео

Построение медианы в треугольникеСкачать

Построение высоты в треугольникеСкачать

Свойства и признаки равнобедренного треугольника Серединный перпендикулярСкачать

Геометрия 7 класс (Урок№11 - Перпендикуляр к прямой.)Скачать

75. Свойства серединного перпендикуляра к отрезкуСкачать

7 класс, 16 урок, Перпендикуляр к прямойСкачать

Серединный перпендикуляр и второй признак равенства треугольников. Геометрия 7 классСкачать

Средняя линия треугольника и трапеции. 8 класс.Скачать

Построение угла, равного данному. 7 класс.Скачать

Построение серединных перпендикуляров треугольника с помощью подручных средствСкачать

№258. Из середины D стороны ВС равностороннего треугольника ABC проведен перпендикулярСкачать