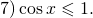Cosx меньше 0 на окружности

Знание — сила. Познавательная информация

Видео:Решить неравенство cosСкачать

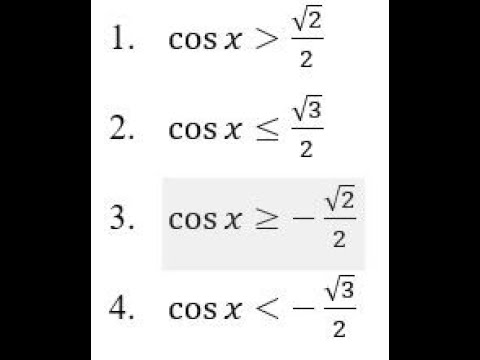
cosx меньше a

Рассмотрим решение тригонометрических неравенств вида cosx меньше a (cosx

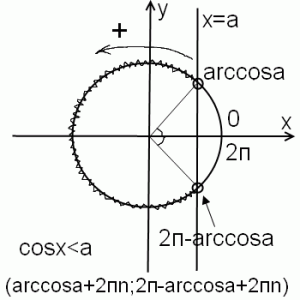
Снова применяем ассоциацию косинус-колобок. Оба кругленькие, оба начинаются с ко-. Колобку, в силу особенности его фигуры, удобнее двигаться влево-вправо, а не вверх-вниз. Влево-вправо на координатной плоскости — движение по оси ox. Значит, косинус — это x. То есть абсцисса, координата x точки на окружности. Геометрически cosx=a в точках пересечения единичной окружности и прямой x=a (прямая, параллельная оси ox). Соответственно, точки окружности, находящиеся правее этой прямой, соответствуют значениям косинуса, большим a, а cosx меньше a — левее этой прямой. Прямая и окружность могут пересекаться, не пересекаться и касаться. От их взаимного расположения зависит решение тригонометрического неравенства cosx меньше a.

Первая точка пересечения прямой и окружности находится, как обычно, — это arccos a. Поскольку нам нужны значения, в которых cos x меньше a, из первой точки ко второй мы идем по верхнему пути, против часовой стрелки. При таком направлении обхода угол увеличивается. Вторую точку получили, немного не дойдя до 2п. На сколько не дошли? На тот же угол, который соответствует arccos a. Раз не дошли, то это число вычитаем из 2п. Поэтому вторая точка пересечения прямой с окружностью есть 2п-arccos a. Итак, решением неравенства cos x меньше a является промежуток (arccos a; 2п-arccos a). Поскольку период косинуса равен 2п, к каждому из концов промежутка прибавляем 2пn, где n -целое число (то есть n принадлежит Z). Получаем окончательный вариант ответа: (arccos a+2пn; 2п-arccos a+2пn). Для нестрогого неравенства точки закрашиваем и ставим квадратные скобки.

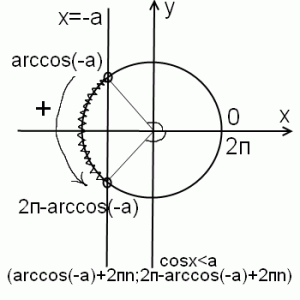
2) cos x меньше -a, при 0

Решение неравенства аналогично первому случаю. Отличие — нужно вычислить арккосинус отрицательного числа (чуть позже я расскажу, как легко запомнить значения arccos (-a) с помощью ассоциации). А пока что arccos (-a)= п-arccos a. Ко второй точке здесь тоже идем против часовой стрелки, то есть значение угла увеличивается. Не доходим до 2п на величину arccos(-a), отсюда вторая точка есть 2п-arccos(-a). Чтобы учесть все решения неравенства, к концам промежутка прибавляем 2пn. Если неравенство нестрогое, точки закрашиваем и включаем в ответ (с квадратной скобкой).

3) cosx 1.

При таких a окружность целиком расположена правее прямой x=-a и нет ни одного x, удовлетворяющего требованию cosx меньше -a. Поэтому решений нет.

В этом случае точку пересечения окружности и прямой исключать из решения не нужно, значит, x — любое число и решением является вся числовая прямая: (-∞;+∞).

Единственным решением этого тригонометрического неравенства является точка п. С учетом периодичности косинуса, решением является множество точек вида п+2пn, где n — целое число.

И в заключении — пример решения тригонометрического неравенства вида cosx меньше a: cosx Светлана Иванова, 07 Окт 2012

Видео:Как решать тригонометрические неравенства?Скачать

Простейшие тригонометрические неравенства

п.1. Решение неравенств с синусом

Алгоритм решения неравенства (sinxgt a)

Шаг 1. В числовой окружности на оси синусов отметить точку с ординатой (a). Провести горизонталь (y=a), отметить точки её пересечения с окружностью.

Шаг 2. Решить уравнение (sin⁡x=a). Про решение простейших тригонометрических уравнений – см. §19 данного справочника. Полученные базовые решения являются значениями точек пересечения, подписать их.

Шаг 3. Дуга числовой окружности над проведенной горизонталью – искомое решение. Записать ответ, обходя дугу против часовой стрелки. Добавить к концам полученного интервала полный период.
Решение имеет вид: ((arcsina+2pi k; pi-arcsin a+2pi k))

$$ sin xgt frac12 $$ 1. Проводим горизонталь (y=frac12), отмечаем точки пересечения (незакрашенные, т.к. неравенство строгое). 2. Решаем уравнение (sinx=frac12) begin x=(-1)^kfracpi6+pi k= left[ begin fracpi6+2pi k\ frac+2pi k end right. end Подписываем точку справа (fracpi6) и точку слева (frac). 3. При обходе полученной дуги против часовой стрелки получаем интервал: ((fracpi6; frac)). Добавляем к концам интервала полный период. Ответ: (left(fracpi6;+2pi k; frac+2pi kright))

Алгоритм решения неравенства (sinxgeq a) будет таким же, только точки на числовой окружности будут закрашенными, и в ответе будет отрезок (с квадратными скобками).

Алгоритм решения неравенства (sin⁡xlt a) будет отличаться тем, что в ответе нужно записывать дугу под горизонталью (y=a). При этом не забываем, что дугу нужно обходить в сторону возрастания. Поэтому угол слева пишут отрицательным (отсчитывая период назад).

Наконец, в неравенстве (sin⁡xleq a) всё будет то же, что и в (sin⁡xlt a). Только точки на концах будут закрашенными и войдут в ответ (с квадратными скобками).

$$ sin xleq -frac<sqrt> $$ 1. Проводим горизонталь (y=-frac<sqrt>), отмечаем точки пересечения (закрашенные, т.к. неравенство нестрогое). 2. Решаем уравнение (sinx=-frac<sqrt>) begin x=(-1)^kleft(-fracpi4right)+pi k= left[ begin -frac+2pi k\ -frac+2pi k end right. end Подписываем точку справа (-frac) и точку слева (-frac). 3. При обходе полученной дуги против часовой стрелки получаем отрезок: (left[-frac;-fracright]). Добавляем к концам отрезка полный период. Ответ: (left[-frac+2pi k;-frac+2pi kright])

п.2. Решение неравенств с косинусом

Алгоритм решения неравенства (cosxgt a)

Шаг 1. В числовой окружности на оси косинусов отметить точку с абсциссой (a). Провести вертикаль (x=a), отметить точки её пересечения с окружностью.

Шаг 2. Решить уравнение (cos⁡x=a). Полученные базовые решения являются значениями точек пересечения, подписать их.

Шаг 3. Дуга числовой окружности справа от проведенной вертикали – искомое решение. Записать ответ, обходя дугу против часовой стрелки. Добавить к концам полученного интервала полный период.
Решение имеет вид: ((-arccos⁡a+2pi k; arccos⁡a+2pi k))

$$ cosxgt frac<sqrt> $$ 1. Проводим вертикаль (x=frac<sqrt>), отмечаем точки пересечения (незакрашенные, т.к. неравенство строгое). 2. Решаем уравнение (cosx=frac<sqrt>) begin x=pmfracpi6+2pi k end Подписываем точку снизу (-fracpi6) и точку сверху (frac). 3. При обходе полученной дуги против часовой стрелки получаем интервал: (left(-fracpi6;fracpi6right)). Добавляем к концам интервала полный период. Ответ: (left(-fracpi6;+2pi k; frac+2pi kright))

Алгоритм решения неравенства (cosxgeq a) будет таким же, только точки на числовой окружности будут закрашенными, и в ответе будет отрезок (с квадратными скобками).

Алгоритм решения неравенства (cosxlt a) будет отличаться тем, что в ответе нужно записывать дугу слева от вертикали (x=a). При этом не забываем, что дугу нужно обходить в сторону возрастания, сверху вниз. Значение угла снизу должно быть больше, чем угла сверху.

Наконец, в неравенстве (cos⁡xleq a) всё будет то же, что и в (cosxlt a). Только точки на концах будут закрашенными и войдут в ответ (с квадратными скобками).

п.3. Решение неравенств с тангенсом

Алгоритм решения неравенства (tgxgt a)

Шаг 1. На оси тангенсов (касательной к числовой окружности в точке (1,0)) отметить точку с ординатой (a). Провести луч из начала координат через отмеченную точку, отметить точку её пересечения с окружностью.

Шаг 2. Решить уравнение (tg⁡x=a). Полученное базовое решение является значением точки пересечения.

Шаг 3. Дуга числовой окружности от отмеченной точки до (fracpi2) (в которой (tgxrightarrow +infty)) – искомое решение. Записать ответ, обходя дугу против часовой стрелки. Добавить к концам полученного интервала полный период.
Решение имеет вид: (left(arctga+pi k; fracpi2+pi kright))

$$ tg xgt -frac<sqrt> $$ 1. На оси тангенсов отмечаем точку (-frac<sqrt>). Проводим луч из начала координат через эту точку. 2. Решаем уравнение (tgx=-frac<sqrt>) begin x=-fracpi6+pi k end Подписываем точку снизу (-fracpi6.) Верхней границей интервала будет (fracpi2), угол, в котором (tgxrightarrow +infty .) 3. При обходе полученной дуги против часовой стрелки получаем интервал: (left(-fracpi6;fracpi2right)). Добавляем к концам интервала период для тангенса. Строго говоря, на числовой окружности длиной (2pi) получим две дуги для тангенса с периодом (pi). Ответ: (left(-fracpi6;+pi k; frac+pi kright))

Алгоритм решения неравенства (tg⁡xlt a) будет отличаться тем, что в ответе нужно записывать дугу от точки (-fracpi2) (в которой (tgxrightarrow -infty)) до найденного арктангенса.

Для нестрогих неравенств будут получаться полуинтервалы, в которых точки (pmfracpi2) ((tgxrightarrow pminfty)) будут ограничены круглой скобкой, а найденные арктангенсы – квадратной.

п.4. Решение неравенств с котангенсом

Решение неравенств с котангенсом аналогично решению с тангенсом. Для решения используется ось котангенсов (касательная к числовой окружности в точке (0;1)).

В неравенствах вида (ctgxgt a) пределу (ctgxrightarrow +infty) соответствует угол 0.

В неравенствах вида (ctgxlt a) пределу (ctgxrightarrow -infty) соответствует угол (pi).

п.5. Примеры

Пример 1. Решите неравенства:

a) (sinxleq frac<sqrt>) $$ xinleft[-frac+2pi k; frac+2pi kright] $$	б) (cosxlt -frac) $$ xinleft(frac+2pi k; frac+2pi kright) $$
в) (sinxgt -frac<sqrt>) $$ xinleft(-frac+2pi k; frac+2pi kright] $$	г) (tgxgeq 1) $$ xinleft.left(-frac+pi k; frac+pi kright.right] $$

Пример 2*. Решите неравенства:

a) (cosxgt -1) Справа от вертикали (x=-1) расположена вся числовая окружность, кроме точки (pi).

Ответ: (xne pi+2pi k)б) (4cos^2frac x2-3leq 0)
(4cdot fracleq 3)
(2+2cosxleq 3)
(cosxleqfrac12)

Ответ: (left[fracpi3+2pi k; frac+2pi kright])

в) (-sqrtlt tgxleq 5)
(-arctgsqrt+pi klt xleq arctg5+pi k)
(-fracpi3+pi klt xleq arctg5+pi k)
Ответ: (left.left(-frac+pi k; arctg5+pi kright.right])

г) (tgleft(x-fracpi4right)gtsqrt)
(arctgsqrt+pi klt x-fracpi4ltfracpi2+pi k)
(fracpi4+fracpi3+pi klt xltfracpi4+fracpi2+pi k)
(frac+pi klt xltfrac+pi k)
Ответ: (left(frac+pi k; frac+pi kright))

Видео:10 класс, 22 урок, Простейшие тригонометрические уравнения неравенстваСкачать

Решение задач по математике онлайн

//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘

Видео:КАК РЕШАТЬ ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ? // УРАВНЕНИЕ COSX=AСкачать

Калькулятор онлайн.
Решение тригонометрических неравенств.

Этот математический калькулятор онлайн поможет вам решить тригонометрическое неравенство. Программа для решения тригонометрического неравенства не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс получения результата.

Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Обязательно ознакомьтесь с правилами ввода функций. Это сэкономит ваше время и нервы.
Правила ввода функций >> Почему решение на английском языке? >> С 9 января 2019 года вводится новый порядок получения подробного решения некоторых задач. Ознакомтесь с новыми правилами >> —> Введите тригонометрическое неравенство
Решить неравенство

Видео:Простейшие тригонометрические уравнения. y=cosx. 1 часть. 10 класс.Скачать

Немного теории.

Видео:Решение тригонометрических неравенств. 10 класс.Скачать

Тригонометрические неравенства

Видео:Решение тригонометрических неравенств. 10 класс.Скачать

Неравенства вида ( sin x > a ) и ( sin x

Пусть дано простейшее неравенство ( sin x > a ).
1) При (-1 1 ) решением неравенства является любое действительное число: ( x in mathbb )
3) При (а = 1 ) решением неравенства является любое действительное число, отличное от ( frac + 2pi k, ; k in mathbb )
4) При (а leqslant -1 ) неравенство не имеет решений.

Видео:Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

Неравенства вида ( cos x > a ) и ( cos x

Пусть дано простейшее неравенство ( cos x > a ).
1) При (-1 1) решением неравенства является любое действительное число: ( x in mathbb )
3) При (a leqslant -1) неравенство не имеет решений.
4) При (a = 1) решением неравенства является любое действительное число, отличное от ( 2pi k, ; k in mathbb )

Видео:Отбор корней по окружностиСкачать

Неравенства вида ( tg ;x > a ) и ( tg ;x

Пусть дано простейшее неравенство ( tg ;x > a ).
Множество всех решений данного тригонометрического неравенства будем искать с помощью тригонометрического круга.

Из данного рисунка видно, что при любом (a in mathbb ) решение неравенства будет таким:
$$ x in left(arctg ;a + pi k; ;; frac + pi k right), ; k in mathbb $$

Пусть дано простейшее неравенство ( tg ;x

Видео:9 класс. Геометрия. Тригонометрические функции угла от 0° до 180°. Единичная окружность. Урок #1Скачать

Неравенства вида ( ctg ;x > a ) и ( ctg ;x

Пусть дано простейшее неравенство ( ctg ;x > a ).
Множество всех решений данного тригонометрического неравенства будем искать с помощью тригонометрического круга.

Из данного рисунка видно, что при любом (a in mathbb ) решение неравенства будет таким:
$$ x in ( pi k; ;; arcctg ;a + pi k ), ; k in mathbb $$

Пусть дано простейшее неравенство ( ctg ;x

Видео:Решение тригонометрических неравенств. Практическая часть. 10 класс.Скачать

Решение тригонометрических неравенств

ПРИМЕР 1. Решим неравенство ( sin x > frac ).
Так как ( -1 frac ).
Так как ( -1 1 ).
Очевидно, что решение неравенства будет таким:
$$ x in left(frac + pi k; ;; frac + pi kright), ; k in mathbb $$

ПРИМЕР 6. Решим неравенство ( tg ;x frac<sqrt> ).
Очевидно, что решение неравенства будет таким:
$$ x in left( pi k; ;; frac + pi k right), ; k in mathbb $$

ПРИМЕР 8. Решим неравенство ( ctg ;x

💡 Видео

Решение неравенства cos t меньше 1/2Скачать

Решение тригонометрических неравенств. 10 класс.Скачать

100 тренировочных задач #150 / Решите неравенство |sinx|≥|cosx|Скачать

Тригонометрические неравенства, часть 1Скачать

§33 Уравнение cos x = aСкачать

Алгебра 10 класс (Урок№41 - Уравнение cos x = a.)Скачать

Решение тригонометрических неравенств. 10 класс.Скачать

Уравнение cosx =aСкачать

4 способа решить уравнение sinx = cosxСкачать