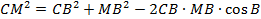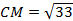Cos угла в треугольнике непрямоугольном

О чем эта статья:

Видео:СИНУС И КОСИНУС ЛЮБЫХ УГЛОВ | ТригонометрияСкачать

Формулировка и доказательство теоремы косинусов

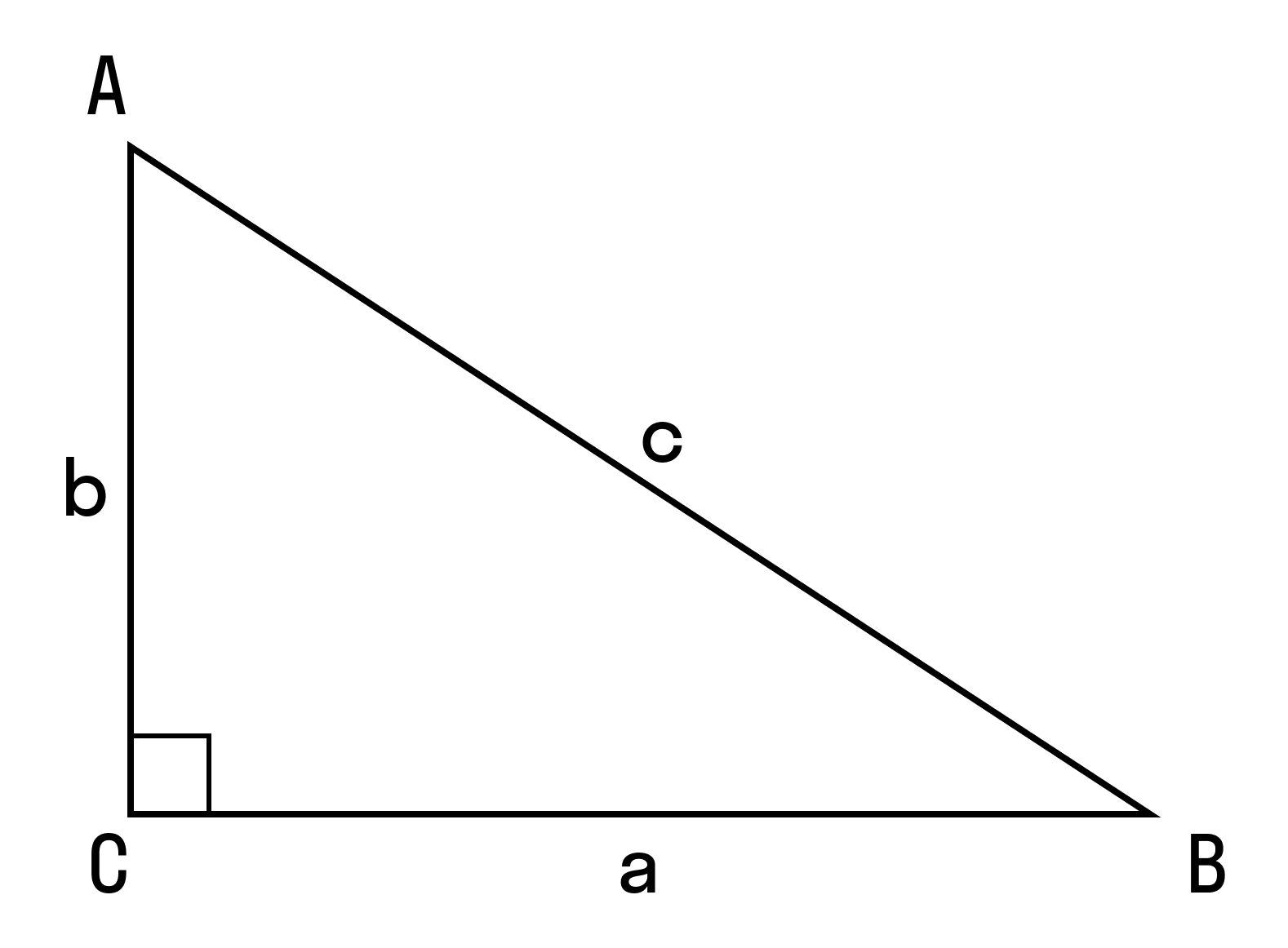
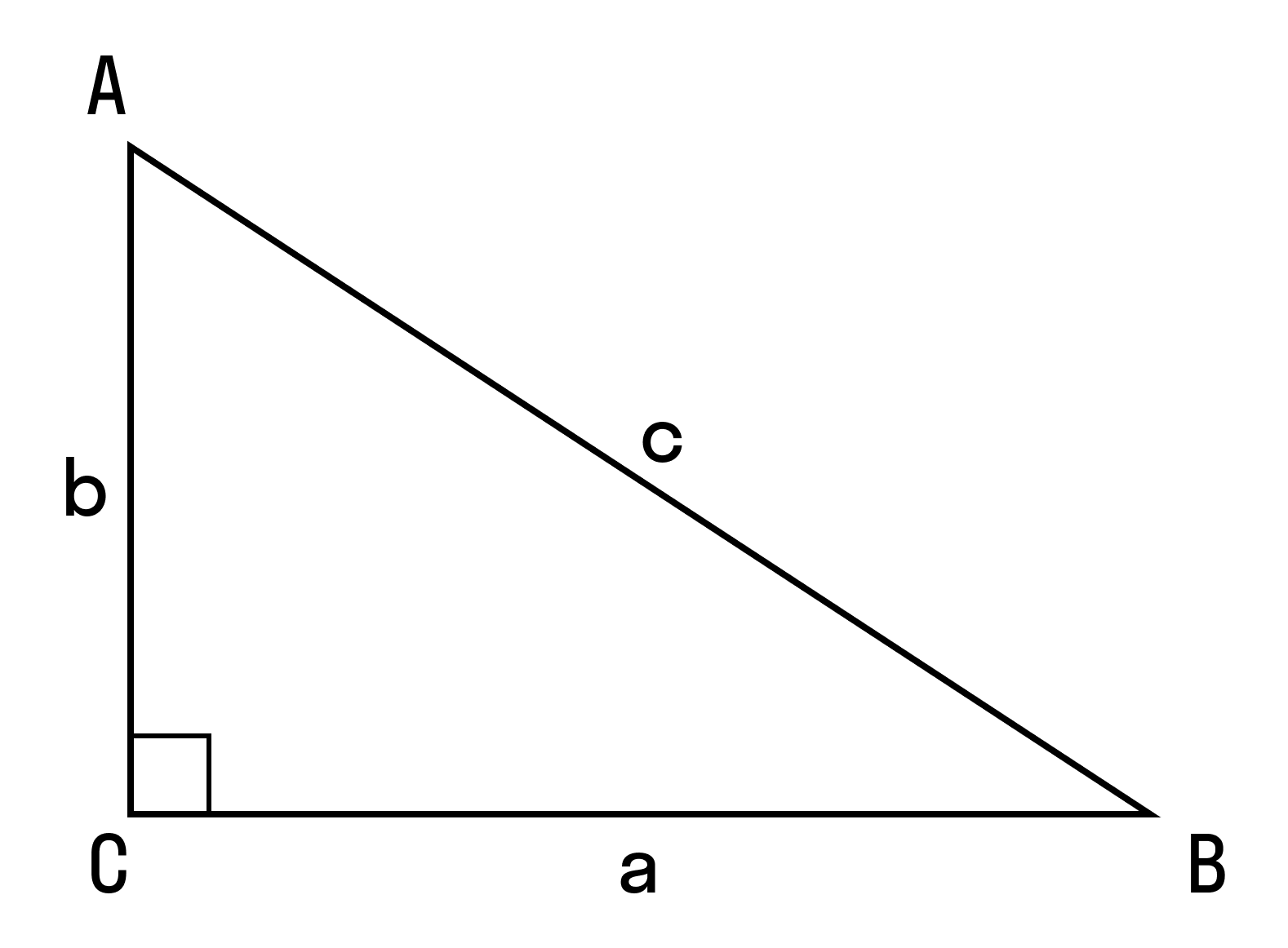
Для начала вспомним теорему Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Формула Теоремы Пифагора:

a 2 > + b 2 > = c 2 >, где a, b — катеты, с — гипотенуза.

Теорема косинусов звучит так: квадрат стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними.

Формула теоремы косинусов:

a 2 = b 2 + c 2 — 2bc cos α

В доказательстве теоремы косинусов используем формулу длины отрезка в координатах. Рассмотрим данную формулу:

В доказательстве теоремы косинусов BC — это сторона треугольника АВС, которая обозначена буквой а. Введем удобную систему координат и найдем координаты нужных нам точек. У точки В координаты (с; 0).
Координаты точки С — (b cos α; b sin α) при α ∈ (0° ; 180°).

cos 2 α + sin 2 α = 1 — основное тригонометрическое тождество.

BC 2 = a 2 = (b cos α — c) 2 + b 2 sin 2 α = b 2 cos 2 α + b 2 sin 2 α — 2bc cos α + c 2 = b 2 (cos 2 α + sin 2 α) — 2bc cos α + c 2

Что и требовалось доказать.

Совет: чтобы быстрее разобраться в сложной теме, запишитесь на онлайн-курсы по математике для детей и подростков.

С помощью теоремы косинусов можно найти косинус угла треугольника:

• Когда b 2 + c 2 — a 2 > 0, угол α будет острым.
• Когда b 2 + c 2 — a 2 = 0, угол α будет прямым.
• Когда b 2 + c 2 — a 2

Сформулируем еще одно доказательство теоремы косинусов.

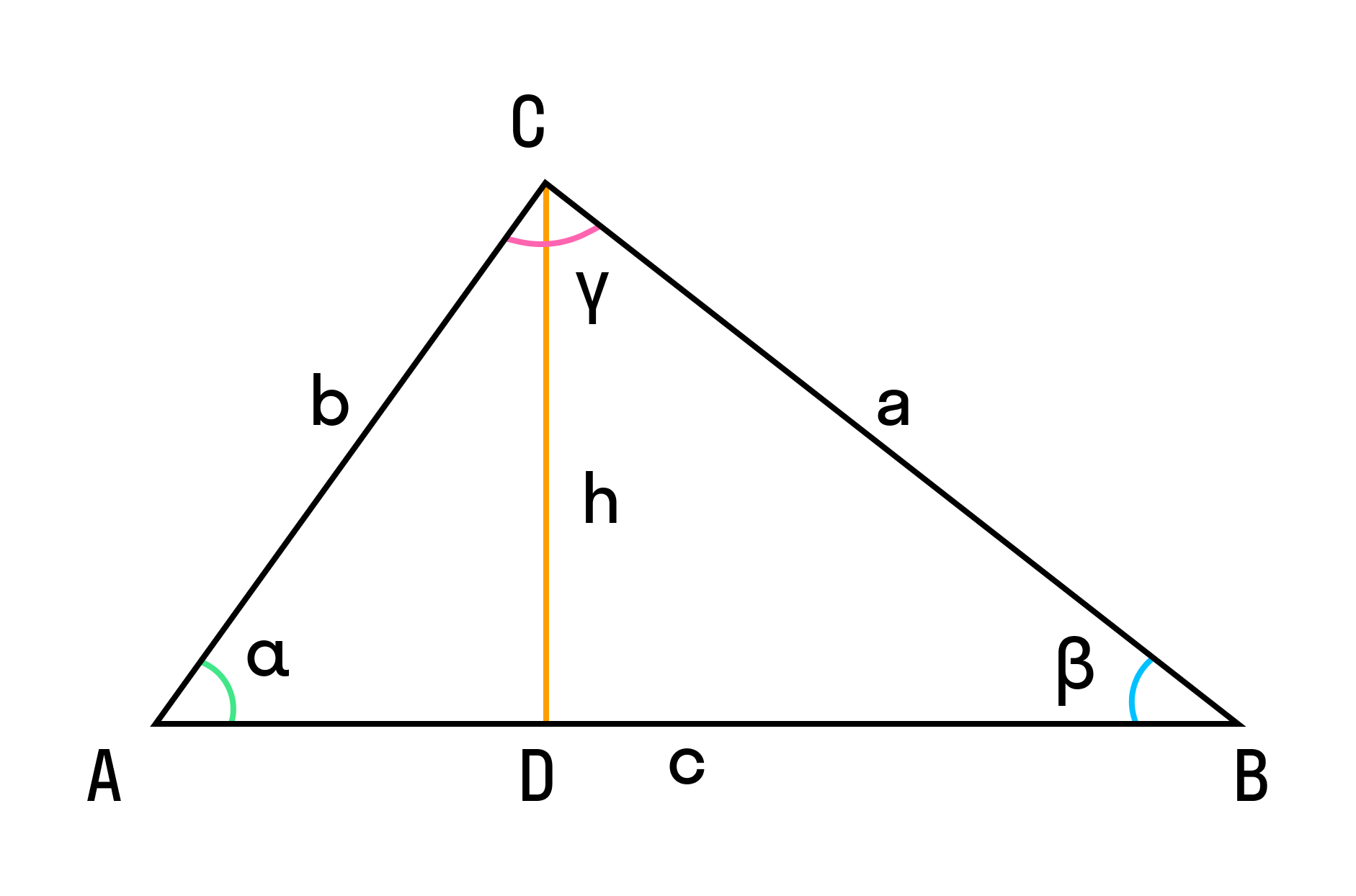
Пусть нам дан треугольник ABC, в котором из вершины C на сторону AB опустили высоту CD. Это значит:

• AD = b × cos α,
• DB = c – b × cos α.

Запишем теорему Пифагора для двух прямоугольных треугольников ADC и BDC:

• h 2 = b 2 — (b × cos α) 2
• h 2 = a 2 — (c – b × cos α) 2

Приравниваем правые части уравнений:

• b 2 — (b × cos α) 2 = a 2 — (c — b × cos α) 2

• a 2 = b 2 + c 2 — 2bc × cos α

Если один из углов при основании тупой (высота упирается в продолжение основания), полностью аналогичен рассмотренному выше.

Определим стороны b и c:

• b 2 = a 2 + c 2 — 2ac × cos β;
• c 2 = a 2 + b 2 — 2ab × cos γ.

Видео:Синус, косинус, тангенс, котангенс за 5 МИНУТСкачать

Формулировка теоремы для каждой из сторон треугольника

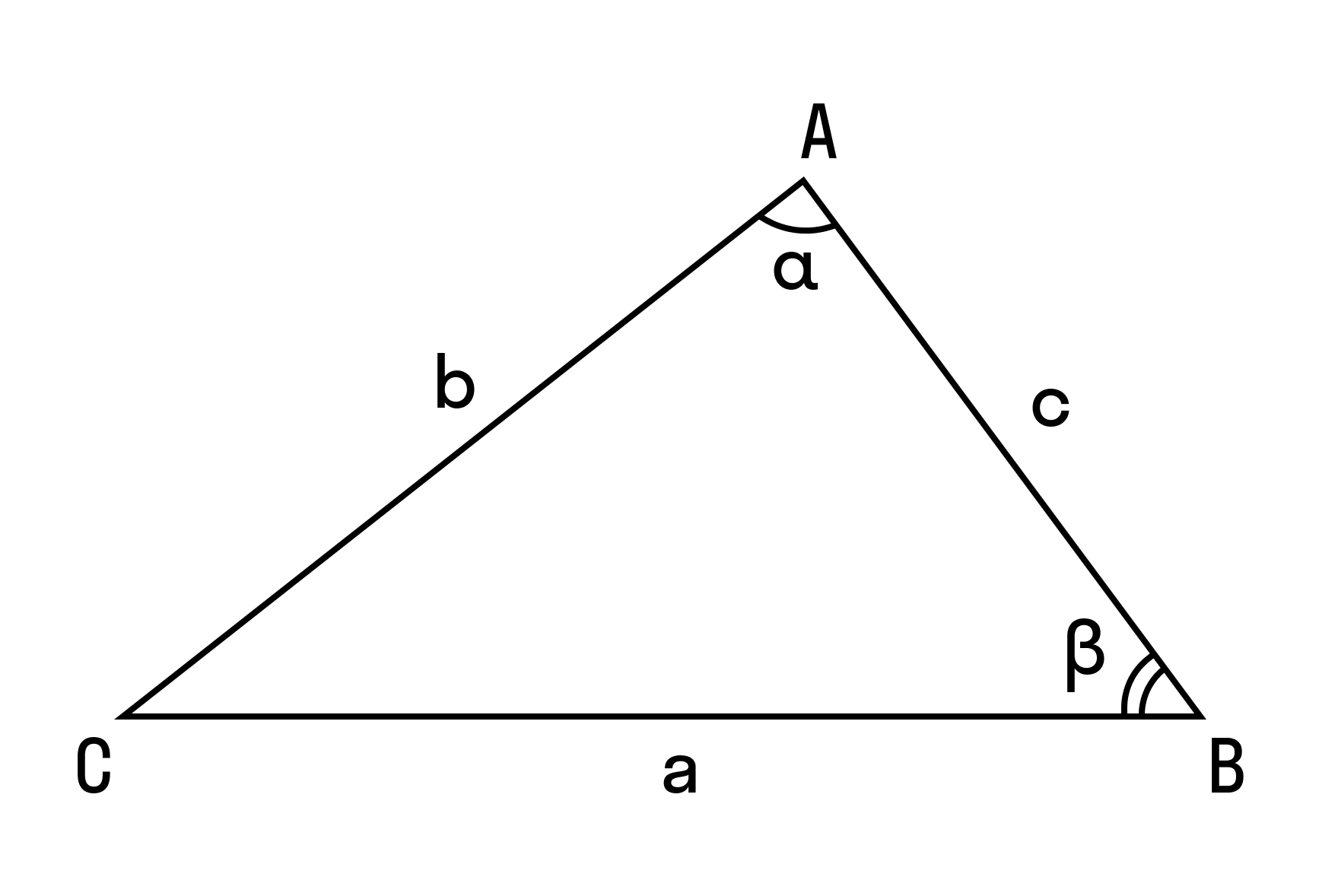
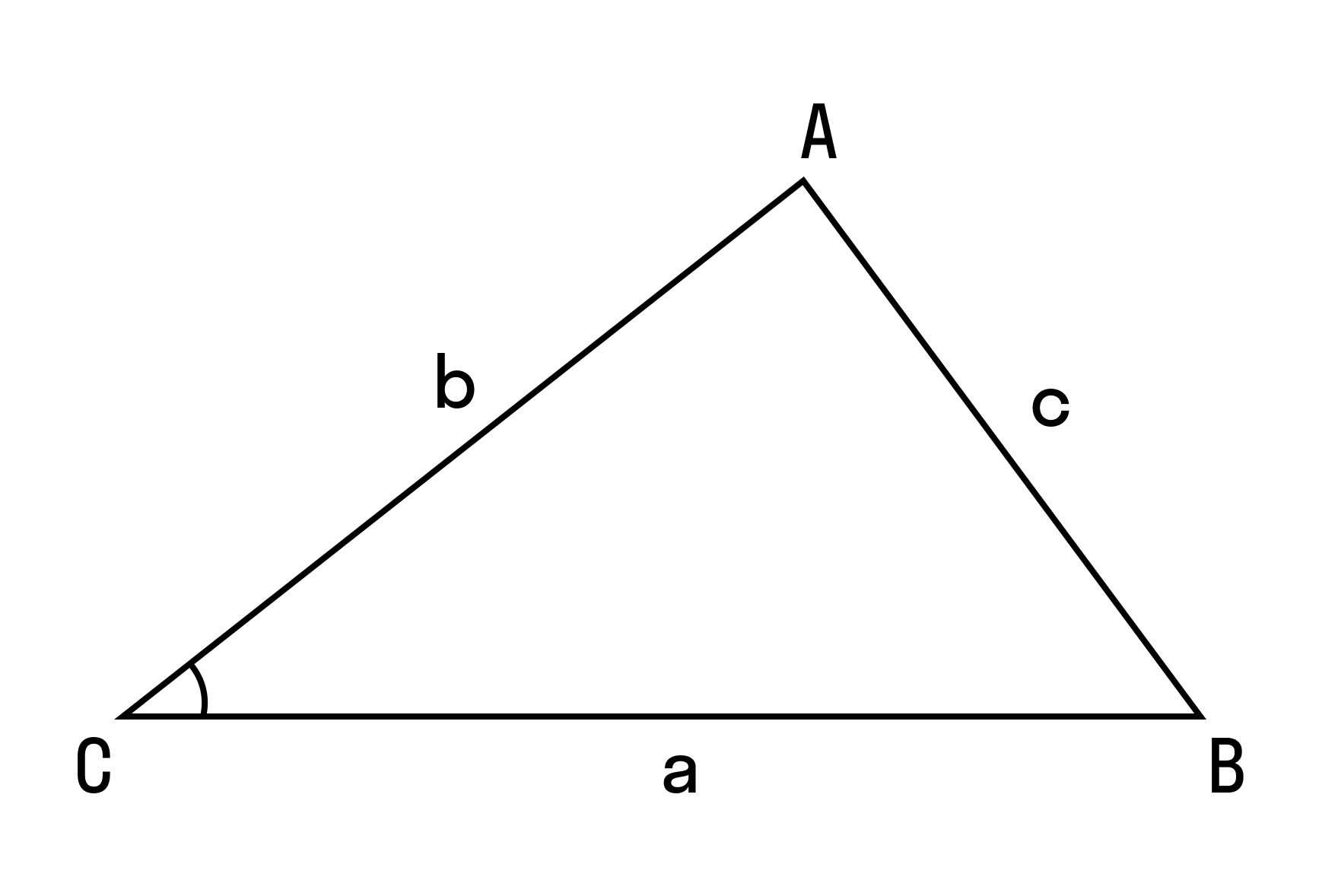
Теорема косинусов справедлива для всех сторон треугольника, то есть:

a 2 = b 2 + c 2 — 2bc cos α

b 2 = c 2 + a 2 — 2ca cos β

c 2 = a 2 + b 2 — 2ab cos γ

Теорема косинусов может быть использована для любого вида треугольника.

Видео:ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

Косинусы углов треугольника

Теорема косинусов позволяет найти как косинус, так и угол треугольника. Найдём косинусы углов:

Видео:ТРИГОНОМЕТРИЯ с нуля — Синус, косинус, тангенс и котангенс острого углаСкачать

Определение угла с помощью косинуса

А теперь обратим внимание на углы.

Как мы уже знаем, косинус угла из промежутка (0°; 180°) определяет угол (в отличие от его синуса).

Пусть нам дана единичная полуокружность. Если нам задан cos α, то нам задана точка на верхней полуокружности и задан угол α. Следовательно, cos α однозначно определяет точку М(cos α; sin α), и однозначно определяется угол ∠AOM.

Видео:Геометрия 8. Урок 11- Синус, Косинус, Тангенс и Котангенс угла в прямоугольном треугольнике.Скачать

Рассмотрение пределов изменения cos α и sin α

Рассмотрим пределы изменения синуса и косинуса α. Вспомним, что если α — угол треугольника, то он лежит в пределах от 0° до 180°.

Предел изменения косинуса: -1 0, то α ∈ (0°;90°)
Если cos α

Видео:Синус, косинус произвольного угла. 9 класс.Скачать

Примеры решения задач

При помощи теоремы косинусов можно решать задачки по геометрии. Рассмотрим интересные случаи.

Пример 1. Дан треугольник АВС. Найти длину СМ.

∠C = 90°, АВ = 9, ВС = 3, AM/MB = 1/2, где М — точка на гипотенузе АВ.

Так как АМ + МВ = 9, а AM/MB = 1/2, то АМ = 3, МВ = 6.
Из треугольника АВС найдем cos B:

Из треугольника СМВ по теореме косинусов найдём СМ:

Пример 2. Дан треугольник АВС, в котором a2+ b22 + b 2 2 , то cos C 2 = a 2 + b 2 , то ∠C = 90°.

• Если c 2 2 + b 2 , то ∠C — острый.

Видео:ТРИГОНОМЕТРИЯ | Синус, Косинус, Тангенс, КотангенсСкачать

Теорема косинусов. Доказательство теоремы косинусов.

Теорема косинусов — теорема евклидовой геометрии, которая обобщающает теорему Пифагора.

Теорема косинусов:

Для плоского треугольника, у которого стороны a, b, c и угол α, который противолежит стороне a, справедливо соотношение:

Квадрат стороны треугольника равняется сумме квадратов 2-х других сторон минус удвоенное произведение этих сторон на косинус угла между ними.

Видео:8 класс, 29 урок, Синус, косинус и тангенс острого угла прямоугольного треугольникаСкачать

Следствие из теоремы косинусов.

• Теорема косинусов используется для определения cos угла треугольника:

h 2 = a 2 — (c – b cos α) 2 (2)

Приравниваем правые части уравнений (1) и (2):

b 2 — (b cos α) 2 = a 2 — (c — b cos α) 2

a 2 = b 2 + c 2 — 2bc cos α.

Если 1-н из углов при основании тупой (высота упирается в продолжение основания), полностью аналогичен рассмотренному выше.

Определить стороны b и c:

Видео:Геометрия 8 класс (Урок№21 - Косинус, синус и тангенс острого угла прямоугольного треугольника.)Скачать

Теорема косинусов

Теорема косинусов — в любом треугольнике квадрат одной стороны равен сумме квадратов двух других сторон минус удвоенное произведение этих двух сторон на косинус угла между ними.

• a² = b² + c² – 2b.c.cosα
• b² = a² + c² – 2a.c.cosβ
• c² = a² + b² – 2a.b.cosγ

Например:

Одна сторона треугольника равна 12 см, другая — 8 см, между ними образовался угол 120º. Найдите длину третьей стороны.

Решение по формуле a² = b² + c² – 2b.c.cosα:

cos α = cos 120º = — 1/2 (это значение можно найти в таблицах)

a² = 12² + 8² – 2×12×8×(- 1/2)

Длина третьей стороны — примерно 17,436 см.

Видео:ОГЭ как найти тангенс угла, если нет треугольника #математика #огэ #огэматематика #геометрияСкачать

Следствия

Следствие косинуса угла треугольника

При помощи теоремы косинусов можно найти косинус угла треугольника.

Используйте теорему косинусов, чтобы найти угол β.

Решение:

Будем использовать эту версию формулы:

cos β = (6² + 8² − 7²) / 2×6×8

Следствие верхней части формулы cos α

Чтобы узнать, если угол α острый, прямой или тупой, нужно вычислить b²+c²−a² (это верхняя часть формулы для cos α):

• b²+c²−a² 0, значит угол α — острый.

Видео:Как просто запомнить, что такое sin, cos, tg?! #косинус #синус #тангенс #математика #огэ #егэСкачать

Доказательство теоремы косинусов

Нужно доказать, что c² = a² + b² − 2a.b.cos C

1. Из определения косинуса известно, что в прямоугольном треугольнике BCD: cos C = CD/a CD = a.cos C.

2. Вычитаем это из стороны b, так мы получим DA:

3. Мы знаем из определения синуса, что в том же треугольнике BCD:

sin C = BD/a BD = a.sinC.

4. Применяем теорему Пифагора в треугольнике ADB: c² = BD² + DA²

5. Заменим BD и DA из пунктов 2) и 3), получится выражение: c²= (a. sin C)²+(b−a.cos C)²

6. Раскрываем скобки: c² = a² sin ²C + b² − 2a.b.cosC + a².cos²C

6.1. Поменяем их местами (a²cos²C поставим на второе место): c² = a² sin ²C + a²cos²C + b² − 2a.b.cosC

7. Выносим за скобки «a²»: c² = a² (sin²C+cos²C) + b² − 2a.b.cosC

8. В скобках получилось основное тригонометрическим тождество (sin²α + cos²α = 1), значит его можно сократить т. к. умножение на единицу ничего не меняет, получилось: c² = a² + b² − 2a.b.cos C

Видео:Синус, косинус, тангенс ТУПОГО угла | Твой самый халявний балл на ОГЭ 2023!Скачать

Теорема косинусов для равнобедренного треугольника

В равнобедренном треугольнике:

• две его стороны равны;
• углы при основании равны.

Используем формулу теоремы косинусов

a² = b² + c² – 2b.c.cosα

Подставляем все известные:

x² = 8² + 8² – 2×8×8×cos140º

x² = 64 + 64 – 128 × (-0,766)

Видео:ОГЭ по математике. В треугольнике АБС известно три стороны. Найди косинус угла. (Вар.8) √ 16Скачать

Теорема синусов

Теорема синусов гласит, что отношение стороны треугольника к синусу угла, противолежащего данной стороне, одинаково для всех сторон и углов в данном треугольнике:

📹 Видео

Математика | Соотношения между сторонами и углами в прямоугольном треугольнике.Скачать

Геометрия 9 класс (Урок№12 - Синус, косинус, тангенс, котангенс угла.)Скачать

Нахождение стороны прямоугольного треугольникаСкачать

Что такое синус, косинус и тангенс угла в прямоугольном треугольнике. Часть 1Скачать

Урок СИНУС, КОСИНУС И ТАНГЕНС ОСТРОГО УГЛА ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКАСкачать

68. Синус, косинус и тангенс острого угла прямоугольного треугольникаСкачать

Тригонометрия: Как запомнить? + ПОЛУЧИ ПОДАРОК от Ольги АлександровныСкачать