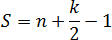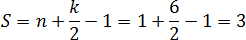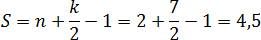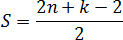Что такое узел окружности

Понятие узла интуитивно представляется ясным. Простейшими примерами узлов являются простой узел (рис. 41) и восьмерка (рис. 42).

Их нетрудно изобразить с помощью нити. Эти узлы различны, так как любые попытки перевести простой узел, называемый также трилистником, в восьмерку, не протаскивая при этом концы через петлю, оканчиваются неудачей.

Если склеить концы трилистника и восьмерки (рис. 43, 44), то каждый из этих узлов представляет тогда несамопересекаю- щуюся замкнутую кривую в пространстве. Это значит, что каждая такая кривая топологически эквивалентна окружности, но, тем не менее, деформировать узел в окружность без разрыва невозможно.

Узлы естественно различать по числу «пересечений», то есть таких точек, в которых кривая проходит «над собой». Очевидно, для трилистника это число равно трем, а для восьмерки — четырем.

Можно рассматривать зацепления двух или более замкнутых кривых. В этом случае говорят просто о зацеплениях. Характер зацепления зависит от того, сколько раз меняет одна кривая свое расположение относительно другой с «над» на «под». Это число называют коэффициентом зацепления. На рисунке 45 (а, б, в, г) показаны примеры зацеплений, коэффициенты которых равны соответственно 0, 1, 4, 4.

Коэффициент зацепления может оказаться равным нулю, но кривые зацеплены. На рисунке 46 показано такое зацепление трех колец. Видно, что никакие два из трех данных колец не зацеплены, тем не менее расцепить эти кольца, не разрезая ни одного из них, невозможно. Такое зацепление называют кольцами Борромео (название древнего итальянского рода, чьи воины носили на одежде нашивки из трех таким образом переплетенных колец).

Три венка: лавровый, оливковый и дубовый, сцепленные как кольца Борромео, украшают надгробье Микеланджело. Они символизируют скульптуру, живопись и архитектуру — три вида искусств, в которых прославился Микеланджело Буона- ротти. Такое же переплетение венков изображено и на медали, отчеканенной в честь великого художника.

Зацепление колец Борромео характеризуется тем, что разрез любого кольца приводит к распаду всего зацепления. Можно переплести любое число колец, обладающих тем же свойством, если кольца расположить в виде цепочки. Подобные цепочки обладают важным практическим преимуществом — их можно собирать из целых звеньев (рис. 47).

Таким образом, узлы — это несамопересекающиеся замкнутые кривые в трехмерном евклидовом пространстве. Первым, кто рассматривал узлы как математические объекты, был К. Гаусс (1777—1855). Он считал, что изучение явлений заузливания является одной из основных задач так называемой геометрии положения. Сам К. Гаусс мало написал об узлах, однако его ученик И. Листинг посвятил узлам значительную часть своей монографии «Предварительные исследования по топологии» (1847). Зацепления — это некоторое расположение двух или более замкнутых кривых в трехмерном евклидовом пространстве.

• 1. Что такое узел? В чем отличие трилистника от восьмерки? Как это отличие может быть выражено количественно?
• 2. Что такое коэффициент зацепления? Нарисуйте зацепление двух кривых, коэффициент которого равен 8.
• 3. В чем особенность зацепления колец Борромео? Чему равен коэффициент этого зацепления?

1. Найдите коэффициенты зацепления каждой пары колец Олимпийской эмблемы (рис. 48).

2. Нарисуйте зацепление пяти колец так, чтобы каждые три из них были зацеплены как кольца Борромео.

3. Распадется ли зацепление, изображенное на рисунке 49, если разрезать среднее кольцо? [1]

Видео:Математика это не ИсламСкачать

Метод узлов в задаче B5

Существует замечательная формула, которая позволяет считать площадь многоугольника на координатной сетке почти без ошибок. Это даже не формула, а настоящая теорема. На первый взгляд, она может показаться сложной. Но достаточно решить пару задач — и вы поймете, насколько это крутая фишка. Так что вперед!

Для начала введем новое определение:

— это любая точка, лежащая на пересечении вертикальных и горизонтальных линий этой сетки.

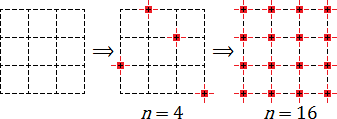
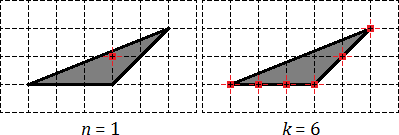
На первой картинке узлы вообще не обозначены. На второй обозначены 4 узла. Наконец, на третьей картинке обозначены все 16 узлов.

Какое отношение это имеет к задаче B5? Дело в том, что вершины многоугольника в таких задачах всегда лежат в узлах сетки. Как следствие, для них работает следующая теорема:

Теорема. Рассмотрим многоугольник на координатной сетке, вершины которого лежат в узлах этой сетки. Тогда площадь многоугольника равна:

где n — число узлов внутри данного многоугольника, число узлов, которые лежат на его границе (граничных узлов).

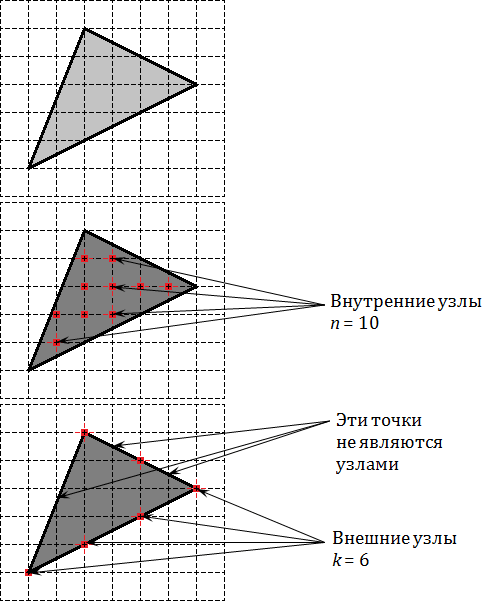
В качестве примера рассмотрим обычный треугольник на координатной сетке и попробуем отметить внутренние и граничные узлы.

На первой картинке дан обычный треугольник. На второй отмечены его внутренние узлы, число которых равно На третей картинке отмечены узлы лежащие на границе, их всего

Возможно, многим читателям непонятно, как считать числа Начните с внутренних узлов. Тут все очевидно: закрашиваем треугольник карандашом и смотрим, сколько узлов попало под закраску.

С граничными узлами чуть сложнее. Граница многоугольника — замкнутая ломаная, которая пересекает координатную сетку во многих точках. Проще всего отметить какую-нибудь «стартовую» точку, а затем обойти остальные.

Граничными узлами будут только те точки на ломаной, в которых одновременно пересекаются

1. Собственно, ломаная;
2. Горизонтальная линия координатной сетки;
3. Вертикальная линия.

Посмотрим, как все это работает в настоящих задачах.

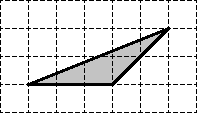
Задача. Найдите площадь треугольника, если размер клетки равен 1 x 1 см:

Для начала отметим узлы, которые лежат внутри треугольника, а также на его границе:

Получается, что внутренний узел всего один: Граничных узлов — целых шесть: три совпадают с вершинами треугольника, а еще три лежат на сторонах.

Теперь считаем площадь по формуле:

Вот и все! Задача решена.

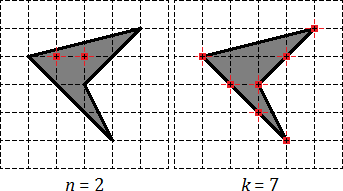
Задача. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см на 1 см. Ответ дайте в квадратных сантиметрах.

Снова отмечаем внутренние и граничные узлы. Внутренних узлов всего Граничных узлов: из которых 4 являются вершинами четырехугольника, а еще 3 лежат на сторонах.

Остается подставить числа в формулу площади:

Обратите внимание на последний пример. Эту задачу реально предлагали на диагностической работе в 2012 году. Если работать по стандартной схеме, придется делать много дополнительных построений. А методом узлов все решается практически устно.

Видео:Александра Скрипченко - Теория узловСкачать

Важное замечание по площадям

Но формула — это еще не все. Давайте немного перепишем формулу, приведя слагаемые в правой части к общему знаменателю. Получим:

Числа n и k — это количество узлов, они всегда целые. Значит, весь числитель тоже целый. Мы делим его на 2, из чего следует важный факт:

Площадь всегда выражается целым числом или дробью. Причем в конце дроби всегда стоит «пять десятых»: 10,5; 17,5 и т.д.

Таким образом, площадь в задаче B5 всегда выражается целым числом или дробью Если ответ получается другим, значит, где-то допущена ошибка. Помните об этом, когда будете сдавать настоящий ЕГЭ по математике!

Видео:Исследования в теории узлов MITСкачать

Статья по математике на тему: «Понятия узлов»(11 класс)

Видео:Knots 1Скачать

«Календарь счастливой жизни:
инструменты и механизм работы
для достижения своих целей»

Сертификат и скидка на обучение каждому участнику

ГАОУ СПО НСО «НКАиДХ»

Научный руководитель Кухарева И.М.

Понятие математического узла

Узлыпредметы простые и наглядные. Вы, конечно, встречались с ними в повседневной жизни, но, может быть, не подозревали, что это ещё и математические объекты; более того, в последние 20 лет математики и физики с огромным интересом и удивительной интенсивностью стали заниматься соответствующими теориями, особенно теорией узлов. Достаточно сказать, что за это время четыре медали Филдса были получены именно за работы, связанные с этой теорией. А именно, лауреатами медали Филдса в разное время стали Владимир Дринфельд из Харькова, работающий в Чикаго, Максим Концевич из Москвы, работающий в Париже, Воган Джонс из Новой Зеландии, работающий в Калифорнии, и Эдвард Виттен , физик-теоретик, работающий в Принстоне.

Чем отличается математический узел от узлов , которые завязывают на галстуках или на шнурках

ботинок? Естественно, в математике узел — это некая абстракция: рассматривается не верёвка и не шнур, а бесконечно тонкая, гибкая и растяжимая нить. Кроме того, рассматривая математический узел, нужно либо как -то зафиксировать его концы (обычно говорят, что один конец уходит в бесконечность «вверх», а другой —в бесконечность «вниз», либо просто соединить их (см. рис.). В последнем случае модель узла — замкнутаянесамопересекающаяся кривая в пространстве. Будем предполагать, что эта кривая является ломаной, тоесть состоит из отрезков (впрочем, на рисунках мы почти всегда будем изображать узлы в виде гладких кривых, считая отдельные звенья ломаной. Самый простой узел — тривиальный (простая окружность ). Узел называется нетривиальным, если он не эквивалентен тривиальному, то есть его нельзя «пошевелить» (возможно растягивая, но не разрывая верёвку) так, чтобы он превратился в тривиальный.

Трилистник и восьмёрка

Вот несколько примеров нетривиальных узлов: узел на рис. слева называется трилистником , узел на рис. справа — восьмёркой . (Обычно узлы рассматривают с ориентацией, то есть считают, что задано направлениеобхода кривой, это направление изображается стрелкой.)

А можно ли умножать узлы? Если считать узлы кривыми, концы которых уходят в бесконечность, тоумножение узлов определяется естественным образом: произведение узлов а и b — это просто нить, накоторой завязан сначала узел а, затем узел b (рис. справа). Это умножение ассоциативно: для любых узлов а,b и с верно равенство: (ab)c=a(bc). Ясно, что тривиальный узел (то есть просто вертикальная прямая)является единичным элементом. Ни один нетривиальный узел не имеет обратного. Покажем, что два узла,завязанные на одной веревке, можно переставить. Действительно, пусть на нити завязан сначала узел a,затем узел b. Сперва, не трогая узел a, «затянем» узел b в маленький узелок. Потом заключим этот узелок вмаленький стеклянный шарик и будем двигать его вверх по нити. В итоге этот шарик окажется наверху, и егоможно превратить опять в узел b. Таким образом, умножние узлов коммутативно: ab=ba.
Итак, верна
Теорема об узлах. Узлы образуют ассоциативную и коммутативную систему относительно умножения. В этойсистеме есть единичный элемент, но нет обратных.

Компьютер развязывает узлы

Первый шаг в этой теории состоит в сведении (сложной) пространственной задачи развязывания узла к(более простой) задаче применения простых операций к кривым на плоскости. Эти операции придумал в 1920-е годы немецкий математик Рейдемейстер .

Журнал GEO непознанный мир: земля №01(166) январь 2012

📹 Видео

Лекция 1 | Теория узлов | Обзор одного снаСкачать

Теория узлов: от шнурков до новых молекул [Veritasium]Скачать

Интуитивная теория узлов | примеры нетривиальных узлов, задачи теории узлов, операция связной суммы.Скачать

✓ Всё, что нужно знать про окружность | ЕГЭ. Задания 1 и 16. Профильный уровень | Борис ТрушинСкачать

Скорость в морских узлах - история единицы измеренияСкачать

Интуитивная теория узлов | понятие диаграммы узла и преобразования РайдемайстераСкачать

Интуитивная теория узлов | фундаментальная группа узлов и зацеплений | определениеСкачать

Интуитивная теория узлов | примеры узлов | торические узлыСкачать

Интуитивная теория узлов | начала теории кос | 1Скачать

Введение в теорию узлов, А.Б.Сосинский, лекция 1Скачать

Интуитивная теория узлов | полином Александера | полином Александера для торических узловСкачать

Интуитивная теория узлов | поверхности Зейферта | 27 | понятие коэффициента зацепленияСкачать

Обязательно запомни эту хитрость! Как завязать надежный узел, который легко распутать? #shortsСкачать

ПОЧЕМУ СКОРОСТЬ КОРАБЛЕЙ ИЗМЕРЯЕТСЯ В УЗЛАХ ? "БУДЬ В КУРСЕ"Скачать

Как вязать узлы. 10 самых нужных узлов.Скачать

Лекция 5 | Инварианты узлов | Максим Карев | ЛекториумСкачать