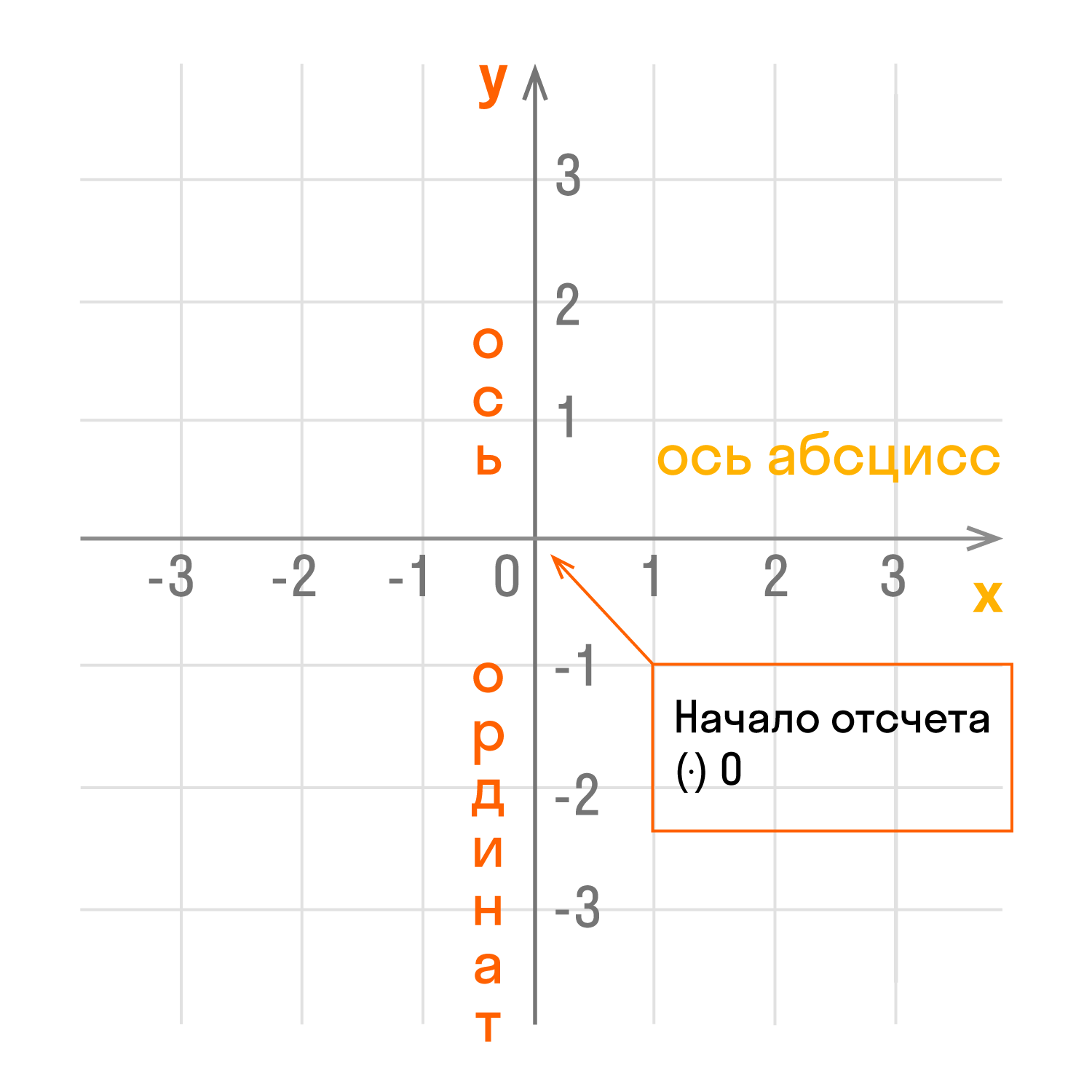
Термин «абсцисса» широко используется в геометрии. Абсциссой называют координату точки на оси X’X в прямоугольной системе координат. В переводе с латинского языка «abscissa» означает «отрезок». Итак, разберём подробнее, что же представляет собой абсцисса.
У плоской системы координат имеются оси X’X и Y’Y. Именно ось X’X и есть ось абсцисс, а так называемая ось Y’Y – это ось ординат. Предположим, что мы имеем некую точку A в плоской системе координат. У данной точки есть свои координаты X и Y. Расстояние от точки A до оси ординат Y’Y и называют абсциссой точки. Это может быть положительное или отрицательное значение, а также значение равное нулю.
Если точка A будет принадлежать положительной полуоси OX, то значение абсциссы будет положительным, если отрицательной полуоси X’O, то соответственно значение абсциссы будет отрицательным. Последним возможным вариантом является случай, когда точка A лежит на оси Y’Y, тогда её абсцисса равна нулю.
В прямоугольной системе координат прямую X’X (или так называемый «луч») именуют «осью абсцисс». Строя графики функций, ось абсцисс обычно используют в качестве области определения функции.
Вместе со статьёй «Что такое абсцисса?» читают:
Видео:10 класс, 11 урок, Числовая окружностьСкачать

Значение слова «абсцисса»
АБСЦИ́ССА, -ы, ж. Мат. Одна из трех координат, определяющих положение точки в пространстве.
[От лат. abscissa — отсеченная, отрезанная]
Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека
- Абсциссой точки A называется координата этой точки на оси X’Х в прямоугольной системе координат. Величина абсциссы точки A равна длине отрезка OB (см. рисунок). Если точка B принадлежит положительной полуоси OX, то абсцисса имеет положительное значение. Если точка B принадлежит отрицательной полуоси X’O, то абсцисса имеет отрицательное значение. Если точка A лежит на оси Y’Y, то её абсцисса равна нулю.
В прямоугольной системе координат луч (прямая) X’X называется «осью абсцисс». При построении графиков функций, ось абсцисс обычно используется как область определения функции.
АБСЦИ’ССА, ы, ж. [латин. abscissa, букв. отрезанная] (мат.). Горизонтальный отрезок линии от точки пересечения координатных осей до ординаты искомой точки. На диаграмме роста сети железных дорог года нанесены на оси абсцисс.
Источник: «Толковый словарь русского языка» под редакцией Д. Н. Ушакова (1935-1940); (электронная версия): Фундаментальная электронная библиотека
абсци́сса
1. матем. координата точки на оси X в прямоугольной системе координат ◆ Перемещение точки по абсциссе вызывает сдвиг проекции по ординате.
Делаем Карту слов лучше вместе

Спасибо! Я стал чуточку лучше понимать мир эмоций.
Вопрос: увешать — это что-то нейтральное, положительное или отрицательное?
Видео:АбсциссаСкачать

Прямоугольная система координат. Ось абсцисс и ординат
О чем эта статья:
Видео:Система координат · Ось абсцисс и ось ординат · Координатная плоскость Урок Математики для 6 классаСкачать

Прямоугольная декартова система координат
Французский математик Рене Декарт предложил вместо геометрических построений использовать математические расчеты. Так появился метод координат, о котором мы сейчас расскажем.
Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Например, координаты школы тоже можно записать числами — они помогут понять, где именно находится наша школа. С точками на плоскости та же история.
Координатой можно назвать номер столика в кафе, широту и долготу на географической карте, положение точки на числовой оси и даже номер телефона друга. Проще говоря, когда мы обозначаем какой-то объект набором букв, чисел или других символов, тем самым мы задаем его координаты.
Прямоугольная система координат — это система координат, которую изобрел математик Рене Декарт, ее еще называют «декартова система координат». Она представляет собой два взаимно перпендикулярных луча с началом отсчета в точке их пересечения.
Чтобы найти координаты, нужны ориентиры, от которых будет идти отсчет. На плоскости в этой роли выступят две числовые оси.
Чертеж начинается с горизонтальной оси, которая называется осью абсцисс и обозначается латинской буквой x (икс). Записывают ось так: Ox. Положительное направление оси абсцисс обозначается стрелкой слева направо.
Затем проводят вертикальную ось, которая называется осью ординат и обозначается y (игрек). Записывают ось Oy. Положительное направление оси ординат показываем стрелкой снизу вверх.
Оси взаимно перпендикулярны, а значит угол между ними равен 90°. Точка пересечения является началом отсчета для каждой из осей и обозначается так: O. Начало координат делит оси на две части: положительную и отрицательную.
- Координатные оси — это прямые, образующие систему координат.
- Ось абсцисс Ox — горизонтальная ось.
- Ось ординат Oy — вертикальная ось.
- Координатная плоскость — плоскость, в которой находится система координат. Обозначается так: x0y.
- Единичный отрезок — величина, которая принимается за единицу при геометрических построениях. В декартовой системе координат единичный отрезок отмечается на каждой из осей. Длина отрезка показывает сколько раз единичный отрезок и его части укладываются в данном отрезке.
Единичные отрезки располагаются справа и слева от оси Oy, вверх и вниз от оси Oy. Числовые значения на оси Oy располагаются слева или справа, на оси Ox — внизу под ней. Чаще всего единичные отрезки двух осей соответствуют друг другу, но бывают задачи, где они не равны.
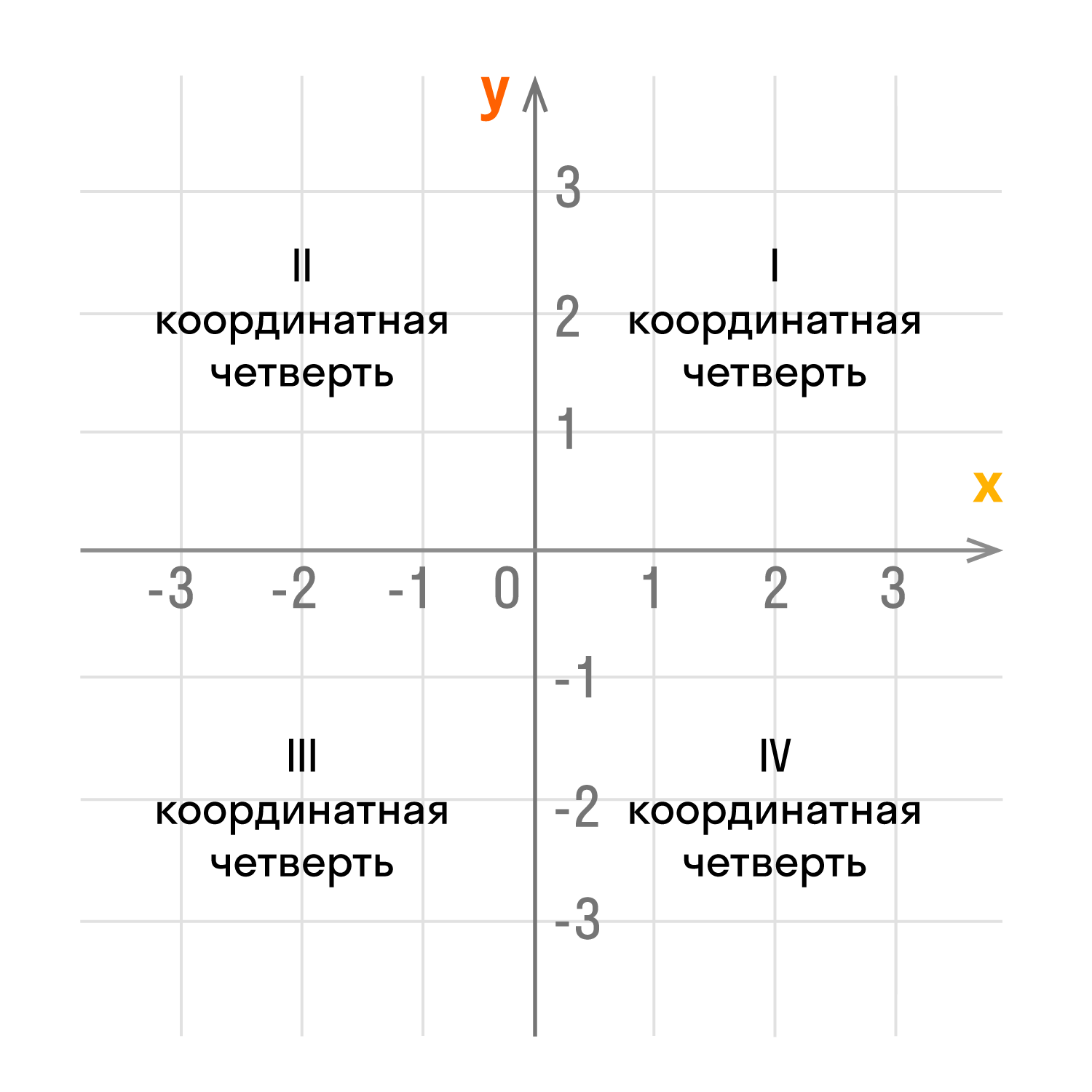
Оси координат делят плоскость на четыре угла — четыре координатные четверти.
У каждой из координатных четвертей есть свой номер и обозначение в виде римской цифры. Отсчет идет против часовой стрелки:
- верхний правый угол — первая четверть I;
- верхний левый угол — вторая четверть II;
- нижний левый угол — третья четверть III;
- нижний правый угол — четвертая четверть IV;
Чтобы узнать координаты точки в прямоугольной системе координат, нужно опустить от точки перпендикуляр на каждую ось и посчитать количество единичных отрезков от нулевой отметки до опущенного перпендикуляра. Координаты записывают в скобках, первая по оси Ох, вторая по оси Оу.
- Если обе координаты положительны, то точка находится в первой четверти координатной плоскости.
- Если координата х отрицательная, а координата у положительная, то точка находится во второй четверти.
- Если обе координаты отрицательны, то число находится в третьей четверти.
- Если координата х положительная, а координата у отрицательная, то точка лежит в четвертой четверти.
Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.
Видео:Алгебра 7 класс. 28 сентября. Зная абсциссу найти ординатуСкачать

Координаты точки в декартовой системе координат
Для начала отложим точку М на координатной оси Ох. Любое действительное число xM равно единственной точке М, которая располагается на данной прямой. При этом начало отсчета координатных прямых всегда ноль.
Каждая точка М, которая расположена на Ох, равна действительному числу xM. Этим действительным числом и является ноль, если точка М расположена в начале координат, то есть на пересечении Оx и Оу. Если точка удалена в положительном направлении, то число длины отрезка положительно и наоборот.
Число xM — это координата точки М на заданной координатной прямой.
Пусть точка будет проекцией точки Mx на Ох, а My на Оу. Значит, через точку М можно провести перпендикулярные осям Оx и Оу прямые, после чего получим соответственные точки пересечения Mx и My.Тогда у точки Mx на оси Оx есть соответствующее число xM, а My на Оу — yM. Как это выглядит на координатных осях:
Каждой точке М на заданной плоскости в прямоугольной декартовой системе координат соответствует пара чисел (xM, yM), которые называются ее координатами. Абсцисса М — это xM, ордината М — это yM.
Обратное утверждение тоже верно: каждая пара (xM, yM) имеет соответствующую точку на плоскости.
📽️ Видео
Уравнение окружности с центром на оси абсцисс, ординат или в начале координат. Урок 3. Геометрия 8.Скачать

9 класс, 6 урок, Уравнение окружностиСкачать

Координатная плоскость | Ось абсцисс | Ось ординат | МегаШкола | Математика 6 классСкачать

№1011. Ответьте на вопросы: а) Может ли абсцисса точки единичной полуокружности иметь значения 0,3Скачать
Уравнение окружности (1)Скачать

Прямоугольная система координат. Координатная плоскость. 6 класс.Скачать

ГЕОМЕТРИЯ 9 класс: Уравнение окружности и прямойСкачать

№964. На окружности, заданной уравнением (x-3)2 + + (y-5)2 = 25, найдите точки: а) с абсциссой 3;Скачать
10 класс, 12 урок, Числовая окружность на координатной плоскостиСкачать

Точки пересечения графика линейной функции с координатными осями. 7 класс.Скачать

Математика без Ху!ни. Уравнение касательной.Скачать

Абсцисса / Ордината🥲 #математика #егэ #умскулСкачать

абсциссаСкачать

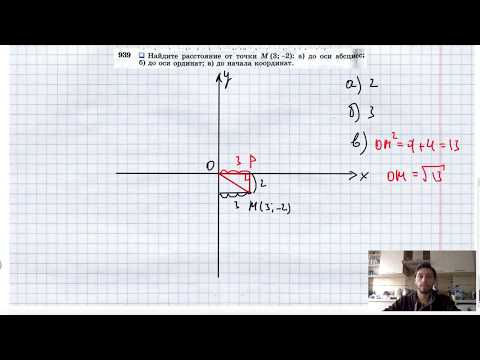
№939. Найдите расстояние от точки М (3; -2): а) до оси абсцисс; б) до оси ординат;Скачать
Как найти абсциссу точки пересечения двух прямых?Скачать

Уравнение окружностиСкачать