Число 3п 2 соответствует точке тригонометрической окружности с ординатой

Надеюсь, вы уже прочитали про числовую окружность и знаете, почему она называется числовой, где на ней начало координат и в какой стороне положительное направление. Если нет, то бегом читать ! Если вы, конечно, собираетесь находить точки на числовой окружности.

Видео:10 класс, 11 урок, Числовая окружностьСкачать

Обозначаем числа (2π), (π), (frac), (-frac), (frac)

Как вы знаете из прошлой статьи, радиус числовой окружности равен (1). Значит, длина окружности равняется (2π) (вычислили по формуле (l=2πR)). С учетом этого отметим (2π) на числовой окружности. Чтобы отметить это число нужно пройти от (0) по числовой окружности расстояние равно (2π) в положительном направлении, а так как длина окружности (2π), то получается, что мы сделаем полный оборот. То есть, числу (2π) и (0) соответствует одна и та же точка. Не переживайте, несколько значений для одной точки — это нормально для числовой окружности.

Теперь обозначим на числовой окружности число (π). (π) – это половина от (2π). Таким образом, чтобы отметить это число и соответствующую ему точку, нужно пройти от (0) в положительном направлении половину окружности.

Отметим точку (frac) . (frac) – это половина от (π), следовательно чтобы отметить это число, нужно от (0) пройти в положительном направлении расстояние равное половине (π), то есть четверть окружности.

Обозначим на окружности точки (-) (frac) . Двигаемся на такое же расстояние, как в прошлый раз, но в отрицательном направлении.

Нанесем (-π). Для этого пройдем расстояние равное половине окружности в отрицательном направлении.

Теперь рассмотрим пример посложнее. Отметим на окружности число (frac) . Для этого дробь (frac) переведем в смешанный вид (frac) (=1) (frac) , т.е. (frac) (=π+) (frac) . Значит, нужно от (0) в положительную сторону пройти расстояние в пол окружности и еще в четверть.

Задание 1. Отметьте на числовой окружности точки (-2π),(-) (frac) .

Видео:Как искать точки на тригонометрической окружности.Скачать

Обозначаем числа (frac), (frac), (frac)

Выше мы нашли значения в точках пересечения числовой окружности с осями (x) и (y). Теперь определим положение промежуточных точек. Для начала нанесем точки (frac) , (frac) и (frac) .
(frac) – это половина от (frac) (то есть, (frac) (=) (frac) (:2)) , поэтому расстояние (frac) – это половина четверти окружности.

(frac) – это треть от (π) (иначе говоря, (frac) (=π:3)), поэтому расстояние (frac) – это треть от полукруга.

(frac) – это половина (frac) (ведь (frac) (=) (frac) (:2)) поэтому расстояние (frac) – это половина от расстояния (frac) .

Вот так они расположены друг относительно друга:

Замечание: Расположение точек со значением (0), (frac) ,(π), (frac) , (frac) , (frac) , (frac) лучше просто запомнить. Без них числовая окружность, как компьютер без монитора, вроде бы и полезная штука, а использовать крайне неудобно.

Разные расстояние на окружности наглядно:

Видео:Тригонометрическая окружность. Как выучить?Скачать

Обозначаем числа (frac), (-frac), (frac)

Обозначим на окружности точку (frac) , для этого выполним следующие преобразования: (frac) (=) (frac) (=) (frac) (+) (frac) (=π+) (frac) . Отсюда видно, что от нуля в положительную сторону надо пройти расстояние (π), а потом еще (frac) .

Отметим на окружности точку (-) (frac) . Преобразовываем: (-) (frac) (=-) (frac) (-) (frac) (=-π-) (frac) . Значит надо от (0) пройти в отрицательную сторону расстояние (π) и еще (frac) .

Нанесем точку (frac) , для этого преобразуем (frac) (=) (frac) (=) (frac) (-) (frac) (=2π-) (frac) . Значит, чтобы поставить точку со значением (frac) , надо от точки со значением (2π) пройти в отрицательную сторону расстояние (frac) .

Видео:РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ😉 #shorts #егэ #огэ #математика #профильныйегэСкачать

Обозначаем числа (10π), (-3π), (frac) ,(frac), (-frac), (-frac)

Запишем (10π) в виде (5 cdot 2π). Вспоминаем, что (2π) – это расстояние равное длине окружности, поэтому чтобы отметить точку (10π), нужно от нуля пройти расстояние равное (5) окружностям. Нетрудно догадаться, что мы окажемся снова в точке (0), просто сделаем пять оборотов.

Из этого примера можно сделать вывод:

Числам с разницей в (2πn), где (n∈Z) (то есть (n) — любое целое число) соответствует одна и та же точка.

То есть, чтобы поставить число со значением больше (2π) (или меньше (-2π)), надо выделить из него целое четное количество (π) ((2π), (8π), (-10π)…) и отбросить. Тем самым мы уберем из числа, не влияющие на положение точки «пустые обороты».

Точке, которой соответствует (0), также соответствуют все четные количества (π) ((±2π),(±4π),(±6π)…).

Теперь нанесем на окружность (-3π). (-3π=-π-2π), значит (-3π) и (–π) находятся в одном месте на окружности (так как отличаются на «пустой оборот» в (-2π)).

Кстати, там же будут находиться все нечетные (π).

Точке, которой соответствует (π), также соответствуют все нечетные количества (π) ((±π),(±3π),(±5π)…).

Сейчас обозначим число (frac) . Как обычно, преобразовываем: (frac) (=) (frac) (+) (frac) (=3π+) (frac) (=2π+π+) (frac) . Два пи – отбрасываем, и получается что, для обозначения числа (frac) нужно от нуля в положительную сторону пройти расстояние равное (π+) (frac) (т.е. половину окружности и еще четверть).

Отметим (frac) . Вновь преобразования: (frac) (=) (frac) (=) (frac) (+) (frac) (=5π+) (frac) (=4π+π+) (frac) . Ясно, что от нуля надо пройти расстояние равное (π+) (frac) – и мы найдем место точки (frac) .

Нанесем на окружность число (-) (frac) .
(-) (frac) (= -) (frac) (-) (frac) (=-10π-) (frac) . Значит, место (-) (frac) совпадает с местом числа (-) (frac) .

Обозначим (-) (frac) .
(-) (frac) (=-) (frac) (+) (frac) (=-5π+) (frac) (=-4π-π+) (frac) . Для обозначение (-) (frac) , на числовой окружности надо от точки со значением (–π) пройти в положительную сторону (frac) .

Видео:🔴 ТРИГОНОМЕТРИЯ С НУЛЯ (Тригонометрическая Окружность на ЕГЭ 2024 по математике)Скачать

Число 3п соответствует точке тригонометрической окружности с ординатой ?

Математика | 5 — 9 классы

Число 3п соответствует точке тригонометрической окружности с ординатой ?

С ординатой(0 ; — 1)

чертов минимум на 20 слов.

Видео:Как найти координаты точек на тригонометрической окружностиСкачать

Обозначьте на числовой окружности точку, которая соответствует данному числу : 3пи?

Обозначьте на числовой окружности точку, которая соответствует данному числу : 3пи.

Видео:Тригонометрическая окружность для непонимающихСкачать

На чесловом луче точка А соответствует чётное число какие числа соответствуют точкам В и С — чётные или не чётныеО Е С А В|?

На чесловом луче точка А соответствует чётное число какие числа соответствуют точкам В и С — чётные или не чётные

Видео:ТРИГОНОМЕТРИЧЕСКАЯ ОКРУЖНОСТЬ ЧАСТЬ I #shorts #математика #егэ #огэ #профильныйегэ #окружностьСкачать

На числовой окружности отмечена точка соответствующая числу минус 35 пи деленное на 4?

На числовой окружности отмечена точка соответствующая числу минус 35 пи деленное на 4.

Видео:Тригонометрическая окружностьСкачать

Отметь на числовом луче точку К правее точки В и число, которое ей соответствует и точку М левее точки А и число, которое ей соответствует?

Отметь на числовом луче точку К правее точки В и число, которое ей соответствует и точку М левее точки А и число, которое ей соответствует.

Число 67, точке В — число 72.

Видео:ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ЧИСЛОВОГО АРГУМЕНТАСкачать

Выполнить действия и результат представьте в тригонометрической форме?

Выполнить действия и результат представьте в тригонометрической форме.

Запишите координаты точки, соответствующей числу и постройте вектор, соответствующий числу.

Видео:Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

Кто не знает украинский перевожу : одна из сторон угла совпадает с положительной полуосью абсцисс, а другая пересекает единичную окружность в точке( — 5 / 13 ; — 12, 13)?

Кто не знает украинский перевожу : одна из сторон угла совпадает с положительной полуосью абсцисс, а другая пересекает единичную окружность в точке( — 5 / 13 ; — 12, 13).

Установить соответствие между тригонометрическими функциями и их значениями.

Видео:ТРИГОНОМЕТРИЯ С НУЛЯ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

На рисунке изображена окружность и прямая y = 2x?

На рисунке изображена окружность и прямая y = 2x.

Найдите ординату точки B.

Видео:Вычисление значений тригонометрических функцийСкачать

Найдите на числовой окружности точку, которая соответствует заданному числу : 7П / 2 ; — 3П / 2 ; 9П?

Найдите на числовой окружности точку, которая соответствует заданному числу : 7П / 2 ; — 3П / 2 ; 9П.

Видео:Синус, косинус, тангенс, котангенс за 5 МИНУТСкачать

Точка пи / 12 где находиться на тригонометрической окружности?

Точка пи / 12 где находиться на тригонометрической окружности.

Видео:Тригонометрические функции числового аргумента. Синус, косинус, тангенс, котангенс Тригонометрия #2Скачать

Отношения ординаты точки на окружности к ее абсциссе называется?

Отношения ординаты точки на окружности к ее абсциссе называется.

Если вам необходимо получить ответ на вопрос Число 3п соответствует точке тригонометрической окружности с ординатой ?, относящийся к уровню подготовки учащихся 5 — 9 классов, вы открыли нужную страницу. В категории Математика вы также найдете ответы на похожие вопросы по интересующей теме, с помощью автоматического «умного» поиска. Если после ознакомления со всеми вариантами ответа у вас остались сомнения, или полученная информация не полностью освещает тематику, создайте свой вопрос с помощью кнопки, которая находится вверху страницы, или обсудите вопрос с посетителями этой страницы.

Привет, х * 5 / 6 = 1 х = 1 * 6 / 5 х = 6 / 5 = 1, 2.

16ч — 35 мин = 15 ч 60 мин — 35 мин = 15 ч 25 мин. — выехать 15 ч 25 мин — 3 ч = 12 ч 25 мин. Ответ : собираться начать нужно в 12 часов 25 минут выехать в 15 часов 25 минут.

Го на донбасс поцветочувствительней.

(0, 5 * 64 — 26) * 1, 5 (32 — 26) * 1, 5 6 * 1, 5 = 9 я не несу ответственности за верность решения , переписывая вы берете страх и риск на свою ответственность ).

Диагональ основания — это сторона диагонального сечения ( сечение — прямоугольник) диагональ основания = 312 : 12 = 26 диагональ основания — это гипотенуза прямоугольного треугольника с катетами , равными сторонам основания ( х и у) х² + у² = 676 ху ..

1)48 * 5 = 240(км) — расстояние между городами 2)240 : 6 = 40(км / ч) — скорость на обратном пути 3)48 — 40 = 8(км / ч) — меньше Ответ : на 8 км / ч скорость машины на обратном пути была меньше.

350 * 20 100 = 70 350 + 70 = 420.

350 : 100 * 20 = 70 (руб. ) — 20% 350 + 70 = 420 (руб. ) — придется платить ежемесячно. Ответ : 420 рублей.

34 — 16 = 18 всё понятно или ещё лучше разяснить.

Видео:Алгебра 10 класс. 2 октября. Тангенс и котангенс на окружностиСкачать

Тригонометрический круг: вся тригонометрия на одном рисунке

Тригонометрический круг — это самый простой способ начать осваивать тригонометрию. Он легко запоминается, и на нём есть всё необходимое.
Тригонометрический круг заменяет десяток таблиц.

Вот что мы видим на этом рисунке:

Видео:Числовая окружность | Алгебра 10 класс #8 | ИнфоурокСкачать

А теперь подробно о тригонометрическом круге:

Нарисована единичная окружность — то есть окружность с радиусом, равным единице, и с центром в начале системы координат. Той самой системы координат с осями и , в которой мы привыкли рисовать графики функций.

Мы отсчитываем углы от положительного направления оси против часовой стрелки.

Полный круг — градусов.
Точка с координатами соответствует углу ноль градусов. Точка с координатами отвечает углу в , точка с координатами — углу в . Каждому углу от нуля до градусов соответствует точка на единичной окружности.

Косинусом угла называется абсцисса (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .

Синусом угла называется ордината (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .

Всё это легко увидеть на нашем рисунке.

Итак, косинус и синус — координаты точки на единичной окружности, соответствующей данному углу. Косинус — абсцисса , синус — ордината . Поскольку окружность единичная, для любого угла и синус, и косинус находятся в пределах от до :

Простым следствием теоремы Пифагора является основное тригонометрическое тождество:

Для того, чтобы узнать знаки синуса и косинуса какого-либо угла, не нужно рисовать отдельных таблиц. Всё уже нарисовано! Находим на нашей окружности точку, соответствующую данному углу , смотрим, положительны или отрицательны ее координаты по (это косинус угла ) и по (это синус угла ).

Принято использовать две единицы измерения углов: градусы и радианы. Перевести градусы в радианы просто: градусов, то есть полный круг, соответствует радиан. На нашем рисунке подписаны и градусы, и радианы.

Если отсчитывать угол от нуля против часовой стрелки — он положительный. Если отсчитывать по часовой стрелке — угол будет отрицательным. Например, угол — это угол величиной в , который отложили от положительного направления оси по часовой стрелке.

Легко заметить, что

Углы могут быть и больше градусов. Например, угол — это два полных оборота по часовой стрелке и еще . Поскольку, сделав несколько полных оборотов по окружности, мы возвращаемся в ту же точку с теми же координатами по и по , значения синуса и косинуса повторяются через . То есть:

где — целое число. То же самое можно записать в радианах:

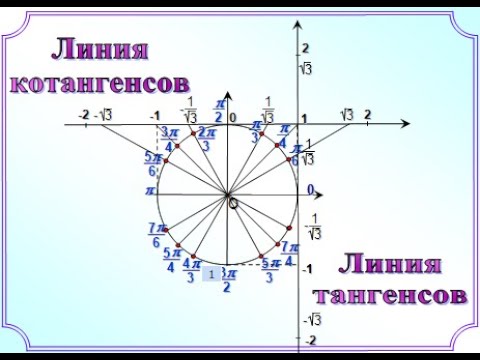
Можно на том же рисунке изобразить ещё и оси тангенсов и котангенсов, но проще посчитать их значения. По определению,

📹 Видео

6 Линия тангенсов и линия котангенсовСкачать

Алгебра 10 класс Поворот точки вокруг начала координат ЛекцияСкачать

ТРИГОНОМЕТРИЯ с нуля за 30 минутСкачать