Четырехугольник klmn описан вокруг окружности kl 23

Видео:9 класс, 23 урок, Окружность, вписанная в правильный многоугольникСкачать

Четырехугольник klmn описан возле окружности kl

Четырехугольник KLMN описан около окружности и вписан в окружность. Прямые KL и NM пересекаются в точке P. Найдите площадь треугольника KPN, если известно, что ∠KPN = φ и радиусы окружностей, вписанных в треугольники KPN и LMP равны соответственно r и R.

Решение . Первый случай.

Центры O₁ и O окружностей, вписанных в треугольники KPN и LMP соответственно, лежат на биссектрисе PO угла KPN. Окружность, вписанная в четырехугольник KLMN, является также окружностью, вписанной в треугольник KPN и вневписанной окружностью треугольника LMP.

Четырехугольник KLMN вписан в окружность, следовательно, ∠LKN + ∠LMN = 180°. Но ∠LMP + ∠LMN = 180°, откуда ∠LKN = ∠LMP. Так как треугольники KPN и LMP имеют еще общий угол KPN, они подобны, причем коэффициент подобия равен отношению радиусов окружностей, вписанных в эти треугольники.

1)

2) S_ΔLPM = pR, где p — полупериметр треугольника LPM равный длине отрезка AP, как сумма отрезков касательных проведенных из одной точки.

3) из прямоугольного треугольника OAP находим откуда

Подставляя найденное S_ΔLPM в формулу площади треугольника KPN, окончательно получаем

Отличается от первого расположением точки P левее точек N и K. В этом случае R > r и в рассуждении они и треугольники LMP и KPN должны быть поменяны местами. Таким образом, в этом случае KPN — меньший из двух треугольников, а радиус вписанной в него окружности r. Значит

S_KPN = rp, где p — полупериметр треугольника KPN равный отрезку PB. При этом, как и в первом случае, Таким образом,

Ответ: или

Видео:Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

Четырехугольник KLMN вписан в окружность, его диагонали KM и LN пересекаются в точке F, причем KL=8, MN=4, периметр треугольника MNF

Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Ваш ответ

Видео:Урок 2. Описанная окружность около четырехугольника. Задача из ОГЭ| Подобные треугольникиСкачать

решение вопроса

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Похожие вопросы

• Все категории
• экономические 43,277
• гуманитарные 33,618
• юридические 17,900
• школьный раздел 606,882
• разное 16,829

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:8 класс Геометрия. Окружность вписанная в четырехугольник и описанная около четырехугольника Урок #4Скачать

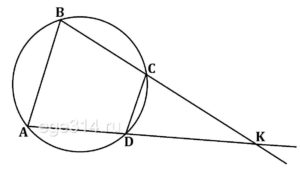
Решение №1222 Известно, что около четырехугольника АВСD можно описать окружность и что продолжения сторон АD и ВС …

Известно, что около четырехугольника АВСD можно описать окружность и что продолжения сторон АD и ВС четырёхугольника пересекаются в точке К. Докажите, что треугольники КАВ и КСD подобны.

Источник: ОГЭ Ященко 2021 (36 вар)

В ΔКАВ и ΔКСD ∠К общий.
Четырёхугольник АВСD вписан в окружность сумма противоположных углов равна 180°:

∠ABC + ∠ADC = 180º
∠ABC = 180º – ∠ADC

∠ADC и ∠СDK смежные их сумма равна 180º:

∠ADC + ∠СDK = 180º
∠СDK = 180º – ∠ADC

Из этих двух равенств получаем:

∠ABC = ∠СDK

Тогда ΔКАВ и ΔКСD подобны по двум равным углам.
Что и требовалось доказать.

Видео:3 правила для вписанного четырехугольника #shortsСкачать

Около четырехугольника KLMN описана окружность. Найдите уголMLN,если LM=MN и угол LKN=40 градусам

Четырехугольник КЛМН, ЛМ=МН, уголЛКН=40, проводим КМ, равные хорды стягивают равные дуги, дуга ЛМ=дуга МН, уголЛКН-вписанный=1/2дуге ЛН, дуга ЛН=2*уголЛКН=2*40=80, КМ-биссектриса, дуга ЛМ=дуга МН=дуга ЛН/2=80/2=40, уголМЛН — вписанный=1/2 дуге МН=40/2=20

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Другие вопросы из категории

На прямой отмечены три точки.При этом образовалось три отрезка два из которых равны 24 см и 9 см.Какой может быть длина третьего отрезка.

равно 16 см. Найдите угол AOB.

Одна из диагоналей ромба на 4 см больше другой, площадь ромба=96
найти стороны

Видео:9 класс, 22 урок, Окружность, описанная около правильного многоугольникаСкачать

Читайте также

ЕАС, если Е — точка на окружности, АС — диаметр, угол ЕСА = 35 градусов (Если можно, отправьте как нибудть рисунок) и объясните как тут его вставить можно)

параллелограм можно вписаать окружность, то этот параллелограм-ромб. 4.Если около параллелограмма можно описать окружность, то этот параллелограм-прямоугольник. 5.Если в трапецию можно вписать окружность, то эта трапеция-равнобедренная.

Около четырехугольника ABCD описана окружность. Найдите угол ВАС, если ВС = CD и угол BDC равен 150 .

б) АВ=13 см, ВС=7 см, угол В=60 градусам

2. НАйдите неизвестную сторону треугольника MNP, если:

а) MN=7 см, MP=15 см, угол M=120 градусам;

б) MN=5 см, MP=14 см, угол N=120 градусам.

3. В параллелограмме острый угол равен 60 градусам, а стороны равны 6 см и 8 см. Найдите:

а) меньшую диагональ (ВD);

б) большую диагональ (АС)

4. Найдите косинусы углов параллелограмма, если:

а) его стороны равны 8 мм и 10 мм, а одна из диагоналей равна 14 мм;

б) его стороны равны 12 дм и 14 дм, а одна из диагоналей равна 20 дм.

5. Найдите стороны параллелограмма, если с его большей диагональю, равной 25 см, они образуют углы 20 и 60 градусов.

6. В треугольнике АВС дано: АВ=16 см, угол В=40 градусов, угол А=30 градусам. Найдите угол С, стороны АС и ВС, радиус описанной окружности.

7. Докажите, что в биссектриса AD треугольника АВС делит сторону ВС на отрезки, пропорциональные сторонам АВ и АС. (Указание. Примените теорему синусов к треугольникам АВD и АDС)

8. Докажите, что в параллелограмме сумма квадратов диагоналей равна сумме квадратов сторон (Указание. Найдите квадраты диагоналей, используя теорему косинусов)

9. В параллелограмме острый угол между диагоналями 60 градусов одна из сторон 6 см, меньшая диагональ 8 см. Найти:

а) большую диагональ;

б) вторую сторону параллелограмма

10. Укажите вид треугольника, не вычисляя его углов, если:

11. Угол при основании равнобедренного треугольника равен равен 30 градусам, а боковая сторона равна 14 см. Найти:

а) медиану, проведенную к высоте

б) биссектрису угла при основании

12. Стороны треугольника равны 24 см, 18 см и 8 см. Найти:

а) больший угол треугольника

б) меньший угол треугольника

13. В треугольнике АВС известны стороны: Ас=6 см, ВС=9 см, АВ=10 см. Найти высоту, проведённую к стороне АВ. (Указание. Воспользуйтесь следствием из теоремы косинусов)

🎬 Видео

16) Четырехугольник АВСD описан около окружности, AD=7, DC=12, BC=13. Найдите AB. Математика огэ.Скачать

Вписанные четырехугольники. 9 класс.Скачать

Четырехугольники, вписанные в окружность. 9 класс.Скачать

ОПИСАННЫЕ И ВПИСАННЫЕ ОКРУЖНОСТИ ЧЕТЫРЕХУГОЛЬНИКА . §10 геометрия 8 классСкачать

Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Вписанная и описанная окружности | Лайфхак для запоминанияСкачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

11 класс, 43 урок, Вписанный четырехугольникСкачать

Построить описанную окружность (Задача 1)Скачать

Окружность №16 из ОГЭ. Вписанные и описанные многоугольники. Квадрат и окружность.Скачать

Описанная и вписанная окружности четырехугольника - 8 класс геометрияСкачать