Через любые две точки можно провести только одну окружность (4 видео)

Через любые две точки можно провести только одну окружность

Выберите верные утверждения и запишите в ответе их номера.

1) Через любые две различные точки плоскости можно провести не более одной окружности.

2) Если при пересечении двух данных прямых третьей внутренние накрест лежащие углы равны, то данные прямые параллельны.

3) Все углы прямоугольника равны.

Проверим каждое из утверждений.

1) Неверно, поскольку через две различные точки плоскости можно провести одну, две и более окружностей.

2) Верно, по признаку параллельных прямых.

3) Верно, все углы прямоугольника равны 90°.

Содержание

Окружность и круг
теория по математике 📈 планиметрия
Определения
Свойство хорд
Длина окружности
Дуга, касательная, круг, сектор, сегмент
Свойства касательной
Сколько всего аксиом в геометрии? если не тяжело напишите мне их пожалуеста! запамятовал вот нужна ваша помощь
🎦 Видео

Видео:№8. Верно ли утверждение: а) если две точки окружности лежат в плоскостиСкачать

Окружность и круг

теория по математике 📈 планиметрия

Определения

Окружность – множество всех точек плоскости, равноудаленных от одной данной точки (центра окружности). Другими словами – это замкнутая линия, длину которой можно измерить.

На рисунке центр окружности обозначен точкой О. 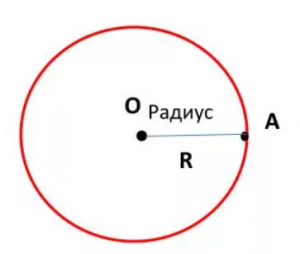Определения

Радиус – расстояние от центра до любой точки окружности. На рисунке радиус обозначен АО. Все радиусы одной окружности равны. Радиус можно обозначать латинскими буквами R или r.

Диаметр – отрезок, который соединяет две точки окружности и проходит через её центр. На рисунке диаметр обозначен АВ. Все диаметры одной окружности равны. В одном диаметре содержится два радиуса. Диаметр обозначается буквой d.

Хорда — длинный эластичный продольный тяж у хордовых животных; осевой скелет их предковых и некоторых современных форм. Тянется вдоль тела ниже центральной нервной системы и выше полости тела.

Свойство хорд

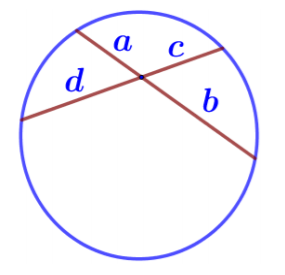
Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды. Так, на рисунке показаны две пересекающиеся хорды, одна состоит из отрезков a и b, вторая из отрезков d и с, следовательно, ab=dс.

Длина окружности

Длину окружности можно вычислить по формуле:

C=2πR, где π=3,14.

Дуга – часть окружности, которая соединяет две точки. На рисунке мы видим несколько дуг, например, дуги CD (малая и большая). Дуга АВ – называется полуокружностью, так как стягивает концы диаметра. Обозначается дуга значком ∪АВ.

Видео:Окружность. 7 класс.Скачать

Дуга, касательная, круг, сектор, сегмент

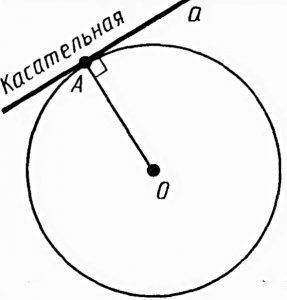
Из точки, не лежащей на окружности можно провести касательную – прямую, которая имеет с окружностью только одну общую точку (рисунок 4).

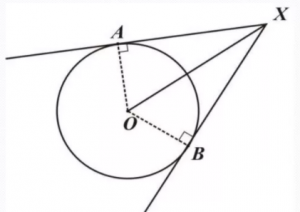
Свойства касательной

На рисунке видно, что АХ=ВХ, угол АХО равен углу ВХО.

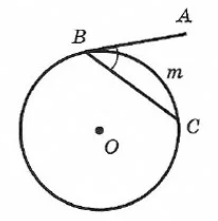
Угол АВС (образован касательной АВ и хордой ВС) равен половине дуги m.

Круг – часть плоскости, ограниченная окружностью. Другими словами, круг – это всё, что находится внутри окружности.

Площадь круга вычисляется по формуле:

S=πR 2 , где π=3,14.

Сектор и его площадь

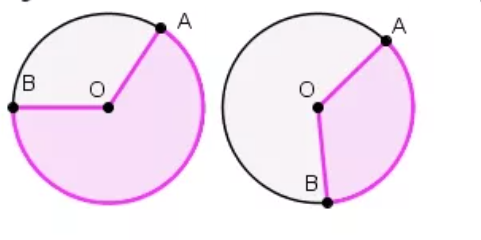
Сектор – область круга, ограниченная двумя радиусами. На рисунке сектор выделен сиреневым цветом, он ограничен радиусами ОА и ОВ.

Площадь кругового сектора вычисляется по формуле:

S= π R 2 360 . . × α , где α – угол между радиусами.

Сегмент – это область круга, ограниченная хордой и дугой. На рисунке сегмент выделен сиреневым цветом. Также можно сказать, что это часть круга, отсекаемая от него хордой. На рисунке видно, как

Видео:10 класс, 3 урок, Некоторые следствия из аксиомСкачать

Сколько всего аксиом в геометрии? если не тяжело напишите мне их пожалуеста! запамятовал вот нужна ваша помощь

В Евклидовой — пять.
В «Началах» Евклида была дана следующая аксиоматика:
1. От всякой точки до всякой точки можно провести прямую.
2. Ограниченную прямую можно непрерывно продолжать по прямой.
3. Из всякого центра всяким раствором может быть описан круг.
4. Все прямые углы равны между собой.
5. Если прямая, пересекающая две прямые, образует внутренние односторонние углы, меньшие двух прямых, то, продолженные неограниченно, эти две прямые встретятся с той стороны, где углы меньше двух прямых.
Существуют и другие аксиоматики.. . Но если ты и этой не знаешь, то другие тебе лишние.. .

Евклид в своих «Началах» описал пять аксиом:
1. Через каждые две точки можно провести ровно одну прямую;
2. Вдоль любого отрезка можно провести прямую;
3. Имея отрезок, можно провести окружность так, что отрезок — радиус, а один из его концов — центр окружности;
4. Все прямые углы равны.
5. Аксиома параллельности Евклида: Через точку А вне прямой а в плоскости, проходящей через А и а, можно провести лишь одну прямую, не пересекающую а.

А вот в учебнике по геометрии за 7-11 классы А. Погорелова их девять:
1. Какова бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей. Через любые две точки можно провести прямую, и только одну;
2. Из трех точек на прямой одна и только одна лежит между двумя другими;
3. Каждый отрезок имеет определенную длину, большую нуля. Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой.
4. Прямая разбивает плоскость на две полуплоскости.
5. Каждый угол имеет определенную градусную меру, большую нуля. Развернутый угол равен 180 градусам. Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами.
6. На любой полупрямой от ее начальной точки можно отложить отрезок заданной длины, и только один.
7. От любой полупрямой в заданную полуплоскость можно отложить угол с заданной градусной мерой, меньшей 180 градосов, и только один.
8. Каков бы ни был треугольник, существует равный ему треугольник в заданном расположении относительно данной полупрямой.
9. Через точку, не лежащую на данной прямой, можно провести на плоскости не более одной прямой, параллельной данной.