Через 2 параллельные прямые проходит плоскость и притом только одна верно или (4 видео)

Введение в стереометрию. Параллельность

Важные аксиомы стереометрии

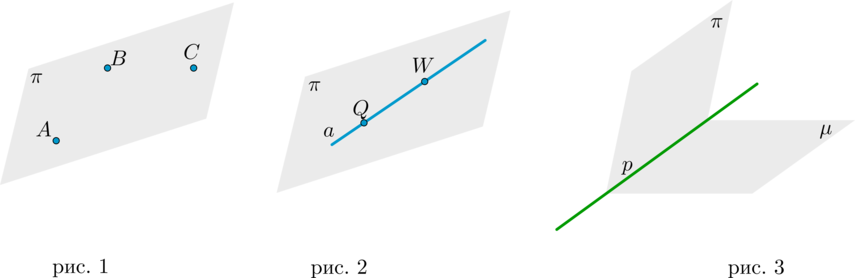
1. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.
Таким образом, любая плоскость однозначно задается тремя точками, не лежащими на одной прямой: (pi=(ABC)) (рис. 1).

2. Если две точки прямой лежат в некоторой плоскости, то и вся прямая лежит в этой плоскости: (ain pi) .
Говорят также, что плоскость содержит прямую: (pisubset a) (рис. 2).

3. Если две плоскости имеют общую точку, то они имеют и общую прямую, на которой лежат все общие точки этих плоскостей.
Таким образом, если плоскости пересекаются, то они пересекаются по прямой: (picap mu=p) .
Данная прямая (p) называется линией пересечения плоскостей (рис. 3).

Заметим, что плоскость обычно изображают в виде внутренности параллелограмма. Почему? Посмотрите, например, сбоку на стол. В виде какой фигуры выглядит столешница?

Следствия из аксиом

1. Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна (рис. 4).

2. Через две пересекающиеся прямые проходит плоскость, и притом только одна (рис. 5).

Доказательство

1. Действительно, отметим на прямой (a) некоторые две точки (A) и (B) . Тогда мы получим три точки (A, B, C) , не лежащие на одной прямой. Через них можно провести единственную плоскость (pi) . А т.к. две выбранные точки (A) и (B) прямой лежат в этой плоскости, то и вся прямая лежит в этой плоскости.

2. Действительно, пусть (O) – точка пересечения данных прямых (p) и (q) . Отметим еще по одной точке (P) и (Q) на каждой прямой (отличающиеся от точки (O) ). Получили три точки (P, Q, O) , не лежащие на одной прямой. Через них проходит единственная плоскость (pi) . А т.к. две точки каждой прямой лежат в этой плоскости, то и все точки каждой прямой будут лежать в этой плоскости.

Определения

Две прямые в пространстве параллельны, если они лежат в одной плоскости и не пересекаются.

Следствие 1

Через две параллельные прямые проходит плоскость, и притом только одна.

Теорема 1

Через любую точку (A) в пространстве, не лежащую на данной прямой (b) , проходит прямая (a) , параллельная данной, и притом только одна.

Доказательство

Через точку (A) и прямую (b) можно провести единственную плоскость (по аксиоме); пусть эта плоскость называется (pi) . Прямая (a) , параллельная прямой (b) , должна лежать с ней в одной плоскости, а также должна проходить через точку (A) , следовательно, должна лежать в плоскости (pi) . Но в плоскости через точку, не лежащую на прямой, можно провести ровно одну прямую, параллельную данной (теорема планиметрии), чтд.

Теорема 2

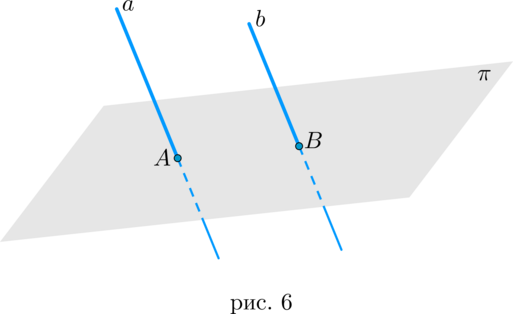
Если одна из двух параллельных прямых пересекает плоскость, то и другая прямая пересекает эту плоскость.

Доказательство

Пусть (aparallel b) и (acap pi=A) . Докажем, что и (b) пересечет плоскость (pi) (назовем их точку пересечения (B) ).

Проведем через прямые (a) и (b) плоскость (mu) (это возможно в силу определения параллельных прямых). Тогда плоскости (pi) и (mu) имеют общую точку (A) , следовательно, имеют и общую прямую (p) , на которой лежат все их общие точки. Но т.к. (bparallel a) и (acap p=A) , то прямая (b) тоже пересекает прямую (p) . Значит, прямая (b) пересекает и плоскость (mu) (это и есть точка (B) ).

Теорема 3: о параллельности трех прямых

Если прямая (a) параллельна прямой (b) , а та в свою очередь параллельна прямой (c) , то (aparallel c) .

Доказательство

1) Отметим некоторую точку (C) на прямой (c) и проведем плоскость (pi) через прямую (a) и точку (C) . Прямая (c) будет лежать в этой плоскости. Действительно, т.к. прямая (c) и плоскость (pi) имеют общую точку (C) , то в противном случае прямая (c) будет пересекать эту плоскость. Но т.к. (bparallel c) , то и прямая (b) будет пересекать (pi) ; а т.к. (aparallel b) , то и прямая (a) будет пересекать эту плоскость. А это противоречит нашему построению.

2) Теперь прямые (a) и (c) лежат в одной плоскости, значит, они могут либо пересекаться, либо быть параллельны. Предположим, что (c) пересекает (a) в точке (A) . Тогда получается, что через точку (A) проведены две прямые, параллельные прямой (b) , что противоречит теореме 1.

Определение

Существует три вида взаимного расположения прямой и плоскости:

1. прямая имеет с плоскостью две общие точки (то есть лежит в плоскости) — рис. 4;

2. прямая имеет с плоскостью ровно одну общую точку (то есть пересекает плоскость) — рис. 6;

3. прямая не имеет с плоскостью общих точек (то есть параллельна плоскости).

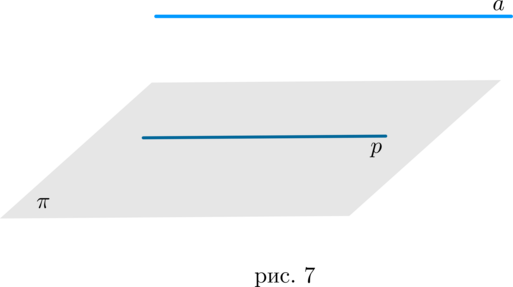
Теорема 4: признак параллельности прямой и плоскости

Если прямая (a) , не лежащая в плоскости (pi) , параллельна некоторой прямой (p) , лежащей в плоскости (pi) , то она параллельна данной плоскости (рис. 7).

Доказательство

Докажем, что прямая (a) не может пересекать плоскость (pi) (случай, что прямая лежит в плоскости, невозможен по условию). Предположим, что это не так. Во-первых, проведем плоскость (mu) через прямые (a) и (p) (значит, плоскости (pi) и (mu) пересекаются по прямой (p) ). Во-вторых, пусть (acappi=A) . Т.к. (aparallel p) , то точка (A) не может лежать на прямой (p) . Значит, плоскости (pi) и (mu) имеют еще одну общую точку (A) , не лежащую на их линии пересечения, что противоречит аксиоме 3. Чтд.

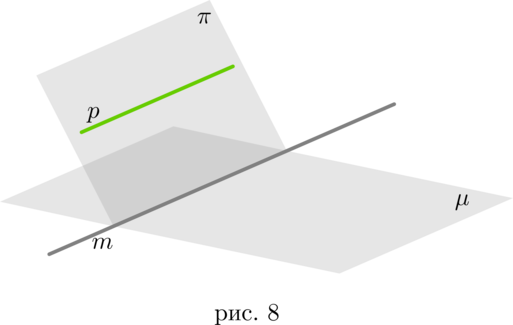
Следствие 2

Пусть прямая (p) параллельна плоскости (mu) . Если плоскость (pi) проходит через прямую (p) и пересекает плоскость (mu) , то линия пересечения плоскостей (pi) и (mu) — прямая (m) — параллельна прямой (p) (рис. 8).

Доказательство

Т.к. прямые (m) и (p) лежат в одной плоскости (pi) , то они могут быть либо параллельны, либо пересекаться, либо совпадать. Совпадать они не могут, потому что тогда (pin mu) , а это противоречит условию. Если (mcap p=O) , то (p) пересекает плоскость (mu) в точке (O) , что опять же противоречит условию. Значит, (mparallel p) .

Следствие 3

Если прямые (a) и (b) параллельны и прямая (a) также параллельна плоскости (alpha) , то и прямая (b) либо параллельна, либо лежит в плоскости (alpha) .

Определение

Существует три типа взаимного расположения плоскостей в пространстве: совпадают (имеют три общие точки, не лежащие на одной прямой), пересекаются (имеют общие точки, лежащие строго на одной прямой), и не имеют общих точек.

Если две плоскости не имеют общих точек, то они называются параллельными плоскостями.

Теорема 5: признак параллельности плоскостей

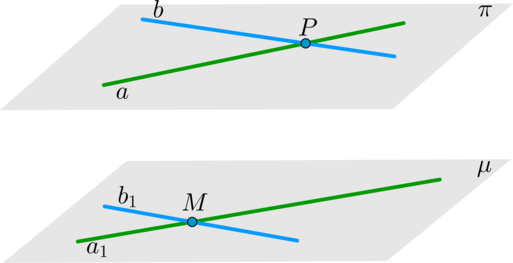
Если две пересекающиеся прямых из одной плоскости параллельны двум пересекающимся прямым из другой плоскости, то такие плоскости будут параллельны.

Доказательство

Рассмотрим две плоскости (pi) и (mu) и в них пересекающиеся прямые (a, b) и (a_1, b_1) соответственно, такие что (aparallel a_1, bparallel b_1) . Докажем, что плоскости не имеют общих точек.

Предположим, что это не так. Пусть плоскости имеют общую точку, значит они имеют и общую прямую (y) : (picap mu=y) . Данная прямая не может быть параллельна обеим прямым (a) и (b) (т.к. они все лежат в одной плоскости (pi) ), значит, хотя бы одну из этих прямых она пересекает. Пусть это будет прямая (a) , то есть (acap y=Y) . Т.к. прямая (y) лежит и в плоскости (mu) , то (Yin mu) , то есть прямая (a) имеет с плоскостью (mu) общую точку (Y) . Но это невозможно, т.к. по признаку параллельности прямой и плоскости прямая (a) параллельна плоскости (mu) . Чтд.

Следствие 4

Если две параллельные плоскости (alpha) и (beta) пересечены третьей плоскостью (gamma) , то линии пересечения плоскостей также параллельны:

[alphaparallel beta, alphacap gamma=a, betacapgamma=b Longrightarrow aparallel b]

Следствие 5

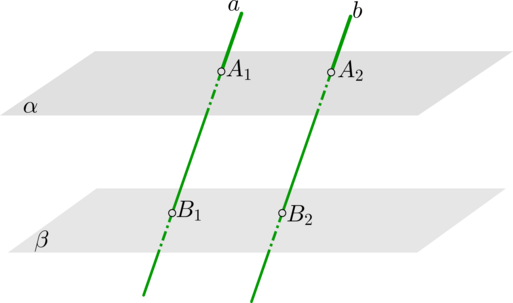
Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны:

[alphaparallel beta, aparallel b Longrightarrow A_1B_1=A_2B_2]

Видео:Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

Параллельные прямые в пространстве. Параллельность трех прямых

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

На этом уроке мы дадим основные определения и теоремы на тему параллельных прямых в пространстве.
В начале урока рассмотрим определение параллельных прямых в пространстве и докажем теорему о том, что через любую точку пространства можно провести только одну прямую, параллельную данной. Далее докажем лемму о двух параллельных прямых, пересекающих плоскость. И с ее помощью докажем теорему о двух прямых, параллельных третьей прямой.

Видео:10 класс, 4 урок, Параллельные прямые в пространствеСкачать

Тест по теме: «Аксиомы стереометрии и некоторые следствия из них»

тест по теме: «Аксиомы стереометрии

и некоторые следствия из них»

1. Какое утверждение неверное?

1) Через любые три точки проходит плоскость, и притом только одна.

2) Через две пересекающиеся прямые проходит плоскость, и притом только одна.

3) Через две параллельные прямые проходит плоскость, и притом только одна.

2. Параллелограмм ABCD лежит в плоскости , если…

3. ABCDA1B1C1D1 – куб. Тогда плоскости (ABC) и (DD1C1)…

2) не пересекаются;

4. Прямая MN не пересекает плоскость…

5. SABCD – четырёхугольная пирамида. Прямая SD не пересекает прямую…

6. Две различные плоскости не могут иметь…

3) три общих точки, не лежащие на одной прямой.

7. Какое утверждение неверное?

8. Через прямые m и k можно провести более одной плоскости. Тогда прямые m и k…

9. Точка А принадлежит прямой а. Тогда через них можно провести…

1) хотя бы одну плоскость;

2) только одну плоскость;

3) не более одной плоскости.

1) любые три точки лежат в одной плоскости;

2) любые четыре точки не лежат в одной плоскости;

3) через любые три точки, не лежащие на одной прямой, проходит плоскость, и при том только одна.

2. AB и CD – диаметры окружности с центром O. Все точки окружности лежат в плоскости, если…

3. Верно ли, что прямая лежит в плоскости данного треугольника, если она…

1) пересекает две стороны треугольника;

2) проходит через одну из вершин треугольника;

3) содержит одну из сторон треугольника.

4. ABCDA1B1C1D1 – куб. Тогда плоскости (AB1C1) и (СDD1)…

2) не пересекаются;

5. Прямая MN не пересекает плоскость…

6. DABC – треугольная пирамида. Прямая BD не пересекает прямую…

7. Сколько общих точек, не лежащих на одной прямой, не могут иметь две различные плоскости?

8. Даны две параллельные прямые a и b и точка M, не лежащая ни на одной из них. Точка M лежит в одной плоскости с прямыми a и b, если через точку M можно провести прямую, пересекающую…

1) хотя бы одну из данных прямых;

2) только одну из данных прямых;

3) две данные прямые.

9. Через три точки A, B и C можно провести единственную плоскость. Тогда точки…