Чему равен центральный угол опирающийся на дугу 57 в окружности

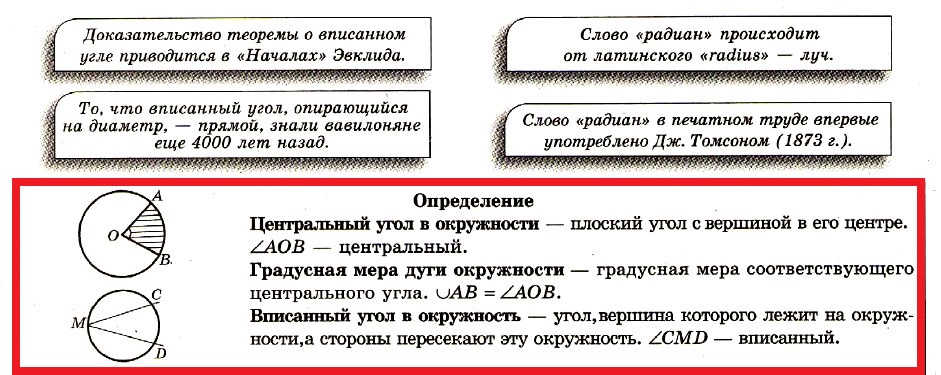
Центральный угол в окружности — плоский угол с вершиной в его центре.
Градусная мера дуги окружности — градусная мера соответствующего центрального угла.
Вписанный угол в окружность — угол, вершина которого лежит на окружности^ стороны пересекают эту окружность.

Доказательство теоремы о вписанном угле приводится в «Началах» Эвклида. То, что вписанный угол, опирающийся на диаметр, — прямой, знали вавилоняне еще 4000 лет назад.

Свойства вписанного угла. Радианная мера углов

Свойства вписанного угла:
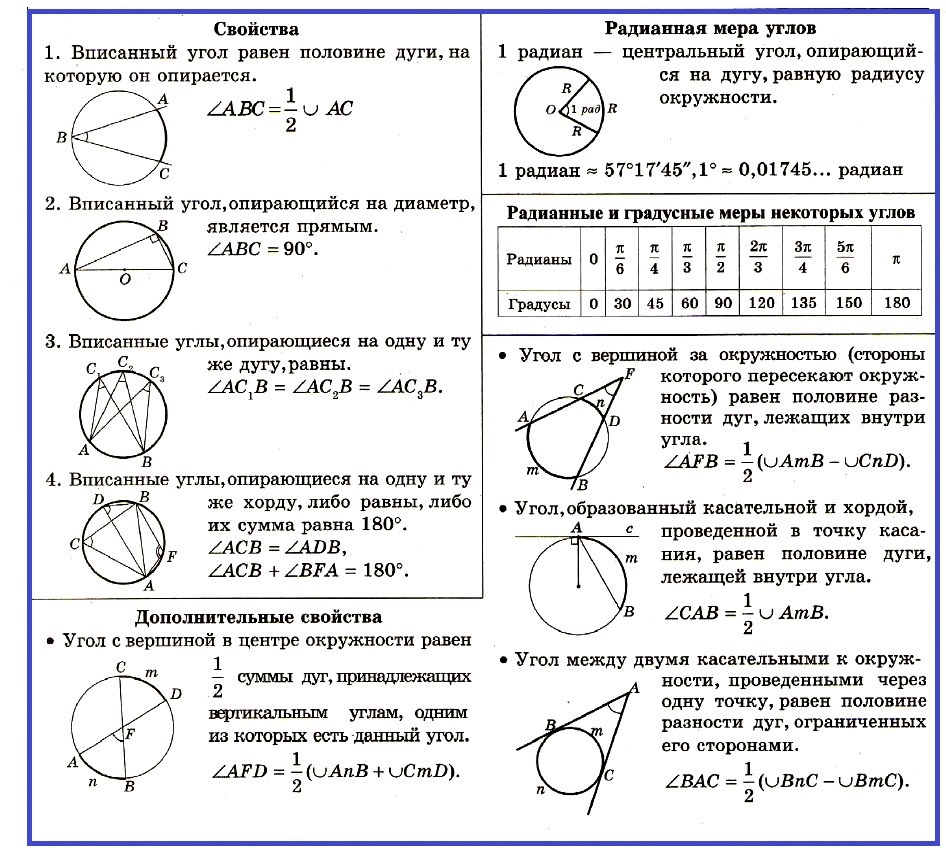
1. Вписанный угoл равен половине дуги, на которую он опирается.
2. Вписанный угoл, опирающийся на диаметр, является прямым.
3. Вписaнные углы, опирающиеся на одну и ту же дугу, равны.
4. Вписaнные углы, опирающиеся на одну и ту же хорду, либо равны, либо их сумма равна 180°.

Радианная мера углов
1 радиан — центральный угол, опирающийся на дугу, равную радиусу окружности. 1 радиан = примерно 57°.
• Угол с вершиной за окружностью (стороны которого пересекают окружность) равен половине разности дуг, лежащих внутри угла.
• Угол,образованный касательной и хордой, с проведенной в точку касания, равен половине дуги, лежащей внутри угла.
• Угол между двумя касательными к окружности, проведенными через одну точку, равен половине разности дуг, ограниченных его сторонами.

Это конспект по теме «Центральный угол. Вписанный угол». Выберите дальнейшие действия:

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Углы в окружности, центральный и вписанный. Свойства и способы нахождения

Планиметрия – это раздел геометрии, изучающий свойства плоских фигур. К ним относятся не только всем известные треугольники, квадраты, прямоугольники, но и прямые и углы. В планиметрии также существуют такие понятия, как углы в окружности: центральный и вписанный. Но что они означают?

Видео:Длина дуги окружности. 9 класс.Скачать

Что такое центральный угол?

Для того чтобы понять, что такое центральный угол, нужно дать определение окружности. Окружность – это совокупность всех точек, равноудаленных от данной точки (центра окружности).

Очень важно отличать ее от круга. Нужно запомнить, что окружность – это замкнутая линия, а круг – это часть плоскости, ограниченная ею. В окружность может быть вписан многоугольник или угол.

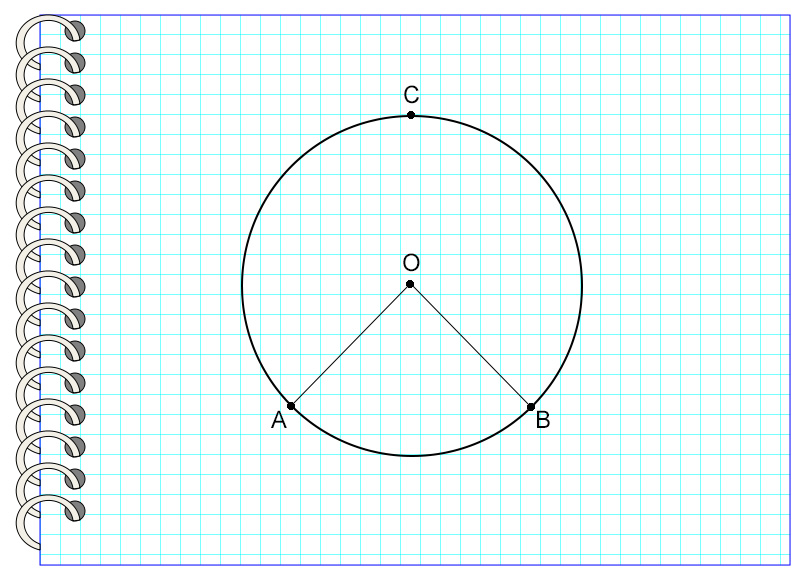
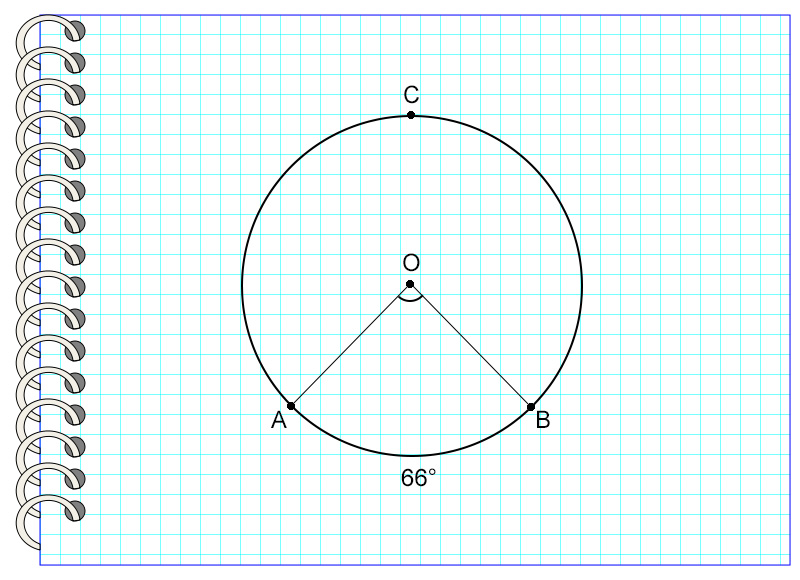
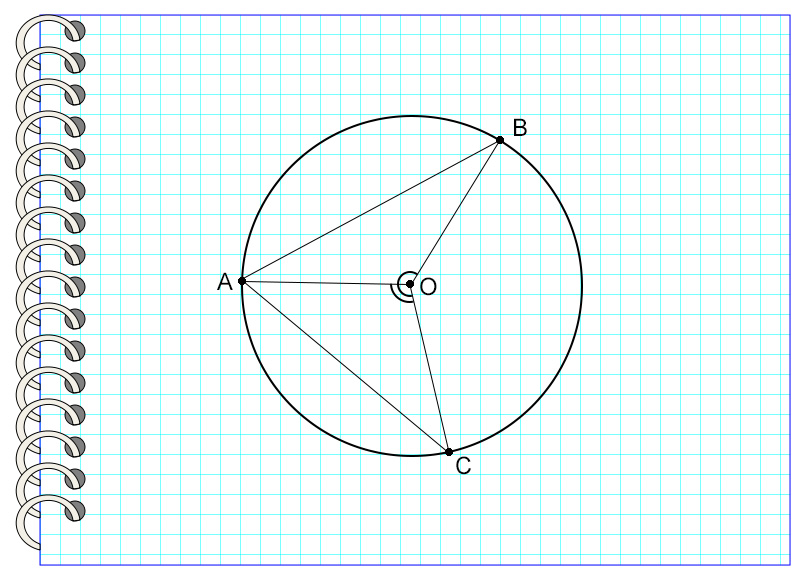
Центральный угол – это такой угол, вершина которого совпадает с центром окружности, а стороны пересекают окружность в двух точках. Дуга, которую угол ограничивает точками пересечения, называется дугой, на которую опирается данный угол.

Рассмотрим пример №1.

На картинке угол AOB – центральный, потому что вершина угла и центр окружности – это одна точка О. Он опирается на дугу AB, не содержащую точку С.

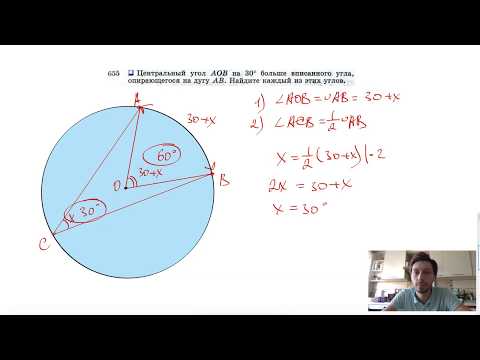
Видео:№655. Центральный угол АОВ на 30° больше вписанного угла, опирающегося на дугу АВ. НайдитеСкачать

Чем вписанный угол отличается от центрального?

Однако кроме центральных существуют также вписанные углы. В чем же их различие? Так же как и центральный, вписанный в окружность угол опирается на определенную дугу. Но его вершина не совпадает с центром окружности, а лежит на ней.

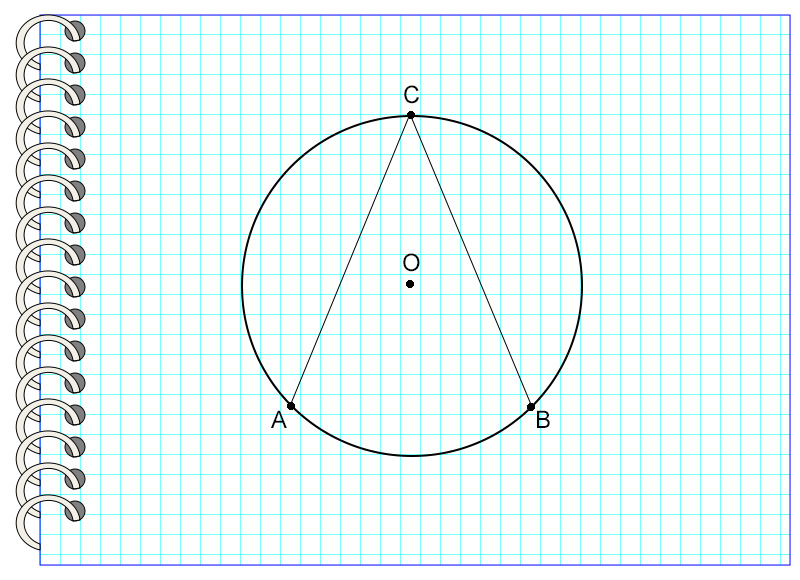
Приведем следующий пример.

Угол ACB называется углом, вписанным в окружность с центром в точке О. Точка С принадлежит окружности, то есть лежит на ней. Угол опирается на дугу АВ.

Видео:Вписанные углы в окружностиСкачать

Чему равен центральный угол

Для того чтобы успешно справляться с задачами по геометрии, недостаточно уметь различать вписанный и центральный углы. Как правило, для их решения нужно точно знать, как найти центральный угол в окружности, и уметь вычислить его значение в градусах.

Итак, центральный угол равен градусной мере дуги, на которую он опирается.

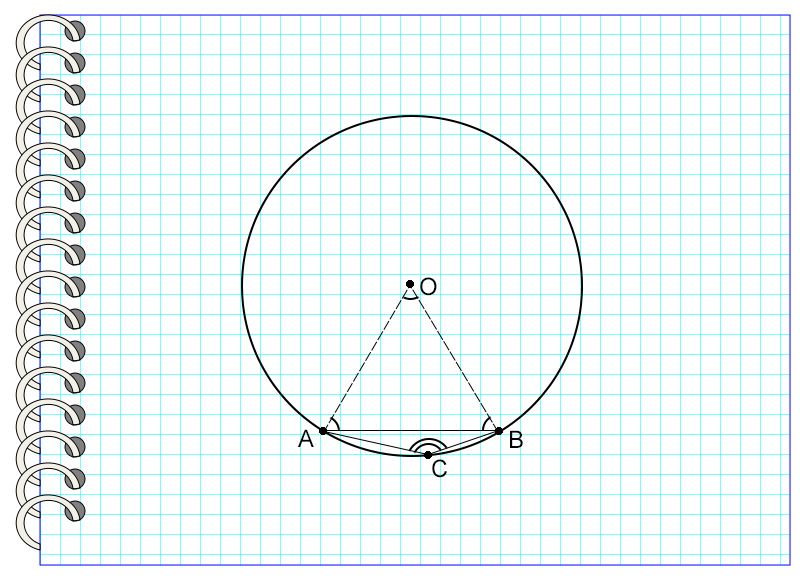
На картинке угол АОВ опирается на дугу АВ, равную 66°. Значит, угол АОВ также равен 66°.

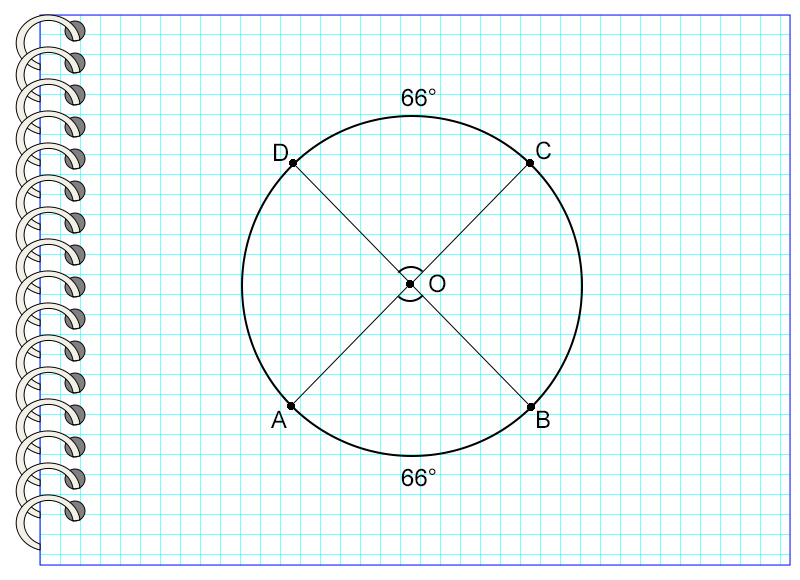
Таким образом, центральные углы, опирающиеся на равные дуги, равны.

На рисунке дуга DC равна дуге AB. Значит, угол АОВ равен углу DOC.

Видео:Вписанные и центральные углы #огэ #огэматематика #математикаСкачать

Как найти вписанный угол

Может показаться, что угол, вписанный в окружность, равен центральному углу, который опирается на ту же дугу. Однако это грубая ошибка. На самом деле, даже просто посмотрев на чертеж и сравнив эти углы между собой, можно увидеть, что их градусные меры будут иметь разные значения. Так чему же равен вписанный в окружность угол?

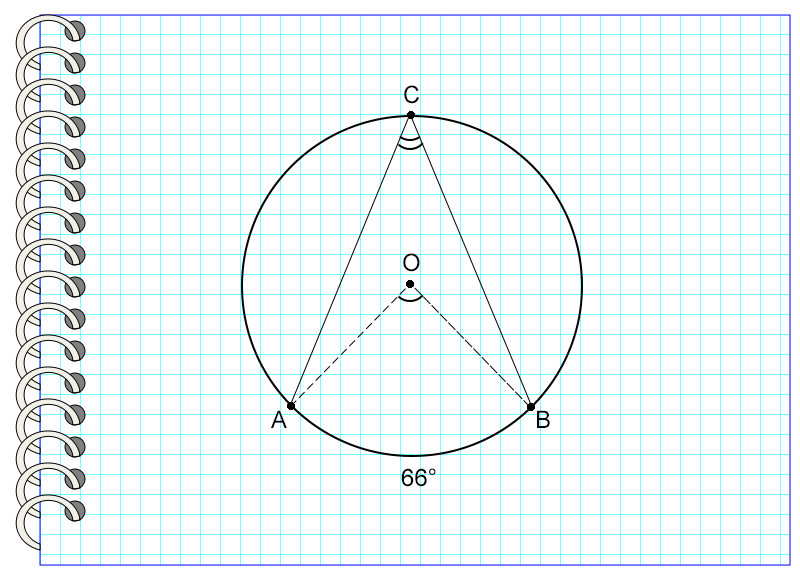
Градусная мера вписанного угла равна одной второй от дуги, на которую он опирается, или половине центрального угла, если они опираются на одну дугу.

Рассмотрим пример. Угол АСВ опирается на дугу, равную 66°.

Значит, угол АСВ = 66° : 2 = 33°

Рассмотрим некоторые следствия из этой теоремы.

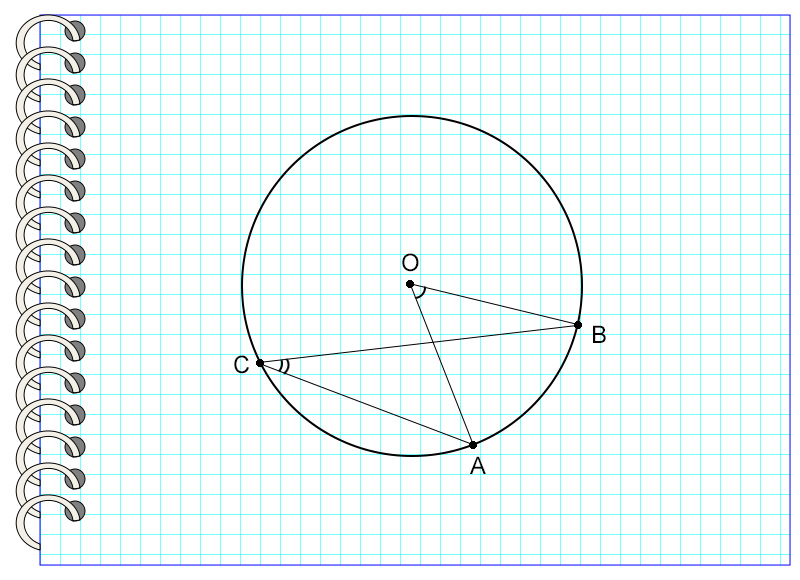
• Вписанные углы, если они опираются на одну и ту же дугу, хорду или равные дуги, равны.
• Если вписанные углы опираются на одну хорду, но их вершины лежат по разные стороны от нее, сумма градусных мер таких углов составляет 180°, так как в этом случае оба угла опираются на дуги, градусная мера которых в сумме составляет 360° (вся окружность), 360° : 2 = 180°
• Если вписанный угол опирается на диаметр данной окружности, его градусная мера равна 90°, так как диаметр стягивает дугу равную 180°, 180° : 2 = 90°
• Если центральный и вписанный углы в окружности опираются на одну дугу или хорду, то вписанный угол равен половине центрального.

Видео:2166 Найдите вписанный угол опирающийся на дугу которая составляет 20 окружностиСкачать

Где могут встретиться задачи на эту тему? Их виды и способы решения

Так как окружность и ее свойства – это один из важнейших разделов геометрии, планиметрии в частности, то вписанный и центральный углы в окружности – это тема, которая широко и подробно изучается в школьном курсе. Задачи, посвященные их свойствам, встречаются в основном государственном экзамене (ОГЭ) и едином государственном экзамене (ЕГЭ). Как правило, для решения этих задач следует найти углы на окружности в градусах.

Видео:Всё про вписанные и центральные углы за 4 минуты | Борис Трушин |Скачать

Углы, опирающиеся на одну дугу

Этот тип задач является, пожалуй, одним из самых легких, так как для его решения нужно знать всего два простых свойства: если оба угла являются вписанными и опираются на одну хорду, они равны, если один из них – центральный, то соответствующий вписанный угол равен его половине. Однако при их решении нужно быть крайне внимательным: иногда бывает сложно заметить это свойство, и ученики при решении таких простейших задач заходят в тупик. Рассмотрим пример.

Дана окружность с центром в точке О. Угол АОВ равен 54°. Найти градусную меру угла АСВ.

Эта задача решается в одно действие. Единственное, что нужно для того, чтобы найти ответ на нее быстро – заметить, что дуга, на которую опираются оба угла — общая. Увидев это, можно применять уже знакомое свойство. Угол АСВ равен половине угла АОВ. Значит,

1) АОВ = 54° : 2 = 27°.

Видео:Задача 6 №27859 ЕГЭ по математике. Урок 104Скачать

Углы, опирающиеся на разные дуги одной окружности

Иногда в условиях задачи напрямую не прописана величина дуги, на которую опирается искомый угол. Для того чтобы ее вычислить, нужно проанализировать величину данных углов и сопоставить их с известными свойствами окружности.

В окружности с центром в точке О угол АОС равен 120°, а угол АОВ – 30°. Найдите угол ВАС.

Для начала стоит сказать, что возможно решение этой задачи с помощью свойств равнобедренных треугольников, однако для этого потребуется выполнить большее количество математических действий. Поэтому здесь будет приведен разбор решения с помощью свойств центральных и вписанных углов в окружности.

Итак, угол АОС опирается на дугу АС и является центральным, значит, дуга АС равна углу АОС.

Точно так же угол АОВ опирается на дугу АВ.

Зная это и градусную меру всей окружности (360°), можно с легкостью найти величину дуги ВС.

ВС = 360° — АС — АВ

ВС = 360° — 120° — 30° = 210°

Вершина угла САВ, точка А, лежит на окружности. Значит, угол САВ является вписанным и равен половине дуги СВ.

Угол САВ = 210° : 2 = 110°

Видео:ЦЕНТРАЛЬНЫЙ угол ВПИСАННЫЙ угол окружности 8 класс АтанасянСкачать

Задачи, основанные на соотношении дуг

Некоторые задачи вообще не содержат данных о величинах углов, поэтому их нужно искать, исходя только из известных теорем и свойств окружности.

Найдите угол, вписанный в окружность, который опирается на хорду, равную радиусу данной окружности.

Если мысленно провести линии, соединяющие концы отрезка с центром окружности, то получится треугольник. Рассмотрев его, можно заметить, что эти линии являются радиусами окружности, а значит, все стороны треугольника равны. Известно, что все углы равностороннего треугольника равны 60°. Значит, дуга АВ, содержащая вершину треугольника, равна 60°. Отсюда найдем дугу АВ, на которую опирается искомый угол.

АВ = 360° — 60° = 300°

Угол АВС = 300° : 2 = 150°

В окружности с центром в точке О дуги соотносятся как 3:7. Найдите меньший вписанный угол.

Для решения обозначим одну часть за Х, тогда одна дуга равна 3Х, а вторая соответственно 7Х. Зная, что градусная мера окружности равна 360°, составим уравнение.

По условию, нужно найти меньший угол. Очевидно, что если величина угла прямо пропорциональна дуге, на которую он опирается, то искомый (меньший) угол соответствует дуге, равной 3Х.

Значит, меньший угол равен (36° * 3) : 2 = 108° : 2 = 54°

В окружности с центром в точке О угол АОВ равен 60°, а длина меньшей дуги — 50. Вычислите длину большей дуги.

Для того чтобы вычислить длину большей дуги, нужно составить пропорцию — как меньшая дуга относится к большей. Для этого вычислим величину обеих дуг в градусах. Меньшая дуга равна углу, который на нее опирается. Ее градусная мера составит 60°. Большая дуга равна разности градусной меры окружности (она равна 360° вне зависимости от остальных данных) и меньшей дуги.

Большая дуга равна 360° — 60° = 300°.

Так как 300° : 60° = 5, то большая дуга в 5 раз больше меньшей.

Большая дуга = 50 * 5 = 250

Итак, конечно, существуют и другие подходы к решению подобных задач, но все они так или иначе основаны на свойствах центральных и вписанных углов, треугольников и окружности. Для того чтобы успешно их решать, необходимо внимательно изучать чертеж и сопоставлять его с данными задачи, а также уметь применять свои теоретические знания на практике.

Видео:Урок по теме ЦЕНТРАЛЬНЫЕ И ВПИСАННЫЕ УГЛЫ 8 КЛАСССкачать

Дано : вписанный в окружность угол АВС опирается на дугу АС, равную 57 градусов?

Геометрия | 5 — 9 классы

Дано : вписанный в окружность угол АВС опирается на дугу АС, равную 57 градусов.

Найти : величину угла АВС.

Вписаный угол равен половине градусной меры дуги, на которую опирается

угол АВС = 57 / 2 = 28.

5 Град = 28 град 30 мин.

Видео:Решение задач на тему центральные и вписанные углы.Скачать

Найдите величину вписанного угла окружности, если центральный угол, опирающийся на ту же дугу, что и вписанный угол, равен 132 градуса?

Найдите величину вписанного угла окружности, если центральный угол, опирающийся на ту же дугу, что и вписанный угол, равен 132 градуса.

Ответ дайте в градусах.

Видео:Вписанный угол, опирающийся на хорду, равную радиусу окружностиСкачать

Найти дугу АС, если р / б треугольник АВС вписан в окружность?

Найти дугу АС, если р / б треугольник АВС вписан в окружность.

АС — основание, &lt ; А = 27 градусам.

Видео:УГОЛ И ОКРУЖНОСТЬ: центральный угол, вписанный угол, длина дуги окружностиСкачать

Вписанный в окружность угол равен 60 градусов?

Вписанный в окружность угол равен 60 градусов.

Вычислите величину вписанного угла опирающегося на ту же дугу.

Видео:Вписанный угол, общий случай.Скачать

В угол АВС вписана окружность?

В угол АВС вписана окружность.

Точки касания делят окружность на дуги, градусные величины которых относятся как 5 : 4.

Найдите величину угла АВС.

Видео:8 класс, 34 урок, Теорема о вписанном углеСкачать

Найти угол CDB, если вписанные углы ADB и ADC опираются на дуги окружности, градусные величины которых равны соответственно 67 градусов и 25 градусов?

Найти угол CDB, если вписанные углы ADB и ADC опираются на дуги окружности, градусные величины которых равны соответственно 67 градусов и 25 градусов.

Видео:№653. Найдите вписанный угол ABC, если дуга АС, на которую он опирается, равна: а) 48°; б) 57°Скачать

Углы АDC и АВС вписаны в окружность?

Углы АDC и АВС вписаны в окружность.

Какой может быть величина угла ADC, если известно, сто угол АВС = 56 градусов.

Видео:72. Градусная мера дуги окружностиСкачать

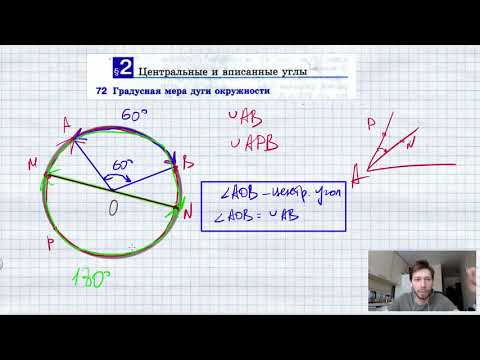
Вписанный угол АВС равен 70 градусов?

Вписанный угол АВС равен 70 градусов.

Чему равен центральный угол, опирающийся на дугу АС ?

Видео:ЕГЭ. Тригонометрический кругСкачать

Равнобедренный треугольник АВС с углом А, равным 30 градусов, вписан в окружность?

Равнобедренный треугольник АВС с углом А, равным 30 градусов, вписан в окружность.

Найти градусную меру меньшей из дуг АС?

Видео:Найти центральный угол (bezbotvy)Скачать

Найти вписаный угол АВС если дуга АС на каторгу он опирается равна 74°?

Найти вписаный угол АВС если дуга АС на каторгу он опирается равна 74°.

Видео:Радианная Мера Угла - Как Переводить Градусы в Радианы // Урок Алгебры 10 классСкачать

Найдите величину вписанного угла окружности, если центральный угол, опирающийся на ту же дугу, что и вписанный угол, равен 132 градуса?

Найдите величину вписанного угла окружности, если центральный угол, опирающийся на ту же дугу, что и вписанный угол, равен 132 градуса.

Ответ дайте в градусах.

Вопрос Дано : вписанный в окружность угол АВС опирается на дугу АС, равную 57 градусов?, расположенный на этой странице сайта, относится к категории Геометрия и соответствует программе для 5 — 9 классов. Если ответ не удовлетворяет в полной мере, найдите с помощью автоматического поиска похожие вопросы, из этой же категории, или сформулируйте вопрос по-своему. Для этого ключевые фразы введите в строку поиска, нажав на кнопку, расположенную вверху страницы. Воспользуйтесь также подсказками посетителей, оставившими комментарии под вопросом.