Видео:8 класс, 32 урок, Касательная к окружностиСкачать

Источник задания: Решение 3055. ОГЭ 2018 Математика, И.В. Ященко. 36 вариантов.
Задание 20. Какое из следующих утверждений верно?
1) Боковые стороны любой трапеции равны.
2) Через любую точку, лежащую вне окружности, можно провести две касательные к этой окружности.
3) Площадь квадрата равна произведению его диагоналей.
В ответ запишите номер выбранного утверждения.
1) Не верно, боковые стороны у трапеции могут различаться по длине.
2) Верно. Из внешней точки окружности можно провести только две касательные к этой окружности.
3) Не верно. Площадь квадрата равна половине произведения его диагоналей.
Видео:Пойми Этот Урок Геометрии и получай 5-ки — Касательная и ОкружностьСкачать

Боковые стороны любой трапеции равны касательная к окружности
Какие из следующих утверждений верны?
1) Существуют три прямые, которые проходят через одну точку.
2) Боковые стороны любой трапеции равны.
3) Сумма углов равнобедренного треугольника равна 180 градусам.
Если утверждений несколько, запишите их номера в порядке возрастания.
Проверим каждое из утверждений.
1) «Существуют три прямые, которые проходят через одну точку» — верно, так как через одну точку на плоскости можно провести бесконечное количество прямых.
2) «Боковые стороны любой трапеции равны» — неверно, боковые стороны равнобедренной трапеции равны.
3) «Сумма углов равнобедренного треугольника равна 180 градусам» — верно, сумма углов любого треугольника равна 180 градусам.
Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Трапеция. Свойства трапеции
Трапеция – четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна).
Параллельные стороны трапеции называются основаниями. Другие две — боковые стороны .
Если боковые стороны равны, трапеция называется равнобедренной .
Трапеция, у которой есть прямые углы при боковой стороне, называется прямоугольной .
Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции .
Видео:№793. Боковые стороны трапеции равны 13 см и 15 см, а периметр равен 48 см. Найдите среднюю линиюСкачать
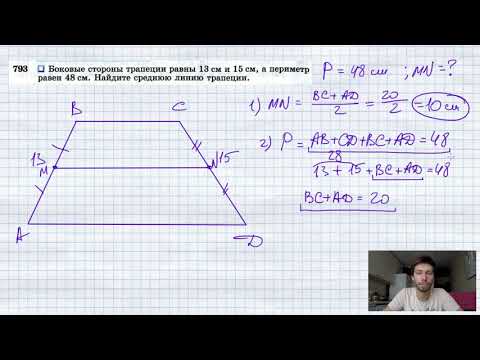
Свойства трапеции
1. Средняя линия трапеции параллельна основаниям и равна их полусумме.
2. Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне.
3. Треугольники и
, образованные отрезками диагоналей и основаниями трапеции, подобны.
Коэффициент подобия –
Отношение площадей этих треугольников есть .
4. Треугольники и
, образованные отрезками диагоналей и боковыми сторонами трапеции, имеют одинаковую площадь.
5. В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон.
6. Отрезок, соединяющий середины диагоналей, равен полуразности оснований и лежит на средней линии.
7. Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.
8. Если сумма углов при любом основании трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности.
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Свойства и признаки равнобедренной трапеции
1. В равнобедренной трапеции углы при любом основании равны.
2. В равнобедренной трапеции длины диагоналей равны.
3. Если трапецию можно вписать в окружность, то трапеция – равнобедренная.
4. Около равнобедренной трапеции можно описать окружность.
5. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.
Видео:Секретная теорема из учебника геометрииСкачать

Вписанная окружность
Если в трапецию вписана окружность с радиусом и она делит боковую сторону точкой касания на два отрезка —
и
, то
Видео:Урок по теме КАСАТЕЛЬНАЯ К ОКРУЖНОСТИСкачать

Площадь
или
где
– средняя линия
Смотрите хорошую подборку задач с трапецией (входят в ГИА и часть В ЕГЭ) здесь и здесь.
Чтобы не потерять страничку, вы можете сохранить ее у себя:
📸 Видео
Задача 6 №27934 ЕГЭ по математике. Урок 148Скачать

Задание 26 Свойство касательной и секущей Подобные треугольникиСкачать

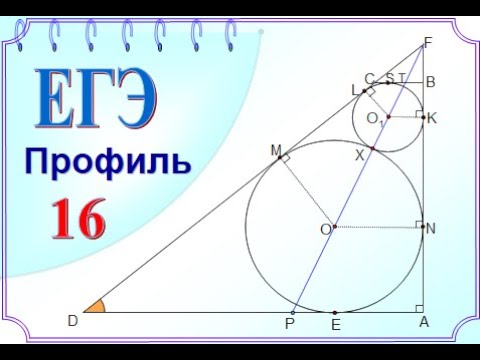
ЕГЭ Задание 16 Две касающиеся окружностиСкачать
ЕГЭ математика 2023 Вариант 2 задача 1Скачать
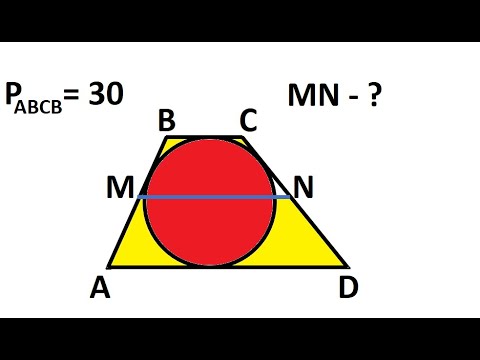
Угол между хордой и касательнойСкачать

Боковые стороны трапеции, описанной около окружности, равны 13 и 1. Найдите среднюю линию трапеции.Скачать
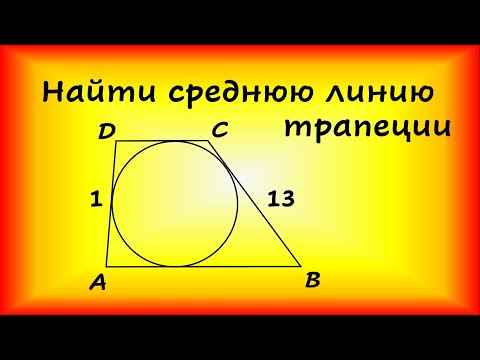
#159 ТРАПЕЦИЯ И КРУГ // СУММА УГЛОВСкачать

Геометрия 5. Касательная к окружности.Скачать

Касательные к окружности | Задачи 11-20 | Решение задач | Волчкевич | Уроки геометрии 7-8 классСкачать

Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Отрезки касательных из одной точки до точек касания окружности равны | Окружность | ГеометрияСкачать

Касательная к окружности и её свойстваСкачать

Геометрия 11-3. Трапеции, вписанные в окружность и описанные около окружности. Задача 3Скачать


















