Итак, с сегодняшнего дня мы начинаем вести новую рубрику: «Решение задач», в которой будем рассматривать задачи, взятые из сборника М.Э.Абрамяна «1000 ЗАДАЧ ПО ПРОГРАММИРОВАНИЮ».
Открыв задачник и прочитав аннотацию, Вы, скорее всего, озадачитесь тем, что данное пособие предназначено для студентов механико-математического, физического и экономического факультетов, но смею Вас заверить, что это весьма универсальная книга, которая подходит как студентам, так и школьникам. Возможно, задачи из первых разделов книги покажутся Вам простыми — в этом случае используйте наш разбор только для проверки своих решений; но если же по каким-либо причинам решить задачи Вы не в состоянии, то тогда присоединяйтесь к нам.
Begin1. Дана сторона квадрата a. Найти его периметр P = 4·a.
Прежде всего напомню, что для ввода и вывода информации, в Паскале используют следующие операторы:
- Read (Readln) — ввод значений с клавиатуры;
- Write (Writeln) — вывод результата (и вообще чего-либо) на экран.
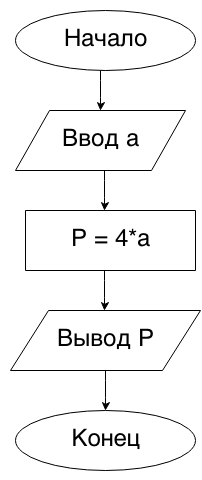
Таким образом, решение задачи становится очевидным.
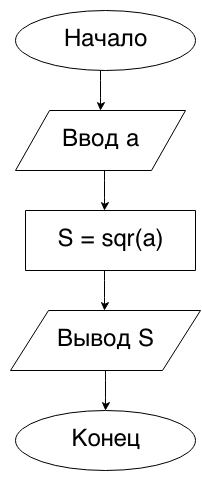
Begin2. Дана сторона квадрата a. Найти его площадь S = a 2 .
При решении данной задачи воспользуемся функцией sqr . Можно, конечно, вычислять квадрат, умножая число само на себя (S=a*a), но при вводе действительно больших чисел наша программа будет выполняться гораздо дольше, нежели при использовании sqr .
Begin3°. Даны стороны прямоугольника a и b. Найти его площадь S = a·b и периметр P = 2·(a + b).
Да, задача по сути своей проста и подобна предыдущим, поэтому поскорее составим к ней решение и перейдем к следующей.

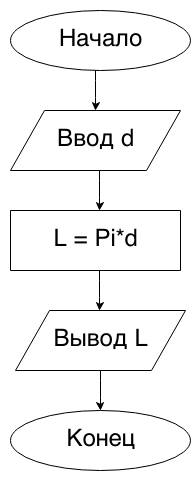
Begin4. Дан диаметр окружности d. Найти ее длину L = π·d. В качестве значения π использовать 3.14.
У вас, наверняка, возникает вопрос π — это константа или переменая? Так как π не изменяется в течение программы, π — константа. Вообще в Паскале уже встроена такая константа, но ее значение:
А так как в условии задачи указано, что в качестве значения π нужно использовать 3.14, то следует объявить π в разделе описания констант.
Begin5. Дана длина ребра куба a. Найти объем куба V = a 3 и площадь его поверхности S = 6·a 2 .
Для решения задачи используем функцию power(x, a), где a — степень, x — число возводимое в степень (разумеется, использовать ее мы будем только для возведения числа в третью степень, квадрат числа по-прежнему находим с помощью sqr(x) ).

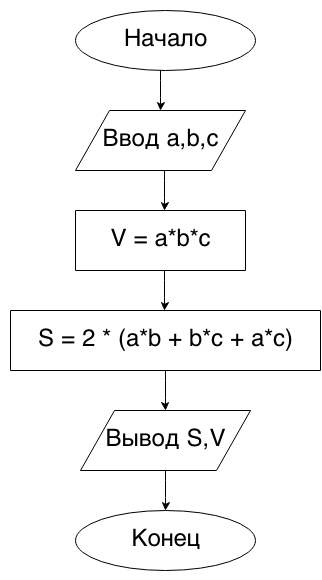
Begin6. Даны длины ребер a, b, c прямоугольного параллелепипеда. Найти его объем V = a·b·c и площадь поверхности S = 2·(a·b + b·c + a·c).
Begin7°. Найти длину окружности L и площадь круга S заданного радиуса R:
L = 2·π·R, S = π·R 2 .
В качестве значения π использовать 3.14.

Begin8. Даны два числа a и b. Найти их среднее арифметическое: (a + b)/2.
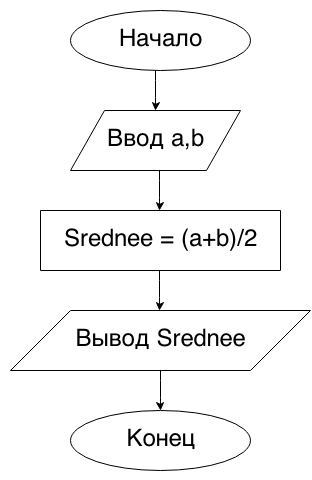
Begin9. Даны два неотрицательных числа a и b. Найти их среднее геометрическое, то есть квадратный корень из их произведения: √(a*b).
Напомню, что для нахождения квадратного корня мы используем функцию sqrt .
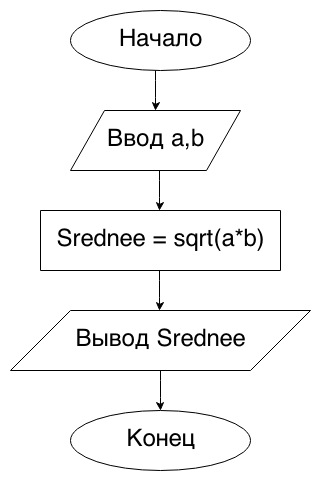
Begin10. Даны два ненулевых числа. Найти сумму, разность, произведение и частное их квадратов.
Ну вот и все. Следующая публикация с решением задач выйдет в ближайшие дни.
- Содержание
- Лекция 1. Понятие алгоритма. Виды алгоритмов
- Краткие итоги
- Вопросы
- Упражнения
- Лекция 2. Блок-схемы. Графическая реализация алгоритмов
- Занятие 1. Понятие блок-схемы. Основные виды блоков
- Занятие 2. Графическая реализация линейного алгоритма
- Занятие 3. Графическая реализация разветвляющегося алгоритма
- Занятие 4. Графическая реализация циклического алгоритма
- Занятие 5. Выполнение блок-схем
- Определение принадлежности точки кругу с центром в начале координат
- Pascal
- Язык Си
- Python
- 🌟 Видео
Видео:Блок-схемы для начинающих (Блок схемы алгоритмов)Скачать

Содержание
Видео:Самый подробный урок про Блок-схемы, Понимание, Чтение и Создание блок-схемСкачать

Лекция 1. Понятие алгоритма. Виды алгоритмов
Алгоритм является базовым понятием для тех, кто хочет начать программировать на любом языке программирования. Любая задача может быть формализована алгоритмически. Чтобы понять, с чего начать, рассмотрим основные виды алгоритмов.
Цель данной лекции – ознакомить студентов с понятием алгоритма; показать, что такая абстрактная вещь как алгоритм окружает нас в повседневной жизни.
Существует несколько определений понятия алгоритма. Приведем два самых распространенных.
Алгоритм – последовательность чётко определенных действий, выполнение которых ведёт к решению задачи. Алгоритм, записанный на языке машины, есть программа решения задачи.
Алгоритм – это совокупность действий, приводящих к достижению результата за конечное число шагов.
Вообще говоря, первое определение не передает полноты смысла понятия алгоритм. Используемое слово «последовательность» сужает данное понятие, т.к. действия не обязательно должны следовать друг за другом – они могут повторяться или содержать условие.
- Дискретность (от лат. discretus — разделенный, прерывистый) – это разбиение алгоритма на ряд отдельных законченных действий (шагов).
- Детерминированность (от лат. determinate — определенность, точность) — любое действие алгоритма должно быть строго и недвусмысленно определено в каждом случае. Например, алгоритм проезда к другу, если к остановке подходят автобусы разных маршрутов, то в алгоритме должен быть указан конкретный номер маршрута 5. Кроме того, необходимо указать точное количество остановок, которое надо проехать, скажем, три.
- Конечность – каждое действие в отдельности и алгоритм в целом должны иметь возможность завершения.
- Массовость – один и тот же алгоритм можно использовать с разными исходными данными.
- Результативность – алгоритм должен приводить к достоверному решению.
Основная цель алгоритмизации – составление алгоритмов для ЭВМ с дальнейшим решением задачи на ЭВМ.
- Любой прибор, купленный в магазине, снабжается инструкцией по его использованию. Данная инструкция и является алгоритмом для правильной эксплуатации прибора.
- Каждый шофер должен знать правила дорожного движения. Правила дорожного движения однозначно регламентируют поведение каждого участника движения. Зная эти правила, шофер должен действовать по определенному алгоритму.
- Массовый выпуск автомобилей стал возможен только тогда, когда был придуман порядок сборки машины на конвейере. Определенный порядок сборки автомобилей – это набор действий, в результате которых получается автомобиль.
Существует несколько способов записи алгоритмов. На практике наиболее распространены следующие формы представления алгоритмов:
- словесная (запись на естественном языке);
- псевдокоды (полуформализованные описания алгоритмов на условном алгоритмическом языке, включающие в себя как элементы языка программирования, так и фразы естественного языка, общепринятые математические обозначения и др.);
- графическая (изображения из графических символов – блок-схема);
- программная (тексты на языках программирования – код программы).
Рассмотрим подробно каждый вариант записи алгоритамов на примере следующей задачи. Требуется найти частное двух чисел.
Словесный способ записи алгоритмов представляет собой описание последовательных этапов обработки данных. Алгоритм задается в произвольном изложении на естественном языке. Ответ при этом получает человек, который выполняет команды согласно словесной записи.
Пример словесной записи:
- задать два числа, являющиеся делимым и делителем;
- проверить, равняется ли делитель нулю;
- если делитель не равен нулю, то найти частное, записать его в ответ;
- если делитель равен нулю, то в ответ записать «нет решения».
Словесный способ не имеет широкого распространения, так как такие описания: строго не формализуемы; страдают многословностью записей; допускают неоднозначность толкования отдельных предписаний.
Псевдокод занимает промежуточное место между естественным и формальным языками. С одной стороны, он близок к обычному естественному языку, поэтому алгоритмы могут на нем записываться и читаться как обычный текст. С другой стороны, в псевдокоде используются некоторые формальные конструкции и математическая символика, что приближает запись алгоритма к общепринятой математической записи. В псевдокоде не приняты строгие синтаксические правила для записи команд, присущие формальным языкам, что облегчает запись алгоритма на стадии его проектирования и дает возможность использовать более широкий набор команд, рассчитанный на абстрактного исполнителя. Однако в псевдокоде обычно имеются некоторые конструкции, присущие формальным языкам, что облегчает переход от записи на псевдокоде к записи алгоритма на формальном языке. Ответ при этом получает человек, который выполняет команды согласно псевдокоду.
Приведем основные управляющие структуры псевдокода в табл. 1.1.
| Название структуры | Псевдокод | ||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Присваивание | |||||||||||||||||||||||
| Повторение | В данном примере используется три переменные: делимое, делитель и частное. Делимое и делитель задаются исполнителем произвольными числами. Частное считается лишь в том случае, если делитель не равен нулю. Графическая реализация алгоритма представляет собой блок-схему. Блок-схема состоит из блоков определенной формы, соединенных стрелками. Ответ при этом получает человек, который выполняет команды согласно блок-схеме. Более подробно о блок-схемах будет рассказано в Лекции 2. Программная реализация алгоритма – это компьютерная программа, написанная на каком-либо алгоритмическом языке программирования, например: С++, Pascal, Basic и т.д. Программа состоит из команд определенного языка программирования. Отметим, что одна и та же блок-схема может быть реализована на разных языках программирования. Ответ при этом получает ЭВМ, а не человек. Более подробно о составлении программ на языке программирования С++ смотреть Лекцию 3. Различают три основных вида алгоритмов:
Линейный алгоритм – это алгоритм, в котором действия выполняются однократно и строго последовательно. Самый простой пример реализации линейного алгоритма – путь из университета домой. Словесный способ записи данного алгоритма:
Очевидно, что данный пример относится к линейному алгоритму, т.к. все действия следуют одно за другим, без условий и повторений. Разветвляющийся алгоритм – это алгоритм, в котором в зависимости от условия выполняется либо одна, либо другая последовательность действий. Самый простой пример реализации разветвляющегося алгоритма – если на улице идет дождь, то необходимо взять зонт, иначе не брать зонт с собой. Приведенный выше пример псевдокода по нахождению частного двух чисел также относится к разветвляющемуся алгоритму. Циклический алгоритм – это алгоритм, команды которого повторяются некое количество раз подряд. Самый простой пример реализации циклического алгоритма – при чтении книги будут повторяться одни и те же действия: прочитать страницу, перелистнуть и т.д. Более подробно о линейном, разветвляющемся и циклическом алгоритмах смотреть Лекцию 2. Краткие итогиЛюбая задача может быть разбита на элементарные действия. Для любой математической задачи или ситуации из жизни можно составить алгоритм решения. Алгоритм может быть описан словесно, псевдокодом, графически или программно. Задача всегда решается с помощью базовых типов алгоритма – линейного, разветвляющегося или циклического. Вопросы
Упражнения
Видео:0.Блок схема. 8 классСкачать  Лекция 2. Блок-схемы. Графическая реализация алгоритмовБлок-схемы представляют собой наглядную реализацию алгоритма. Рассмотрим, как графически представлять разные виды алгоритмов на математических задачах и ситуациях из жизни. Цель данной лекции – ознакомить студентов с понятием блок-схемы; показать основные конструкции реализации разных видов алгоритма; показать принципы проверки блок-схем и получения по ним ответа. Занятие 1. Понятие блок-схемы. Основные виды блоковБлок-схема – это графическая реализация алгоритма. Блок-схема представляет собой удобный и наглядный способ записи алгоритма. Блок-схема состоит из функциональных блоков разной формы, связанных между собой стрелками. В каждом блоке описывается одно или несколько действий. Основные виды блоков представлены в табл. 2.1.
Любая команда алгоритма записывается в блок-схеме в виде графического элемента – блока, и дополняется словесным описанием. Блоки в блок-схемах соединяются линиями потока информации. Направление потока информации указывается стрелкой. В случае потока информации сверху вниз и слева направо стрелку ставить не обязательно. Блоки в блок-схеме имеют только один вход и один выход (за исключением логического блока – блока с условием). Блок начала блок-схемы имеет один выход и не имеет входов, блок конца блок-схемы имеет один вход и не имеет выходов. Блок условия – единственный блок, имеющий два выхода, т.к. соответствует разветвляющемуся алгоритму. На одном выходе указывается «да», на другом – «нет». Все остальные блоки имеют один вход и один выход. Блок выполнения действия может содержать присвоение значения переменной (например » Математические выражения и логические высказывания должны быть описаны математическим языком, т.к. блок-схема не должна иметь привязки к какому-то определенному языку программирования. Одна и таже блок-схема может быть реализована в программах на разных языках программирования. К примеру, функция в блок-схеме будет выглядеть таким образом: Все три вида алгоритмов реализуются в блок-схеме названными выше типами блоков. К примеру, в линейном алгоритме могут присутствовать все блоки, кроме блока условия. В разветвляющемся и циклическом алгоритмах могут быть использованы все названные виды блоков, но обязательным является блок условия. Внутри блока условия записывается условие, про которое можно однозначно ответить, истинно оно или ложно Если условие истинно, то выполняются действия, соответствующие стрелке «да», иначе стрелке «нет». Занятие 2. Графическая реализация линейного алгоритмаПриведем простейшие примеры, соответствующие линейному алгоритму. Пример 1. Вася хочет позвонить Пете по городскому телефону. Необходимо составить блок-схему, описывающую порядок действий Васи. Решение. Чтобы позвонить по городскому телефону, нужно знать номер Пети. Значит, сначала надо найти номер телефона Пети, набрать его и поговорить с Петей. На этом цель Васи (поговорить с Петей по телефону) будет достигнута. Результат блок схемы представлен на рис. 2.1. Пример 2. Ученику требуется купить учебник. Составить блок-схему, описывающую порядок действий ученика. Решение. Сначала ученику нужно взять деньги, потом прийти в книжный магазин и заплатить за учебник. На этом цель (покупка учебника) будет достигнута. Результат блок схемы представлен на рис. 2.2. Пример 3. Даны числа Решение. Сначала следует задать значения для чисел В блок-схеме на рис. 2.3а каждое действие расположено в отдельном блоке. В блок-схеме рис. 2.3б объединены между собой схожие по смыслу операции. В дальнейшем мы будем объединять некоторые действия в один блок. Это очень удобно и визуально упрощает чтение блок-схемы. Занятие 3. Графическая реализация разветвляющегося алгоритмаВ разветвляющемся алгоритме обязательным блоком является блок условия, который представлен на рис. 2.4. Внутри блока условия записывается условие. Если данное условие верно, то выполняются блоки, идущие по стрелке «да», т.е. «Набор действий 1». Если условие оказывается неверным, т.е. ложным, то выполняются блоки, идущие по стрелке «нет», а именно «Набор действий 2». Разветвление заканчивается, когда обе стрелки («да» и «нет») соединяются. На рис. 2.5 представлен еще один вариант использования блока условия. Бывают задачи, в которых, исходя из условия, необходимо либо выполнить действие, либо пропустить его. Если условие верно выполняется, то следуют блоки, соответствующие стрелке «да», т.е. «Набор действий 1». Если же условие оказывается ложным, то следует перейти по стрелке «нет». Т.к. стрелке «нет» не соответствует ни одного блока с действием, то ни одного действия не будет выполнено. Т.е. получается, что мы пропустили и не выполнили «Набор действий 1». В разветвляющемся алгоритме возможна запись сразу нескольких условий, которые могут объединяться союзом «ИЛИ» или пересекаться союзом «И». Рассмотрим случай двух условий: «условие 1» и «условие 2». Если необходимо, чтобы оба условия были верными одновременно, то следует использовать логическое пересечение «И»: Если достаточно, чтобы только одно условие выполнялось – либо первое, либо второе, то следует использовать логическое объединение «ИЛИ»: Приведем простейшие примеры, соответствующие разветвляющемуся алгоритму. Пример 4. Джон звонит Полу по городскому телефону, но трубку может взять не только Пол. Составить блок-схему, описывающую действия Джона в этом случае. Решение. В отличие от примера 1, здесь присутствует условие – Пол ли взял трубку телефона. На данное условие можно однозначно ответить: «да», Пол, или «нет», кто-то другой. Если трубку взял Пол, то Джону нужно с ним поговорить, и цель будет достигнута. Если трубку взял кто-то другой, то необходимо позвать Пола к телефону, поговорить с ним, и цель также будет достигнута. Третьего варианта, например, «не туда попали» или «его нет дома» мы не рассматриваем. Результат блок-схемы представлен на рис. 2.6. Пример 5. Ученику требуется купить учебник. В магазине в наличие оказался нужный учебник в жесткой и мягкой обложке. Составить блок-схему, описывающую действия ученика. Решение. В данном примере присутствует условие: «Нужна жесткая обложка». Ученик может согласиться с этим высказыванием, тогда он выполнит действие, соответствующее стрелке «да» и купит учебник в жесткой обложке. Если ученик не соглашается с данным условием, то будет выполняться действие, соответствующее стрелке «нет», и в этом случае ученик купит учебник в мягкой обложке. И в том, и в другом случае, цель будет достигнута и задача будет выполнена, т.к. ученик купит учебник. Результат блок схемы представлен на рис. 2.7. Пример 6. Даны числа Решение. Как и в примере 3, сначала необходимо задать значения Занятие 4. Графическая реализация циклического алгоритмаВ рассмотрении циклического алгоритма следует выделить несколько понятий. Тело цикла – это набор инструкций, предназначенный для многократного выполнения. Итерация – это единичное выполнение тела цикла. Переменная цикла – это величина, изменяющаяся на каждой итерации цикла. Каждый цикл должен содержать следующие необходимые элементы:
Циклы бывают двух видов – с предусловием и с постусловием. В цикле с предусловием сначала проверяется условие входа в цикл, а затем выполняется тело цикла, если условие верно. Цикл с предусловием представлен на рис. 2.9. Цикл с предусловием также может быть задан с помощью счетчика. Это удобно в тех случаях, когда точно известно количество итераций. В общем виде блок-схема, реализующая цикл с предусловием, представлена ниже. Сначала задается начальное значение переменной цикла, затем условие входа в цикл, тело цикла и изменение переменной цикла. Выход из цикла осуществляется в момент проверки условия входа в цикл, когда оно не выполняется, т.е. условие ложно. Цикл с предусловием может ни разу не выполниться, если при первой проверке условия входа в цикл оно оказывается ложным. В цикле с постусловием сначала выполняется тело цикла, а потом проверяется условие. Циклический алгоритм с постусловием представлен на рис. 2.10. Если условие верно, то итерация повторяется, если же неверно, то осуществляется выход из цикла. В отличие от цикла с предусловием, любой цикл с постусловием всегда выполнится хоть раз. Примечание. Как видно из представленных блок-схем для циклов с предусловием и постусловием, условие записывается внутри блока условия (формы ромба), как и в разветвляющемся алгоритме. Принципиальная разница между разветвляющимся и циклическим алгоритмами при графической реализации состоит в том, что в циклическом алгоритме в обязательном порядке присутствует стрелка, идущая наверх. Именно эта стрелка обеспечивает многократный повтор тела цикла. Приведем простейшие примеры, соответствующие циклическому алгоритму. Пример 7. Вася звонит Пете, но у Пети может быть занята линия. Составить блок-схему действий Васи в этом случае. Решение. Когда телефонная линия занята, то необходимо снова и снова набирать номер, пока Петя не закончит предыдущий разговор, и телефонная линия не окажется вновь свободной. Блок-схема представлена на рис. 2.11. Здесь тело цикла состоит из одного действия «Набрать номер Пети», т.к. именно это действие следует повторять, пока линия будет занята. Под итерацией цикла понимается очередная попытка дозвониться до Пети. Как таковой переменной цикла здесь нет, т.к. ситуация взята из жизни. Выход из цикла происходит в тот момент, когда условие «У Пети занято» стало неверным, т.е. телефонная линия свободна – действительно, нет необходимости больше набирать номер Пети. В данном примере применен цикл с постусловием, т.к. сначала необходимо набрать номер Пети, ведь иначе мы не можем ответить на вопрос – занята ли линия у Пети. Пример 8. Ученику требуется купить учебник. Составить блок-схему, описывающую действия ученика в случае, если учебника нет в ряде магазинов. Решение. Действия ученика в данном примере очевидны: когда он приходит в первый и любой последующий магазины, то возможны два варианта – учебник имеется в наличии или учебника нет в продаже. Если учебника нет в продаже, то ученику следует пойти в другой книжный магазин и спросить данный учебник, и т.д. пока учебник не будет куплен, т.к. перед учеником стоит конечная цель – купить учебник. Мы будем использовать цикл с предусловием, т.к. сначала требуется найти магазин, имеющий в наличии данный учебник. Цикл будет выполняться, пока условие «В данном магазине нет учебника» будет верным, а выход из цикла осуществится, когда условие станет ложным, т.е. когда ученик придет в магазин, в котором есть данный учебник. Действительно, в этом случае ученик купит нужный ему учебник и не будет больше искать книжные магазины. Результат блок-схемы представлен на рис. 2.12. Здесь тело цикла состоит из одного действия «Найти другой книжный магазин». Переменной цикла в явном виде нет, но можно подразумевать номер магазина, в который пришел ученик в очередной раз. Как любой другой цикл с предусловием, данный цикл может ни разу не выполниться (не иметь итераций), если в первом же магазине окажется нужный учебник. Примечание. Если в данную задачу добавить условие выбора учебника в жесткой или мягкой обложке, как в примере 5, то оно появится после выхода из цикла. На реализацию циклического алгоритма данное условие не повлияет. Пример 9. Даны числа Решение. В отличие от примеров 3 и 6 здесь число Тело цикла состоит из нескольких действий: вычисление суммы, вычисление разности и вывод полученных данных на экран. Таким образом, у нас получится несколько значений сумм и разностей, т.к. Данная задача может быть сделана и с циклом с предусловием, и с постусловием. В этом случае тело цикла, условие и изменение переменной цикла будут такими же, как и в цикле с предусловием, но сначала необходимо выполнить тело цикла, а потом проверить условие для выполнения следующей итерации. Приведем блок-схему, использующую цикл с постусловием, на рис. 2.14. В данной задаче также могут быть соединены циклический и разветвляющийся алгоритмы, если по условию задачи требуется сравнить полученные значения суммы и разности, как в примере 6. В этом случае цикл можно реализовать как с предусловием, так и с постусловием, а сравнение суммы и разности добавится внутрь тела цикла, т.к. следует сравнить между собой все полученные суммы и разности. Организация самого цикла останется прежней. Приведем на рис. 2.15а блок-схему с предусловием, а на рис. 2.15б блок-схему с постусловием. Занятие 5. Выполнение блок-схемБлок-схема сама по себе не содержит ответа. Чтобы получить результат, нужно выполнить блок-схему. Выполнение блок-схемы – это прохождение всех действий блок-схемы согласно алгоритму от блока Начало до блока Конец для получения результата. Если блок-схема составлена корректно, то, выполнив ее, человек получит ответ к своей задаче. Если же при составлении блок-схемы были допущены ошибки, то исполнитель либо вообще не дойдет до блока Конец, либо получит неверный ответ. Для выполнения нам понадобится поле для расчетов (аналог «оперативной памяти») и поле для вывода результата (аналог экрана для вывода данных). Экран будем показывать несколько раз в зависимости от вывода новых данных на экране. Выполнение блок-схемы для примера 3. Даны числа Выполнение блок-схемы приведем в табл. 2.2.
|






 «) или вычисление (например »
«) или вычисление (например »  «).
«). , а не таким образом:
, а не таким образом:  .
.

 . Вычислить сумму
. Вычислить сумму  и разность
и разность  чисел
чисел  и
и  .
. . Полученные значения суммы и разности нужно будет показать на экране, и мы используем блок вывода данных. Если не выводить данные на экран, то пользователь нашего алгоритма не узнает, какие получились значения суммы и разности. Результат блок схемы представлен на рис. 2.3.
. Полученные значения суммы и разности нужно будет показать на экране, и мы используем блок вывода данных. Если не выводить данные на экран, то пользователь нашего алгоритма не узнает, какие получились значения суммы и разности. Результат блок схемы представлен на рис. 2.3.




 . Если полученная сумма
. Если полученная сумма  «. Если же условие окажется ложным (т.е.
«. Если же условие окажется ложным (т.е.  ), то пойдем по стрелке «нет» и выведем фразу »
), то пойдем по стрелке «нет» и выведем фразу »  «. Результат блок схемы представлен на рис. 2.8.
«. Результат блок схемы представлен на рис. 2.8.




 . Известно, что число
. Известно, что число  меняется от -10 до 10 с шагом 5,
меняется от -10 до 10 с шагом 5,  и не изменяется. Вычислить сумму
и не изменяется. Вычислить сумму  «. Итак,
«. Итак, 




![Основы программирования. Алгоритмы и блок-схемы. Урок 6 [GeekBrains]](https://i.ytimg.com/vi/sDwDhDJFbOw/0.jpg)





![Как строить блок-схемы и рисовать бизнес-процессы [для начинающих]](https://i.ytimg.com/vi/p5-MDUBNWLE/0.jpg)








