Во всех школах в старших классах проходят курс стереометрии, в котором рассматривают характеристики различных пространственных фигур. Данная статья посвящена изучению свойств одной из таких фигур. Рассмотрим, что такое правильная треугольная призма.
- Призма в геометрии
- Правильная треугольная призма
- Площадь поверхности
- Формула для определения объема фигуры
- Решение задачи
- Правильная треугольная призма
- Треугольная призма — это многогранник,две грани которого являются равными треугольниками, лежащими в параллельных плоскостях, а остальные грани (боковые грани) — параллелограммами, имеющими общие стороны с этими треугольниками.
- Правильная треугольная призма — это треугольная призма у которой основания правильные треугольники (все стороны которых равны, углы между сторонами основания составляют 60 градусов), а боковые грани прямоугольники.
- Правильная треугольная призма: определение, формулы для площади поверхности и объема
- Определение
- Треугольная призма
- Площадь поверхности
- Виды фигуры
- Найти объем призмы, зная площадь основания и высоту
- Площадь поверхности и объём
- Решение простого примера
- Элементы правильной четырехугольной призмы
- Как выглядит призма
- Как рассчитывать объем фигуры произвольного типа?
- Задачи на расчет треугольной призмы
- Общая теория
- Призма в геометрии
- Площадь правильной шестиугольной призмы
Видео:№227. Основание призмы — правильный треугольник ABC. Боковое ребро АА1 образует равныеСкачать

Призма в геометрии
Согласно стереометрическому определению, призма является объемной фигурой, состоящей из n параллелограммов и двух одинаковых n-угольных оснований, где n — это целое положительное число. Оба основания расположены в параллельных плоскостях, а параллелограммы соединяют попарно их стороны в единую фигуру.
Любую призму можно получить следующим способом: следует взять плоский n-угольник и переместить его параллельно самому себе в другую плоскость. В процессе перемещения вершины n-угольника прочертят n отрезков, которые будут боковыми ребрами призмы.
Призмы могут быть выпуклыми и вогнутыми, прямыми и косоугольными, правильными и неправильными. Все эти виды фигур отличаются друг от друга формой n-угольников в основании, а также их расположением относительно перпендикулярного им отрезка, длина которого является высотой призмы. Ниже рисунок демонстрирует набор призм с разным числом углов в основании и количеством боковых граней.
Видео:№228. Основанием наклонной призмы АВСА1В1С1 является равнобедренный треугольник ABCСкачать
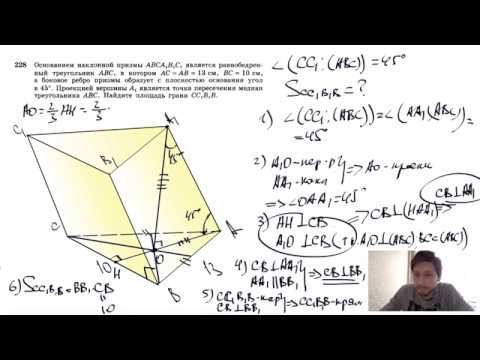
Правильная треугольная призма
Первая призма на фотографии выше является правильной треугольной. Она состоит из двух одинаковых равносторонних треугольников и из трех прямоугольников. Прямоугольник является частным случаем параллелограмма, поэтому рассматриваемая фигура удовлетворяет изложенному ранее стереометрическому определению.
Помимо пяти граней, треугольная призма образована шестью вершинами, которые принадлежат обоим основаниям, и девятью ребрами, три из которых являются боковыми.
Важным свойством правильной треугольной призмы является то, что ее высота совпадает с длиной бокового ребра. Все эти ребра равны друг другу, а боковые прямоугольники пересекают основания под прямыми углами. Отметим, что прямые двугранные углы между основаниями и боковыми гранями приводят к тому, что параллелограммы наклонной призмы становятся прямоугольниками в прямой фигуре. Очевидно, что при определенных длинах ребер прямоугольники могут стать квадратами.
Важными свойствами любой объемной фигуры являются площадь ее поверхности и заключенный в ней объем пространства. Изучаемая призма не является исключением, поэтому рассмотрим ее подробные характеристики.
Видео:№230. Основание прямой призмы — треугольник со сторонами 5 см и 3 см и углом, равным 120Скачать

Площадь поверхности
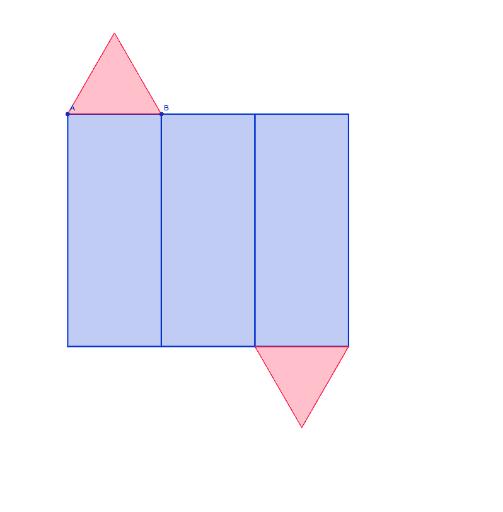
Площадь правильной треугольной призмы образована площадями всех ее пяти граней. Известно, что площадь пространственных фигур проще рассматривать и изучать на плоскости, поэтому удобно сделать развертку призмы. Она показана ниже.
Развертка представлена пятью фигурами двух типов, которые в призме являлись гранями.
Для определения площади всех этих фигур введем следующие обозначения: будем считать длину стороны основания равной a, а высоту (длину бокового ребра) равной h. С учетом обозначений получаем площадь одного треугольника:
При записи этой формулы использовалось стандартное выражение для площади треугольника. Площадь одного прямоугольника равна:
С учетом числа треугольников и прямоугольников (см. развертку выше) получим формулу для площади полной поверхности изучаемой геометрической фигуры:
Здесь первый член в правой части равенства описывает площадь двух оснований, второй член позволяет вычислить площадь поверхности боковой.
Напомним, что полученная для S формула справедлива только для прямой правильной треугольной призмы. Если бы мы рассматривали наклонную фигуру, то выражение для S имело бы другой вид.
Видео:Геометрия Равносторонний треугольникСкачать

Формула для определения объема фигуры
Объемом любой пространственной фигуры называется та часть пространства, которую ограничивают грани многогранника. Объем любой призмы, независимо от формы ее основания и боковых сторон, может быть определен по следующей формуле:
То есть достаточно умножить площадь одного основания на высоту всей фигуры, чтобы получить искомое значение объема.
Для случая треугольной правильной призмы получаем следующее выражение для V:
Записанная формула для V, а также выражение для S в предыдущем пункте зависят всего от двух параметров фигуры: длин a и h. То есть знание всего двух любых линейных параметров позволяет рассчитать все свойства изучаемой призмы.
Видео:№233. Основанием прямой призмы АВСA1B1C1 является прямоугольный треугольник ABCСкачать

Решение задачи
В физике треугольная правильная призма, изготовленная из сплошного стекла, часто применяется для разложения электромагнитного потока в видимой области спектра на ряд частот с целью их изучения. Необходимо определить, какой объем стекла понадобится, чтобы изготовить призму с площадью поверхности 300 см 2 и длиной стороны основания 10 см.
Сначала определим высоту призмы h. Воспользуемся формулой для S, имеем:
h = (S — √3 / 2 × a 2 ) / (3 × a) = (300 — √3 / 2 × 10 2 ) / (3 × 10) = 7,11 см
Поскольку мы знаем значения a и h, то для определения объема призмы воспользуемся формулой для V:
V = √3 / 4 × a 2 × h = √3 / 4 × 10 2 × 7,11 = 307,87 см 3
Таким образом, чтобы изготовить описанную призму, понадобится около 308 см 3 стекла.
Видео:№234. Основанием прямой призмы является прямоугольный треугольник. Через середину гипотенузыСкачать

Правильная треугольная призма
Видео:Равнобедренный треугольник. 7 класс.Скачать

Треугольная призма — это многогранник,две грани которого являются равными треугольниками, лежащими в параллельных плоскостях, а остальные грани (боковые грани) — параллелограммами, имеющими общие стороны с этими треугольниками.
Видео:Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать

Правильная треугольная призма — это треугольная призма у которой основания правильные треугольники (все стороны которых равны, углы между сторонами основания составляют 60 градусов), а боковые грани прямоугольники.
Основания призмы являются равными правильными треугольниками.
Боковые грани призмы являются прямоугольниками.
Боковые рёбра призмы параллельны и равны.
Размеры призмы можно выразить через длину стороны a и высоту h.
Площадь полной поверхности призмы равна сумме площади её боковой поверхности и удвоенной площади основания.
Формула площади поверхности треугольной призмы:
Объём призмы равен произведению её высоты на площадь основания.
Формула объема правильной треугольной призмы:
Правильная треугольная призма может быть вписана в цилиндр.
Формула радиуса цилиндра вписанной треугольной призмы:
Исторически понятие «призма» возникло из латыни и означало — нечто отпиленное.
Анимация демонстрирует как две параллельные плоскости отрезая лишнее формируют два основания призмы. Из одной заготовки можно получить как правильную призму, так и наклонную призму.
Видео:№235. Основанием прямой призмы является прямоугольный треугольник с острым углом φ. ЧерезСкачать
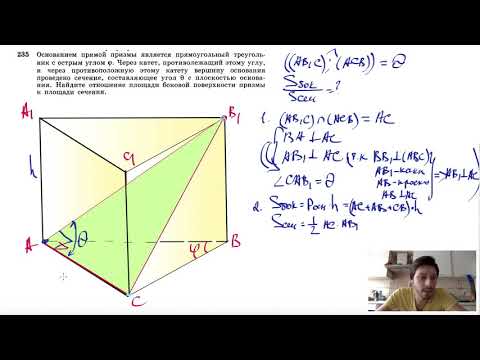
Правильная треугольная призма: определение, формулы для площади поверхности и объема
Видео:Геометрия 7 класс (Урок№13 - Равнобедренный треугольник.)Скачать

Определение
Треугольная призма — это пятигранник, образованный двумя параллельными плоскостями, в которых расположены два треугольника, образующих две грани призмы, и оставшиеся три грани — параллелограммы, образованные со-сторонами треугольников.
Видео:Как построить равнобедренный или равносторонний треугольник по клеткам.Скачать

Треугольная призма
Эта фигура относится к классу призм, поэтому она, как любой представитель этого класса, состоит из двух одинаковых и параллельных оснований и параллелограммов. Основаниями являются треугольники произвольного типа (равносторонние, равнобедренные, прямоугольные и другие), боковые же стороны могут быть произвольными параллелограммами, ромбами, квадратами и прямоугольниками. Число боковых сторон равно трем. Рисунок ниже демонстрирует, о какой фигуре пойдет речь.
На этом рисунке мы видим геометрическую фигуру, которая состоит из пяти сторон, девяти ребер и шести вершин. Стороны мы уже охарактеризовали. Что касается ребер, то любое из них можно отнести к одному из двух типов: либо ребро принадлежит одному из оснований (в этом случае оно является стороной треугольного основания), либо оно образовано пересечением боковых граней (боковое ребро). Важным свойством призмы является равенство всех ее боковых ребер.
Все треугольные призмы классифицируются по двум признакам:
- прямые и наклонные;
- правильные и неправильные.
Прямая призма обладает прямоугольными боковыми сторонами. Если ее основания будут равносторонними треугольниками, тогда она будет правильной. Далее мы приведем формулы объема призмы треугольной прямой, правильной фигуры, призмы с прямоугольным треугольником и фигуры наклонной.
Видео:№244. Основанием пирамиды DABC является прямоугольный треугольник ABC, у которого гипотенузаСкачать
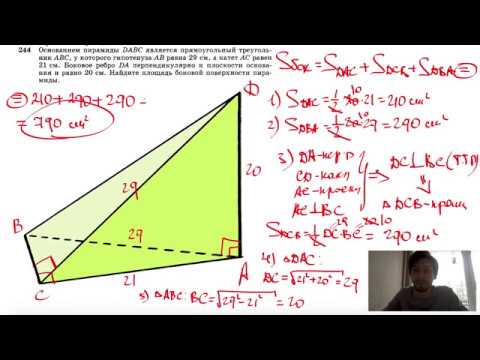
Площадь поверхности
Чтобы понять, о чем идет речь, проще всего рассмотреть развертку этой призмы. Она показана на рисунке.
Видно, что для определения площади всех сторон рассматриваемой фигуры необходимо рассчитать отдельно площадь четырехугольника и площадь шестиугольника, затем умножить их на соответствующие целые числа, равные количеству каждого n-угольника в призме, и сложить полученные результаты. Шестиугольников 2, прямоугольников 6.
Для площади прямоугольника получаем:
Тогда площадь боковой поверхности равна:
Для определения площади шестиугольника проще всего воспользоваться соответствующей формулой, которая имеет вид:
Подставляя в это выражение число n равное 6, получаем площадь одного шестиугольника:
Это выражение следует умножить на два, чтобы получить площадь оснований призмы:
Остается сложить Sos и S2, чтобы получить полную площадь поверхности фигуры:
Видео:Равносторонний треугольник в окружностиСкачать

Виды фигуры
Пирамида – геометрическая фигура, обозначающая и представляющая собой несколько граней. По сути – это тот же многогранник, в основании которого лежит многоугольник, а по бокам расположены треугольники, соединяющиеся в одной точке – вершине. Фигура бывает двух основных видов:
В первом случае, в основании лежит правильный многоугольник. Тут все боковые поверхности равны между собой и сама фигура порадует глаз перфекциониста.
Во втором случае, оснований два – большое в самом низу и малое между вершиной, повторяющее форму основного. Иными словами – усечённая пирамида представляет собой многогранник с сечением, образованным параллельно основанию.
Видео:🔴 В основании прямой призмы лежит прямоугольный ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 16 | ШКОЛА ПИФАГОРАСкачать

Найти объем призмы, зная площадь основания и высоту
Видео:Формулы равностороннего треугольника #shortsСкачать

Площадь поверхности и объём
Чтобы определить объём призмы по формуле, необходимо знать площадь её основания и высоту:
Так как основанием правильной четырёхгранной призмы является квадрат со стороной a, можно записать формулу в более подробном виде:
Если речь идёт о кубе — правильной призме с равной длиной, шириной и высотой, объём вычисляется так:
Чтобы понять, как найти площадь боковой поверхности призмы, необходимо представить себе её развёртку.
Из чертежа видно, что боковая поверхность составлена из 4 равных прямоугольников. Её площадь вычисляется как произведение периметра основания на высоту фигуры:
С учётом того, что периметр квадрата равен P = 4a, формула принимает вид:
Для вычисления площади полной поверхности призмы нужно к боковой площади прибавить 2 площади оснований:
Sполн = Sбок + 2Sосн
Применительно к четырёхугольной правильной призме формула имеет вид:
Для площади поверхности куба:
Зная объём или площадь поверхности, можно вычислить отдельные элементы геометрического тела.
Видео:№252. Основанием пирамиды DABC является равнобедренный треугольник ABC, в котором АВ = АС, ВС=6 смСкачать
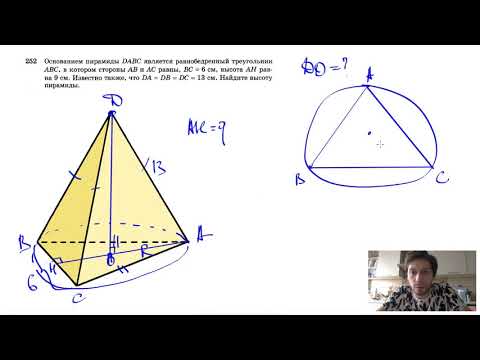
Решение простого примера
Такого вида задачи обычно даются в учебниках по геометрии для выпускных классов средней школы. Решить их самостоятельно несложно, нужно только знать формулы и представлять, как выглядит та или иная фигура. При этом часто приходится использовать дополнительные построения. Вот один из таких типовых примеров.
Пусть имеется девятиугольная фигура, в которую вписана правильная шестиугольная призма со стандартным обозначением вершин. Сторона основания в ней составляет 4 см, а длина бокового ребра меньше её в 2 раза, то есть равняется 2. Необходимо вычислить расстояние от точки C1 до прямой, соединяющей вершины EF. По условию задачи в основании лежит геометрическое тело, у которого все стороны и углы равны, то есть фигура правильная.
Чтобы понять, что будет представлять искомая прямая, нужно изобразить призму на рисунке и на нём же начертить отрезок. Фактически это будет перпендикуляр, который и является вычисляемым расстоянием. Проекцией точки С1 будет вершина С. Из неё можно построить перпендикуляр, который ограничится точкой E. Таким образом, поставленная задача сводится к поиску длины отрезка C1E.
Найти длину прямой можно как гипотенузу прямоугольного треугольника С1СE. Треугольная фигура будет с прямым углом C. Из условия задачи отрезок С1С в два раза меньше ребра основания, а значит равен 2. Теперь осталось найти, чему равняется длина CE. Геометрическое тело CDE является равнобедренным. По условию CD = ED. Сумму углов шестиугольника можно найти по формуле е = 180 * (n — 2) = 180 * 4 = 720. Получается, что на каждый угол приходится по 120 градусов.
С вершины D можно опустить перпендикуляр DN на CE. Принимая во внимание свойства равнобедренного треугольника, высота DN будет медианной и биссектрисой. Следовательно, угол C равняется 30 градусов, так как CDH — прямоугольный.
Теперь можно найти СH. Сделать это возможно через косинус угла C: cos 30 = CH / CD. Отсюда: CH = 4 * p/2 = 2 √ 3. Так как CH = HE, сторона CE = 2 * 2 √3. К треугольнику CC1E можно применить теорему Пифагора: C1E 2 = C1C 2 + CE = 2 2 + (4 c3) 2 . C1E 2 = √ 52. Таким образом, искомый ответ можно записать так: C1E = 2√13.
Видео:Геометрия Основание прямой призмы служит равнобедренный треугольник с углом 45 приСкачать

Элементы правильной четырехугольной призмы
- Основания ABCD и A1B1C1D1 равны и параллельны друг другу
- Боковые грани AA1D1D, AA1B1B, BB1C1C и CC1D1D, каждая из которых является прямоугольником
- Боковая поверхность – сумма площадей всех боковых граней призмы
- Полная поверхность – сумма площадей всех оснований и боковых граней (сумма площади боковой поверхности и оснований)
- Боковые ребра AA1, BB1, CC1 и DD1.
- Диагональ B1D
- Диагональ основания BD
- Диагональное сечение BB1D1D
- Перпендикулярное сечение A2B2C2D2 .
Видео:№251. Основанием пирамиды DABC является прямоугольный треугольник с гипотенузой ВС. БоковыеСкачать

Как выглядит призма
Правильной четырёхугольной призмой называется шестигранник, в основаниях которого находятся 2 квадрата, а боковые грани представлены прямоугольниками. Иное название для этой геометрической фигуры — прямой параллелепипед.
Рисунок, на котором изображена четырёхугольная призма, показан ниже.
На картинке также можно увидеть важнейшие элементы, из которых состоит геометрическое тело. К ним принято относить:
Основы призмы — квадраты LMNO и L₁M₁N₁O₁.
- Боковые грани — прямоугольники MM₁L₁L, LL₁O₁O, NN₁O₁O и MM₁N₁N, расположенные под прямым углом к основаниям.
- Боковые рёбра — отрезки, расположенные на стыке между двумя боковыми гранями: M₁M, N₁N, O₁O и L₁L. Также выполняют роль высоты (поскольку лежат в параллельной основаниям плоскости). В призме боковые рёбра всегда равны между собой — это одно из важнейших свойств этого геометрического тела.
- Диагонали, которые, в свою очередь, подразделяются ещё на 3 категории. К ним относится 4 диагонали основания (MO, N₁L₁), 8 диагоналей боковых граней (ML₁, O₁L) и 4 диагонали призмы, начала и концы которых являются вершинами 2 разных оснований и боковых сторон (MO₁, N₁L).
Иногда в задачах по геометрии можно встретить понятие сечения. Определение будет звучать так: сечение — это все точки объёмного тела, принадлежащие секущей плоскости. Сечение бывает перпендикулярным (пересекает рёбра фигуры под углом 90 градусов). Для прямоугольной призмы также рассматривается диагональное сечение (максимальное количество сечений, которых можно построить — 2), проходящее через 2 ребра и диагонали основания.
Если же сечение нарисовано так, что секущая плоскость не параллельна ни основам, ни боковым граням, в результате получается усечённая призма.
Для нахождения приведённых призматических элементов используются различные отношения и формулы. Часть из них известна из курса планиметрии (например, для нахождения площади основания призмы достаточно вспомнить формулу площади квадрата).
Видео:🔴 В основании прямой призмы лежит ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 16 | ШКОЛА ПИФАГОРАСкачать

Как рассчитывать объем фигуры произвольного типа?
Часть пространства, которая ограничена плоскими сторонами геометрической фигуры, называется ее объемом. В общем случае для призмы абсолютно любого типа справедлива следующая формула для определения ее объема:
Как видно, она очень проста и содержит всего два множителя: So — площадь одного основания, h — высота призмы, то есть дистанция между ее основаниями.
Применительно к треугольной призме произвольной формы (наклонной и неправильной), для вычисления величины So можно воспользоваться универсальной формулой для треугольника:
Здесь a — сторона треугольника, ha — высота треугольника, опущенная на сторону a.
Расчет высоты h призмы можно провести с использованием теоремы Пифагора, если знать длину бокового ребра b и двугранные углы между основанием и боковыми гранями.
Видео:Геометрия Основание прямой призмы – прямоугольный треугольник с катетами 15 см и 20 смСкачать

Задачи на расчет треугольной призмы
Задача 1. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, боковое ребро равно 5. Найдите объем призмы.
Решение: Объем прямой призмы равен V = Sh, где S — площадь основания, а h — боковое ребро. Площадь основания в данном случае это площадь прямоугольного треугольника (его площадь равна половине площади прямоугольника со сторонами 6 и 8). Таким образом, объём равен:
V = 1/2 · 6 · 8 · 5 = 120.
Задача 2.
Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Объем отсеченной треугольной призмы равен 5. Найдите объем исходной призмы.
Решение:
Объём призмы равен произведению площади основания на высоту: V = Sосн ·h.
Треугольник, лежащий в основании исходной призмы подобен треугольнику, лежащему в основании отсечённой призмы. Коэффициент подобия равен 2, так как сечение проведено через среднюю линию (линейные размеры большего треугольника в два раза больше линейных размеров меньшего). Известно, что площади подобных фигур соотносятся как квадрат коэффициента подобия, то есть S2 = S1k 2 = S12 2 = 4S1.
Площадь основания всей призмы больше площади основания отсечённой призмы в 4 раза. Высоты обеих призм одинаковы, поэтому объем всей призмы в 4 раза больше объема отсечённой призмы.
Общая теория
Призмой является любой многогранник, боковые стороны которого имеют вид параллелограмма. При этом в ее основании может оказаться любой многогранник – от треугольника до n-угольника. Причем основания призмы всегда равны друг другу. Что не относится к боковым граням — они могут существенно различаться по размерам.
При решении задач встречается не только площадь основания призмы. Может потребоваться знание боковой поверхности, то есть всех граней, которые не являются основаниями. Полной поверхностью уже будет объединение всех граней, которые составляют призму.
Иногда в задачах фигурирует высота. Она является перпендикуляром к основаниям. Диагональю многогранника является отрезок, который соединяет попарно две любые вершины, не принадлежащие одной грани.
Следует отметить, что площадь основания прямой призмы или наклонной не зависит от угла между ними и боковыми гранями. Если у них одинаковые фигуры в верхней и нижней гранях, то их площади будут равными.
Призма в геометрии
Изучение объемных фигур является задачей стереометрии – важной части пространственной геометрии. В стереометрии под призмой понимают такую фигуру, которая образована параллельным переносом произвольного плоского многоугольника на определенное расстояние в пространстве. Параллельный перенос предполагает такое перемещение, при котором поворот вокруг оси, перпендикулярной плоскости многоугольника, полностью исключен.
В результате описанного способа получения призмы образуется фигура, ограниченная двумя многоугольниками, имеющими одинаковые размеры, лежащими в параллельных плоскостях, и некоторым числом параллелограммов. Их количество совпадает с числом сторон (вершин) многоугольника. Одинаковые многоугольники называются основаниями призмы, а площадь их поверхности – это площадь оснований. Параллелограммы, соединяющие два основания, образуют боковую поверхность.
Площадь правильной шестиугольной призмы
Основание: правильный шестиугольник














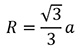










 Основы призмы — квадраты LMNO и L₁M₁N₁O₁.
Основы призмы — квадраты LMNO и L₁M₁N₁O₁.



