Биссектрисы в равностороннем треугольнике теорема

В данной публикации мы рассмотрим основные свойства биссектрисы равностороннего треугольника, а также разберем пример решения задачи по данной теме.

Примечание: напомним, что равносторонним называется треугольник, в котором равны как все стороны, так и все углы.

Видео:ОГЭ 16🔴Скачать

Свойства биссектрисы равностороннего треугольника

Свойство 1

Любая биссектриса равностороннего треугольника одновременно является и медианой, и высотой, и серединным перпендикуляром.

BD – биссектриса угла ABC, которая также является:

• высотой, опущенной на сторону AC;
• медианой, делящей сторону AC на два равных отрезка (AD = DC);

Свойство 2

Все три биссектрисы равностороннего треугольника равны между собой.

Свойство 3

Биссектрисы равностороннего треугольника в точке пересечения делятся в отношении 2:1, считая от вершины.

Свойство 4

Точка пересечения биссектрис равностороннего треугольника является центром описанной и вписанной окружностей.

• r – радиус вписанной окружности;
• R – радиус описанной окружности;
• R = 2r.

Свойство 5

Биссектриса равностороннего треугольника делит его на два равновеликих (равных по площади) прямоугольных треугольника.

Примечание: Три биссектрисы равностороннего треугольника делят его на 6 равновеликих прямоугольных треугольников.

Свойство 6

Любая из внешних биссектрис угла равностороннего треугольника параллельна стороне, лежащей напротив данного угла.

• AD и AE – внешние биссектрисы, параллельные BC;
• BK и BL – внешние биссектрисы, параллельные AC;
• CM и CN – внешние биссектрисы, параллельные AB.

Свойство 7

Длину биссектрисы ( l_a ) равностороннего треугольника можно выразить через его сторону.

где a – сторона треугольника.

Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Пример задачи

Радиус вписанной в равносторонний треугольник окружности равен 4 см. Найдите длину его стороны.

Решение

Согласно Свойствам 3 и 4, рассмотренным выше, радиус вписанной окружности составляет 1/3 часть от биссектрисы равностороннего треугольника. Следовательно, вся ее длина равняется 12 см (4 см ⋅ 3).

Теперь мы можем найти сторону треугольника с помощью формулы ниже (получена из Свойства 7):

Видео:Известна биссектриса равностороннего треугольника. Найти сторону этого треугольника. ОГЭ №16Скачать

Теорема о биссектрисе треугольника. Доказательство

Теорема 1. Биссектриса при вершине треугольника делит противоположную сторону на две отрезки, пропорциональные сторонам, прилежащим к данной вершине. То есть если биссектриса при вершине A делит в точке D сторону BC на отрезки BD и CD (Рис.1), то имеет место следующее соотношение:

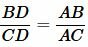(1)

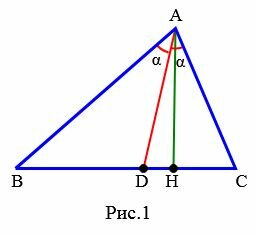Доказательство (метод площадей 1). Из вершины A опущена биссектриса AD. Построим вершину треугольника AH. Найдем площади треугольников ABD и ACD:

,

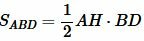(3)

.

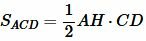(4)

Построим следующее соотношение

.

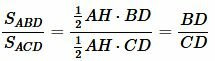(5)

С другой стороны, площадь треугольников ABD и ACD можно найти используя следующие формулы:

.

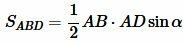(6)

.

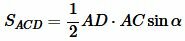(7)

Построим следующее соотношение используя формулы (6) и (7):

.

(8)

Из формул (5) и (8) получим соотношение (1).

Доказательство (метод площадей 2). С одной стороны, аналогично вышеизложенному имеем соотношение (5). Далее из точки D проведем вершины L и M для треугольников ABD и ACD (Рис.2).

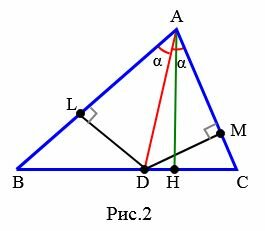Тогда площади треугольников ABD и ACD можно найти из формул:

,

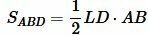(9)

.

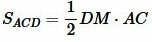(10)

Построим следующее соотношение

.

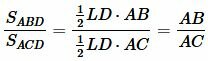(11)

Из формул (5) и (11) получим соотношение (1).

Доказательство (через теорему синусов). Рассмотрим треугольник ABC. Из точки A проведем биссектрису AD (Рис.3):

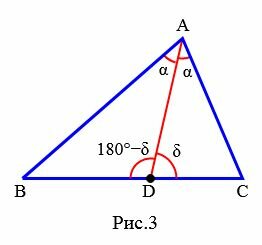Применяя теорему синусов для треугольников ABD и ACD можем записать:

,

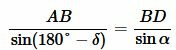(12)

.

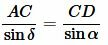(13)

Поделив (12) на (13) и учитывая, что ( small sin(180°-delta)=sin delta , ) (см. статью Формулы приведения тригонометрических функций онлайн) получим равенство (1).

Доказательство (через подобие треугольников). Рассмотрим треугольник ABC. Из точки A проведем биссектрису AD (Рис.4). Проведем перпендикуляры из вершин B и C на луч AD и обозначим точки пересечения через L и K.

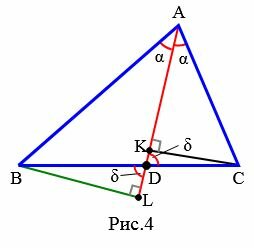Рассмотрим треугольники ABL и ACK. Эти треугольники подобны по двум углам (( small ∠ ALB= ∠ AKC ,;; ∠ BAL= ∠ CAK ) ). Тогда имеем:

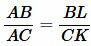(14)

Рассмотрим, далее, треугольники BLD и CKD. Они также подобны поскольку ( small ∠ BLD= ∠ CKD ,) а углы BDL и CDK равны так как они вертикальные. Тогда имеет место следующее соотношение:

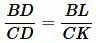(15)

Из равенств (14) и (15) получаем:

.

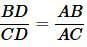Пример. Даны стороны треугольника ABC: AB=18, AC=6, BC=20. Найти отрезки, полученные делением биссектрисей большой стороны треугольника.

Решение. Поскольку напротив самой большой стороны треугольника находится вершина A, то бисскетриса AD делит сторону BC на отрезки BD и CD. Тогда имеем:

.

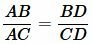(16)

Обозначим BD=x. Тогда CD=BC−x=20−x. Подставляя данные в уравнение (16), получим:

.

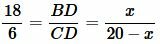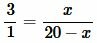(17)

Методом перекресного умножения упростим (17) и решим:

Видео:Задание 9 ОГЭ от ФИПИСкачать

Please wait.

Видео:Геометрия. 7 класс. Теоремы. Т6. Второе свойство равнобедренного треугольника.Скачать

We are checking your browser. mathvox.ru

Видео:7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать

Why do I have to complete a CAPTCHA?

Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.

Видео:7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

What can I do to prevent this in the future?

If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.

If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.

Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store.

Cloudflare Ray ID: 6dc66d052c9c1667 • Your IP : 85.95.188.35 • Performance & security by Cloudflare

🎦 Видео

Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать

Геометрия Равносторонний треугольникСкачать

Задание 15 ОГЭ. Медиана равностороннего треугольникаСкачать

Геометрия 7 класс (Урок№13 - Равнобедренный треугольник.)Скачать

Геометрия 7 класс (Урок№12 - Медианы треугольника. Биссектрисы треугольника. Высоты треугольника.)Скачать

Формулы равностороннего треугольника #shortsСкачать

Теорема о свойстве медианы равнобедренного треугольникаСкачать

Геометрия. 7 класс. Теоремы. Т5. Первое свойство равнобедренного треугольника.Скачать

Равнобедренный треугольник. Определение. Свойства. Теоремы и доказательства.Скачать

Свойства равнобедренного треугольника. 7 класс.Скачать

Равнобедренный треугольник. 7 класс.Скачать

№119. В равнобедренном треугольнике DEK с основанием DK=16см отрезок EF— биссектриса,Скачать

7 фактов про равносторонний треугольникСкачать