Читайте также:
|
Читайте также:
|
Установите соответствие между уравнениями Максвелла и их физическим смыслом. 1.  2. 2.  3. 3.  |
Укажите соответствие для каждого нумерованного элемента задания
1.Изменяющееся со временем магнитное поле порождает вихревое электрическое поле.
2. Источником вихревого магнитного поля помимо токов проводимости является изменяющееся со временем электрическое поле.
3. «Магнитных зарядов» не существует: силовые линии магнитного поля замкнуты.
Каждый из четырех одинаковых по модулю точечных зарядов (см. рис.), расположенных в вершинах квадрата, создает в точке пересечения диагоналей электрическое поле, напряженность которого равна 

Градиент потенциала поля в этой точке равен _______и направлен горизонтально …

На рисунке показана зависимость силы тока в электрической цепи от времени.

Заряд, прошедший по проводнику в интервале времени от 0 до 10 
На рисунке изображены сечения двух прямолинейных длинных параллельных проводников с одинаково направленными токами, причем 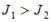

Если магнитный поток сквозь катушку из 20 витков изменяется по закону 

Уравнения Максвелла являются основными законами классической макроскопической электродинамики, сформулированными на основе обобщения важнейших законов электростатики и электромагнетизма. Эти уравнения в интегральной форме имеют вид:
1) 
2) 
3) 
4) 
Первое уравнение Максвелла является обобщением …
закона электромагнитной индукции
Установите соответствие между величиной (знаком) работы сил электростатического поля, создаваемого зарядом +Q, по перемещению отрицательного заряда –q и траекторией перемещения (указаны начальная и конечная точки).

1. А=0
2. А
Дата добавления: 2015-02-16 ; просмотров: 343 | Нарушение авторских прав
Видео:Мертвая петля - Задача ЕГЭ по физике Часть 2Скачать

Бесконечно длинный прямолинейный проводник образует плоскую петлю в виде окружности
2018-08-08 
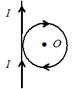
Бесконечно длинный тонкий проводник с током $I = 50 А$ имеет изгиб (плоскую петлю) радиусом $R = 10 см$. Определить в точке О магнитную индукцию $B$ поля, создаваемого этим током, в случаях а-е, изображенных на рис.
а) Закон Био — Савара Лапласа
где $d vec$ — магнитнная индукция поля создаваемого элементов проводника с током; $mu$ — магнитная проницаемость; $mu_$ — магнитная постоянная; $d vec$ — вектор, равный по модулю длине $dl$ проводника и совпадающий по направлению с током; $I$ — сила тока радиус; $vec$ -вектор, проведенный от вередины элемента проводника к точке, магнитная индукция в которой определяется.
где $alpha$ — угол между векторами $d vec$ и $vec$:
Магнитная индукция в точке О определим по принципу суперпозиции магнитных полей, создаваемых прямолинейными участками I и II и полуокружностью III
так как точка О находится на оси прямолинейных участков то для них в формуле (2) $alpha = 0; sin alpha = 0$, следовательно $B_ = B_ = 0$:
и магнитная индукция в точке О определяется полукруговым током: $B = B_$. Выделим на участке III элемент $dl$. Тогда $dB_ = frac < mu mu_> frac <r^>dl$: (в каждой точке полуокружности $alpha = pi / 2$ )
Учтя, что $r = R$ ( $R$ — радиус полукоружности ), проинтегрируем
для вакуума $mu = 1$
б) Согласно принципу суперпозиции магнитных полей результирующая магнитная индукция в точке О будет складываться из магнитных индукций, создаваемых из трех участков провода в отдельности
Все три вектора направлены в точке О в одну сторону. В силу симметрии $vec_ = vec_ Rightarrow B = 2B_+B_$
Магнитная индукция поля, создаваемого отрезком проводника
В нашем случае (рис.): $r_ = R; phi_ = frac; cos phi_ = 0; phi_ rightarrow pi; cos phi_ = 2 rightarrow B_ = frac < mu mu_> frac (0 — (-1)) = frac < mu mu_I >$.
($mu$ — магнитная постоянная, $mu_ = 4 pi cdot 10^ Гн/м$ )
Магнитная индукция поля, создаваемого круговым током в центре (точка О):
Тогда, индукция поля полукругового тока равна: $B_ = frac frac < mu mu_I > = frac < mu mu_I >$
Результирующая индукция поля в точке О:
для вакуума $mu = 1$
в) Магнитная индукция в точке О определим по принципу суперпозиции $vec = vec_ + vec_ + vec_$, где $vec_, vec_$ и $vec_$ — индукции полей, создаваемых участками 1,2 и 3 проводника соответственно т.к. точка О лежит на оси проводника 3, то $vec_ = 0$. Тогда $vec = vec_ + vec_$. Причем $vec_ uparrow uparrow vec_$. Поэтому модуль вектора $vec$ равен: $B = B_ + B_$. На основании закона Био-Савара-Лапласа индукция в центре кругового витка: $B = frac< mu_I >$ т.е. участок 2 представляет собой 3/4 окружности радиуса $R$, то $B_ = frac frac< mu_I > = frac<3 mu_I >$
Индукция поля, создаваемого отрезком проводника, равна
$B_ = frac< mu_I > ( cos phi_ = cos phi_ )$, где, как видно из рисунка $phi_ = frac ( cos phi_ = 0); phi_ rightarrow pi ( cos phi_ = — 1 )$. Поэтому
Следовательно, результирующая индукция поля в точке О:
($mu_ = 4 pi cdot 10^ Гн/м$ — магнитная постоянная)
$B = frac <4 pi cdot 10^cdot 50 > (3 cdot 3,14 + 2) = 2,86 cdot 10^ Тл$
г) В соответствии с принципом суперпозиции магнитная индукция в точке О равна:
$vec = vec_ + vec_ + vec_$, где $vec_, vec_[2]$ и $vec_$ — индукции полей, создаваемых проямолинейными участками 1,2 и 3 проводника, соответственно (рис). В силу симметрии индукции полей, создаваемых прямолинейными участками 1 и 3 проводника, в точке О равны между собой: $vec_ = vec_$. Поэтому
Векторы $vec_$ и $vec_$ в точке О направлены противоположно. Следовательно, модуль вектора $vec$:
Участок 2 проводника представляет собой окружность радиуса $R$. Магнитная индукция $B_$ в центре этого кругово витка с током определяется по формуле:
где $mu_$ — магнитная постоянная ($ mu_ = 4 pi cdot 10^ Гн/м$)
Определим индукцию поля $B_$ прямолинейного проводника. Выделим на участке 1 элемент проводника $dl$. Этот элементарный ток создает магнитное поле, модуль вектора магнитной индукции которого в точке О, согласно закону Био-Савара0Лапласа, равен:
где $r$ — расстояние от элемента $dl$ до точки О; $alpha$ — угол между векторами $d vec$ и $vec$.
$dB_ = frac < mu_I sin alpha > <4 pi R^/ sin^ alpha > frac < sin^alpha > = frac< mu_I > sin alpha d alpha$
Интегрируя в пределах от $alpha_ = 0$ до $alpha_ = frac$ получим:
$B_ = frac< mu_I > int_^ sin alpha d alpha = frac< mu_I > left . ( — cos alpha) right |_^ = frac < mu_I > ( cos 0 — cos frac ) = frac < mu_I >$, (3)
Подставим выражения (2) в (3) в формулу (1) получаем:
Так как выражение под знаком модуля отрицательно ($1 — pi 2B_$. Поэтому вектор $vec$ сонаправлен с вектором $vec_$ направлен (перпендикулярно плоскости чертежа, за чертежом).
Раскрывая энак модуля в выражении (4) получаем:
д) В соответствии с принципом суперпозиции магнитная индукция в точке О равна:
$vec = vec_ + vec_ + vec[B]_$, где $vec_, vec_$ и $vec_$ — индукции полей, создаваемых участками 1,2 и 3 проводника соответственно (рис). В силу симметрии индукции полей, создаваемых прямолинейными участками 1 и 3 проводника, в точке О равны между собой: $vec_ = vec_$. Поэтому:
Векторы $vec_$ и $vec_$ в точке О направлены в одну сторону. Следовательно направление вектора $vec$ совпадает с направлениями векторов $vec_$ и $vec_$ (перпендикулярно плоскости сертежа, на нас ), и модуль вектора $vec$ равен:
Участок 2 проводника представляет собой окружность радиуса $R$. Магнитная индукция $B_$ в центре этого кругового витка с током определяется по формуле:
где $mu_$ — магнитная постоянная ($mu_ = 4 pi cdot 10^ Гн/м$)
Определим индукцию $B_$ поля прямолинейного проводника. Выделим на участке 1 элемент проводника $dl$. Этот элементарный ток создает магнитное поле, модуль вектора магнитной индукции которого в точке О согласно закону Био-Савара-Лапласа, равен:
где $r$ — расстояние от эдемента $dl$ до точки O; $alpha$ — угол инжду векторами $d vec$ и $vec$.
$dB_ = frac < mu_I sin alpha > <4 pi R^/ sin^ alpha > frac < sin^alpha > = frac< mu_I > sin alpha d alpha$
Интегрируя в пределах от $alpha_ = 0$ до $alpha_ = frac$ получим:
$B_ = frac < mu_I > int_^ sin alpha d alpha = frac< mu_I > left . (- cos alpha) right |_^ = frac< mu_I > ( cos 0 — cos frac ) = frac< mu_I >$. (3)
Подставляя выражение (3) и (2) в формулу (1) получаем:
е) В соответствии с принципом суперпозиции магнитная индукция в точке О равна:
$vec = vec_ + vec_ + vec_$, где $vec_, vec_$ и $vec_$ — индукция полей создаеваемых участками 1,2 и 3 проводника соответственно (рис.). В силу симметрии индукции полей, создаваемых прямолинейными участками 1 и 3 проводника, в точке О равны между собой: $vec_ = vec_$. Поэтому
Векторы $vec_$ и $vec_$ в точке О направлены потивоположно. Следовательно, модуль векторы $vec$:
Участок 2 проводника представляет собой дугу, составляюшую две трети окружности радиуса $R$, т.к. $frac = 1- frac = frac$. Магнитная индукция в центре кругового витка с током определяется выражением:
Поэтому индукция $B_$ поля участка 2 проводника в точке О равна:
Определим индукцию $B_$ поля прямолинейного проводника. Выделим на участке 1 элемент проводника $dl$. Этот элементарный токслздает магнитное поле, модуль вектора магнитной индукции которого в токе О, согласно закону Био-Савара-Лапласа, равен:
где $r$ — расстояние от элемента $dl$ до точки О; $alpha$ — угол между векторами $d vec$ и $vec$; $mu_$ — магнитная постоянная ($ mu_ = 4 pi cdot 10^ Гн/м $)
Как следует из рисунка
С учетом этих соотношений формула (3) примет вид:
Интегрируя в пределах от $alpha_ = 0$ до $alpha_ = frac$ получаем:
$B_ = frac < mu_I > int_^ sin alpha d alpha = frac< mu_I > left . ( — cos alpha) right |_^ = frac< mu_I > ( cos 0 — cos frac )$
Подставляя значения $cos 0 = 1$ и $cos frac = frac < sqrt>$ получим:
Подставляя выражения (2) и (4) в формулу (1) получаем:
$B = left | frac< mu_I > left ( 1 — frac < sqrt> right ) right | = frac< mu_I > left | frac <2 — sqrt> — frac right | $, (5)
Так как выражение, стоящее под знаком модуля отрицательно $ left ( left ( frac <2 — sqrt> — frac right ) 2B_$. Поэтому вектор $vec$ сонаправлен с вектором $vec_$ (направлен перпендикулярно плоскости чертежа, за чертежом)
Раскрывая щнак модуля в выражении (5) получаем:
🎥 Видео
Магнитное поле прямолинейного проводника с током. Электромагниты и их применение. 8 класс.Скачать

Перемещение проводника в магнитное полеСкачать

Физика 11 класс (Урок№3 - Магнитная индукция. Действие магнитного поля на проводник с током.)Скачать

Проводник в магнитном полеСкачать

Действие магнитного поля на проводник с током | Физика 8 класс #25 | ИнфоурокСкачать

Действие магнитного поля на проводник с током. 8 класс.Скачать

Урок 281. Электромагнитная индукция. Магнитный поток. Правило ЛенцаСкачать

3.11-1Скачать

Урок 177 (осн). Действие магнитного поля на проводник с токомСкачать

Для чего делают печатный проводник в виде "ЗМЕЙКИ".Что такое дифференциальная параСкачать

3.235Скачать

Урок 156 (осн). Задачи на вычисление сопротивления проводника - 2Скачать

Физика 8 класс. §62 Действие магнитного поля на проводник с током. Электрический двигатель.Скачать

3.311 ир =5.30 кпиСкачать

18. Магнитное поле нескольких проводников. Заметки о магнитостатике. ч 18.Скачать

Длинная линия. Что там внутри?Скачать

17. Структура поля проводника с током. Заметки о магнитостатике. Часть 17.Скачать

 от нас
от нас (в единицах СИ).
(в единицах СИ).
 где
где  – универсальная газовая постоянная. Число вращательных степеней свободы молекулы равно …3
– универсальная газовая постоянная. Число вращательных степеней свободы молекулы равно …3 *1
*1
 . Это уравнение записано для …
. Это уравнение записано для …
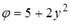 . Вектор напряженности электрического поля в точке А будет иметь направление, показанное стрелкой …
. Вектор напряженности электрического поля в точке А будет иметь направление, показанное стрелкой …

 мВб, то ЭДС индукции, возникающая в катушке в момент времени
мВб, то ЭДС индукции, возникающая в катушке в момент времени 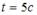 , равна …(ответ выразите в В и округлите до целых)
, равна …(ответ выразите в В и округлите до целых) ,
,  ,
,  ,
,  .
. ,
,  ,
,  ,
, 
 , то циркуляция вектора напряженности магнитного поля по контуру
, то циркуляция вектора напряженности магнитного поля по контуру  равна …
равна …








