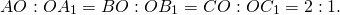Алгоритм построения медианы треугольника (6 видео)

Медиана треугольника

Что называется медианой треугольника?

Определение.

Медиана треугольника — это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

Как построить медиану треугольника?

Чтобы построить медиану треугольника , надо:

1) С помощью линейки найти и отметить середину стороны треугольника.

2) Соединить полученную точку с вершиной, лежащей напротив этой стороны.

Рисунок медианы треугольника:

Как построить медиану треугольника с помощью циркуля и линейки без шкалы, мы рассмотрим позже, в теме «Построить треугольник».

Сколько медиан имеет треугольник?

Так как у треугольника три вершины и три стороны, то и отрезков, соединяющих вершину и середину противолежащей стороны, тоже три. Значит, треугольник имеет три медианы.

Все три медианы треугольника пересекаются в одной точке:

Точка пересечения медиан называется центром тяжести треугольника.

В точке пересечения медианы треугольника делятся в отношении два к одному, считая от вершины:

Об этом свойстве медиан треугольника, а также о том, как найти длину медианы через длины сторон треугольника, более подробно мы поговорим позже и рассмотрим, как свойства медианы использовать при решении задач.

Кроме того, отдельно будут рассмотрены медиана прямоугольного треугольника, проведенная к гипотенузе и медиана равнобедренного треугольника, проведенная к его основанию, поскольку каждая из них обладает своими свойствами, которые надо знать и уметь применять.

Содержание

Пошаговое построение медианы, биссектрисы медианы в треугольнике с помощью циркуля
«Снятие эмоционального напряжения у детей и подростков с помощью арт-практик и психологических упражнений»
Геометрия. 7 класс
🎦 Видео

Видео:7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

Пошаговое построение медианы, биссектрисы медианы в треугольнике с помощью циркуля

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Видео:Геометрия 7 класс (Урок№12 - Медианы треугольника. Биссектрисы треугольника. Высоты треугольника.)Скачать

«Снятие эмоционального напряжения
у детей и подростков с помощью арт-практик
и психологических упражнений»

Сертификат и скидка на обучение каждому участнику

Медиана треугольника — это отрезок, соединяющий вершину треугольника с серединой противолежащей стороны. Поэтому, для построения медианы необходимо выполнить следующие действия:

1) найти середину стороны;

2) соединить точку, являющуюся серединой стороны треугольника, с противолежащей вершиной отрезком — это и будет медиана.

Биссектриса треугольника — это отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на противоположной стороне. Поэтому, для построения биссектрисы необходимо выполнить следующие действия:

1) построить биссектрису какого-либо угла треугольника (а биссектриса угла — это луч, выходящий из вершины угла и делящий его на две равные части);

2) найти точку пересечения биссектрисы угла треугольника с противоположной стороной;

3) соединить вершину треугольника с точкой пересечения на противоположной стороне отрезком — это и будет биссектриса.

Высота треугольника — это перпендикуляр, опущенный из вершины треугольника к прямой, содержащей противоположную сторону. Поэтому, для построения высоты необходимо выполнить следующие действия:

1) провести прямую, содержащую одну из сторон треугольника (в случае, если проводится высота из вершины острого угла в тупоугольном треугольнике);

2) из вершины, лежащей напротив проведенной прямой, опустить перпендикуляр к ней ( а перпендикуляр — это отрезок, проведенный из точки к прямой, составляющей с ней угол 90 градусов) — это и будет высота.

Задание для самостоятельной проверки.

1 вариант: Построить медиану остроугольного треугольника.

2 вариант: Построить медиану тупоугольного треугольника.

3 вариант: Построить медиану прямоугольного треугольника.

4 вариант: Построить биссектрису остроугольного треугольника.

5 вариант: Построить биссектрису тупоугольного треугольника.

6 вариант: Построить биссектрису прямоугольного треугольника.

Видео:Построение медианы в треугольникеСкачать

Геометрия. 7 класс

Конспект урока

Медианы треугольника. Биссектрисы треугольника. Высоты треугольника

Перечень рассматриваемых вопросов:

Понятие медианы, биссектрисы, высоты треугольника.
Построение медианы, высоты, биссектрисы.
Точки пересечения медианы, высоты и биссектрисы в треугольнике.
Создание представления о замечательных точках в треугольнике.

Биссектриса угла – это луч, исходящий из вершины угла и делящий его на два равных угла.

Биссектриса угла треугольника – это отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны.

Медиана треугольника – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

Высота треугольника – это перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону.

Атанасян Л. С. Геометрия: 7–9 класс. // Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. – М.: Просвещение, 2017. – 384 с.

Атанасян Л. С. Геометрия: Методические рекомендации 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А. и др. – М.: Просвещение, 2019. – 95 с.
Зив Б. Г. Геометрия: Дидактические материалы 7 класс. // Зив Б. Г., Мейлер В. М. – М.: Просвещение, 2019. – 127 с.
Мищенко Т. М. Дидактические материалы и методические рекомендации для учителя по геометрии 7 класс. // Мищенко Т. М., – М.: Просвещение, 2019. – 160 с.
Атанасян Л. С. Геометрия: Рабочая тетрадь 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А., Юдина И. И. – М.: Просвещение, 2019. – 158 с.
Иченская М. А. Геометрия: Самостоятельные и контрольные работы 7–9 классы. // Иченская М. А. – М.: Просвещение, 2019. – 144 с.

Теоретический материал для самостоятельного изучения.

Вы уже знакомы с такими понятиями как треугольник, угол, биссектриса угла.

Разберем, как построить биссектрису треугольника, а также узнаем, что такое медиана и высота треугольника.

Начнём с понятия биссектриса угла треугольника. Это отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны. AF – биссектриса ∠A треугольника ABC.

В любом треугольнике биссектрисы пересекаются в одной точке.

Введём понятие медианы треугольника.

Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.

BM – медиана треугольника ABC.

В любом треугольнике медианы пересекаются в одной точке.

Введём понятие высоты треугольника.

Перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону, называется высотой треугольника.

AH – высота треугольника ABC.

В любом треугольнике высоты или их продолжения пересекаются в одной точке.

Итак, сегодня мы узнали, какие отрезки называются медианой, биссектрисой, высотой треугольника, и научились их изображать с помощью чертёжных инструментов.

Рассмотрим, как можно решить задачу на доказательство, используя понятие «медиана треугольника».

На рисунке изображён треугольник ABC, при этом AD – медиана ∆ABC продолжена за сторону BC, так что AD = DE.

Докажем, что треугольники ABD и CED равны.

По условию в треугольниках ABD и CED: сторона AD равна стороне DE. Т. к. АD – медиана ∆ABC, то, по определению медианы, BD = DC.

∠ADB = ∠CDE (по свойству вертикальных углов).

Следовательно, ∆ABD = ∆CED (по первому признаку равенства треугольников: если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны).

Что и требовалось доказать.

Разбор решения заданий тренировочного модуля.

В треугольнике ABC проведены биссектрисы AD и BM, которые пересекаются в точке O. Найдите углы треугольника ABO, если ∠BAC = 50°, ∠ABC = 80°, а сумма углов треугольника ABO равна 180°.