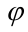Алгоритм построения линий и окружностей

В этой небольшой статье, будут рассмотрены основные виды сопряжений и Вы узнаете о том, как построить сопряжение углов, прямых линий, окружностей и дуг, окружностей с прямой.

Сопряжением называют плавный переход одной линии в другую. Для того чтобы построить сопряжение, нужно найти центр сопряжения и точки сопряжений.

Точка сопряжения – это общая точка для сопрягаемых линий. Точку сопряжения также называют точкой перехода.

Ниже будут рассмотрены основные типы сопряжений.

Видео:1 2 4 сопряжение окружностейСкачать

Сопряжение углов (Сопряжение пересекающихся прямых)

Сопряжение прямого угла(Сопряжение пересекающихся прямых под прямым углом)

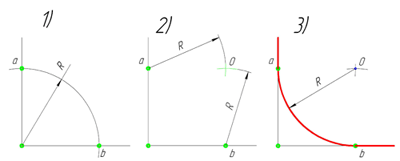
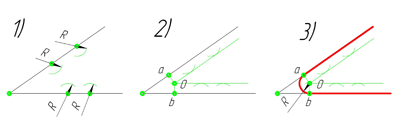
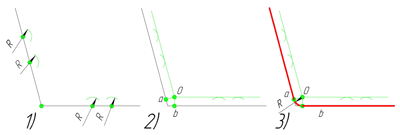
В данном примере будет рассмотрено построение сопряжения прямого угла заданным радиусом сопряжения R. Первым делом найдём точки сопряжения. Для нахождения точек сопряжения, нужно поставить циркуль в вершину прямого угла и провести дугу радиусом R до пересечения со сторонами угла. Полученные точки и будут являться точками сопряжения. Далее нужно найти центр сопряжения. Центром сопряжения будет точка равноудалённая от сторон угла. Проведём из точек a и b две дуги радиусом сопряжения R до пересечения друг с другом. Полученная на пересечении точка О и будет центром сопряжения. Теперь из центра сопряжения точки О описываем дугу радиусом сопряжения R от точки a до точки b. Сопряжение прямого угла построено.

Сопряжение острого угла(Сопряжение пересекающихся прямых под острым углом)

Ещё один пример сопряжения угла. В этом примере будет построено сопряжение
острого угла. Для построения сопряжения острого угла раствором циркуля,равным радиусу сопряжения R, проведём из двух произвольных точек на каждой стороне угла по две дуги. Затем проведём касательные к дугам до пересечения в точке О, центре сопряжения. Из полученного центра сопряжения опустим перпендикуляр к каждой из сторон угла. Так мы получим точки сопряжения a и b. Затем проведём из центра сопряжения, точки О, дугу радиусом сопряжения R, соединив точки сопряжения a
и b. Сопряжение острого угла построено.

Сопряжение тупого угла(Сопряжение пересекающихся прямых под тупым углом)

Сопряжение тупого угла строится по аналогии с сопряжением острого угла. Мы также, сначала радиусом сопряжения R проводим по две дуги из двух произвольно взятых точек на каждой из сторон, а затем проводим касательные к этим дугам до пересечения в точке О, центре сопряжения. Затем опускаем перпендикуляры из центра сопряжения к каждой из сторон и соединяем дугой, равной радиусу сопряжения тупого угла R, полученные точки a и b.

Видео:Графика с нуля | Точки и линии. Алгоритм БрезенхэмаСкачать

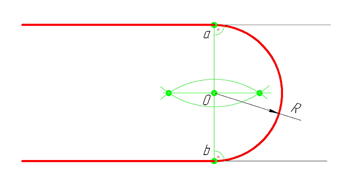
Сопряжение параллельных прямых линий

Построим сопряжение двух параллельных прямых. Нам задана точка сопряжения a, лежащая на одной прямой. Из точки a проведём перпендикуляр до пересечения его с другой прямой в точке b. Точки a и b являются точками сопряжения прямых линий. Проведя из каждой точки дугу, радиусом больш отрезка ab, найдём центр сопряжения — точку О. Из центра сопряжения проведём дугу заданного радиуса сопряжения R.

Видео:Сопряжение двух пересекающихся прямых. Урок 9. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Сопряжение окружностей(дуг) с прямой линией

Внешнее сопряжение дуги и прямой линии

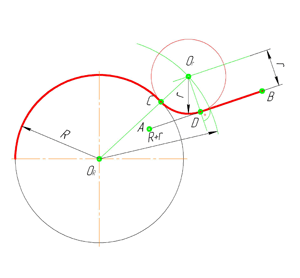
В этом примере будет построено сопряжение заданным радиусом r прямой линии, заданной отрезком AB, и дуги окружности радиусом R.

Сначала найдём центр сопряжения. Для этого проведём прямую, параллельную отрезку AB и отстоящую от него на расстояние радиуса сопряжения r, и дугу, из центра окружности O R радиусом R+r. Точка пересечения дуги и прямой и будет центром сопряжения – точкой О r .

Из центра сопряжения, точки О r , опустим перпендикуляр на прямую AB. Точка D, полученная на пересечении перпендикуляра и отрезка AB, и будет точкой сопряжения. Найдём вторую точку сопряжения на дуге окружности. Для этого соединим центр окружности О R и центр сопряжения О r линией. Получим вторую точку сопряжения – точку C. Из центра сопряжения проведём дугу сопряжения радиусом r, соединив точки сопряжения.

Внутреннее сопряжение прямой линии с дугой

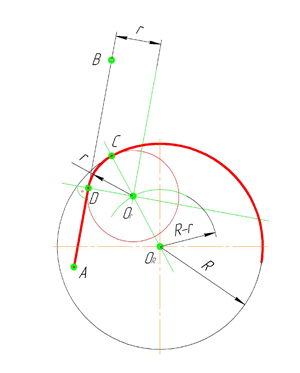
По аналогии строится внутреннее сопряжение прямой линии с дугой. Рассмотрим пример построения сопряжения радиусом r прямой линии, заданной отрезком AB, и дуги окружности радиуса R. Найдём центр сопряжения. Для этого построим прямую, параллельную отрезку AB и отстоящую от него на расстояние радиуса r, и дугу, из центра окружности O R радиусом R-r. Точка О r , полученная на пересечении прямой и дуги, и будет центром сопряжения.

Из центра сопряжения(точка О r ) опустим перпендикуляр на прямую AB. Точка D, полученная на основании перпендикуляра, и будет точкой сопряжения.

Для нахождения второй точки сопряжения на дуге окружности, соединим центр сопряжения Оr и центр окружности О R прямой линией. На пересечении линии с дугой окружности получим вторую точку сопряжения – точку C. Из точки О r , центра сопряжения, проведём дугу радиусом r, соединив точки сопряжения.

Видео:Лекция 2 | Компьютерная графика | Виталий Галинский | ЛекториумСкачать

Сопряжение окружностей (дуг)

Внешнее сопряжение дуг окружностей

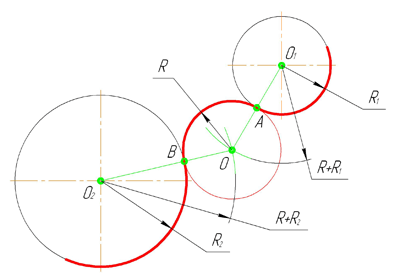
Внешним сопряжением считается сопряжение, при котором центры сопрягаемых окружностей(дуг) O1( радиус R1) и O2 (радиус R2) располагаются за сопрягающей дугой радиуса R. На примере рассмотрено внешнее сопряжение дуг. Сначала находим центр сопряжения. Центром сопряжения является точка пересечения дуг окружностей с радиусами R+R1 и R+R2, построенных из центров окружностей O1(R1) и O2(R2) соответственно. Затем центры окружностей O1 и O2 соединяем прямыми с центром сопряжения, точкой O, и на пересечении линий с окружностями O1 и O2 получаем точки сопряжения A и B. После этого, из центра сопряжения строим дугу заданного радиуса сопряжения R и соединяем ей точки A и B.

Внутреннее сопряжение дуг окружностей

Внутренним сопряжением называется сопряжение, при котором центры сопрягаемых дуг O1, радиуса R1, и O2, радиус R2, располагаются внутри сопрягающей их дуги заданного радиуса R. На картинке ниже приведён пример построения внутреннего сопряжения окружностей(дуг). Вначале мы находим центр сопряжения, которым является точка O, точка пересечения дуг окружностей с радиусами R-R1 и R-R2 проведённых из центров окружностей O1и O2 соответственно. После чего соединяем центры окружностей O1 и O2 прямыми линиями с центром сопряжения и на пересечении линий с окружностями O1 и O2 получаем точки сопряжения A и B. Затем из центра сопряжения строим дугу сопряжения радиуса R и строим сопряжение.

Смешанное сопряжение дуг окружностей

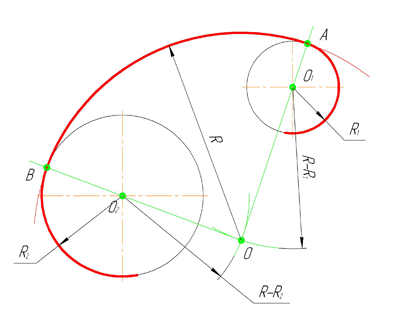
Смешанным сопряжением дуг является сопряжение, при котором центр одной из сопрягаемых дуг (O1) лежит за пределами сопрягающей их дуги радиуса R, а центр другой окружности(O2) – внутри её. На иллюстрации ниже приведён пример смешанного сопряжения окружностей. Сначала находим центр сопряжения, точку O. Для нахождения центра сопряжения строим дуги окружностей с радиусами R+R1, из центра окружности радиуса R1 точки O1, и R-R2, из центра окружности радиуса R2 точки O2. После чего соединяем центр сопряжения точку O с центрами окружностей O1 и O2 прямыми и на пересечении с линиями соответствующих окружностей получаем точки сопряжения A и B. Затем строим сопряжение.

Видео:Построение ВНЕШНЕГО СОПРЯЖЕНИЯСкачать

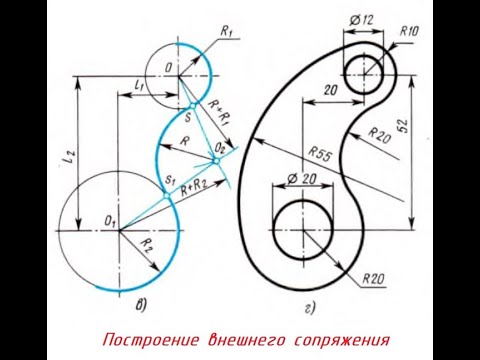
Построение линии пересечения поверхностей с примерами

Содержание:

Построение линии пересечения поверхностей:

Предложенные задания охватывают задачи не на все методы построения линий пересечения поверхностей, а только наиболее распространенные. Ниже приведены решения типовых задач, когда применены различные способы в зависимости от формы и расположения пересекающихся поверхностей.

Видео:Сопряжение окружностейСкачать

Одна из поверхностей занимает частное (проецирующее) положение

Задание: даны две поверхности:

Решение: поверхность цилиндра перпендикулярна к

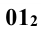
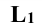
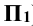
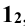
Ниже приводится построение горизонтальной проекции только одной точки 1 (рис. 13.1). Из этой точки вниз проводят линию проекционной связи. Одновременно из этой же точки радиусом проводят дугу окружности, на которой лежит эта точка, как принадлежащая тору, и находят проекцию этой окружности на горизонтальной проекции тора — это прямая линия, параллельная оси x. Она проходит через точку (точка пересечения окружности, проходящей через точку 1, с окружностью тора, лежащей на ). Горизонтальная проекция точки 1 находится на пересечении линии проекционной связи, проведенной из точки , с горизонтальной проекцией окружности тора, на которой лежит точка 1. Остальные точки строят аналогично точке 1 (рис. 13.2).

Точки 4 и 9 определяют видимость линии пересечения на горизонтальной проекции, а точки 1 и 2 наиболее удаленные от контура на горизонтальной проекции. Эту задачу можно решать и методом вспомогательных секущих плоскостей, который рассматривается далее.

Видео:Черчение. Внутреннее, внешнее и смешенное сопряжение двух окружностей.Скачать

Метод вспомогательных секущих плоскостей

Этот метод применяется для построения линии пересечения двух поверхностей, когда секущие (параллельные) плоскости при пересечении с данными поверхностями образуют простые для построения линии (прямую или окружность).

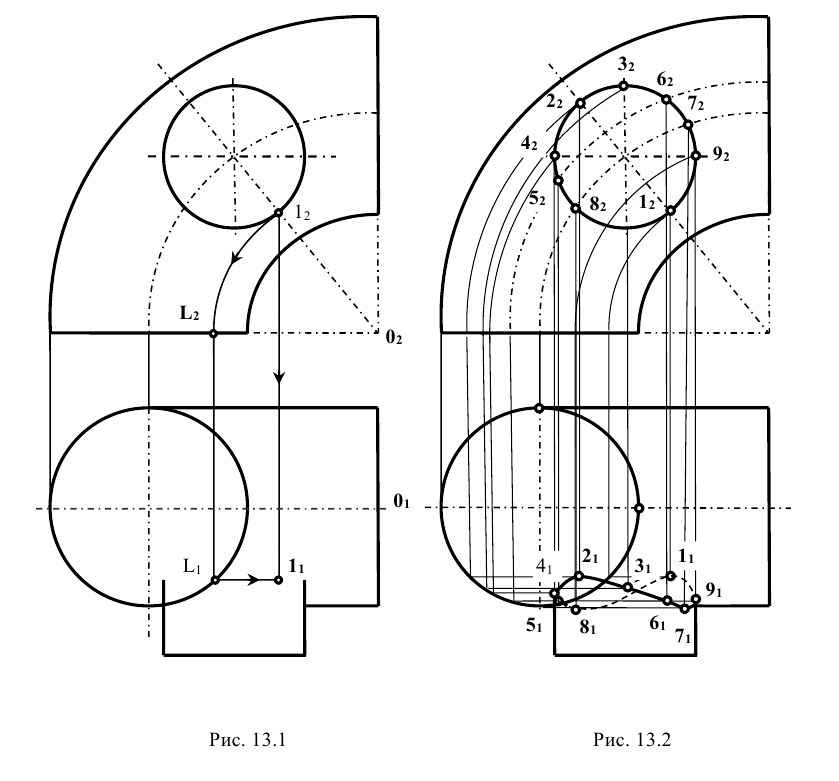
Задание: даны поверхности конуса 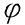и цилиндра Ф (рис. 13.3). Требуется построить линию их пересечения.

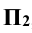
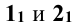
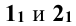
Решение: ось цилиндра перпендикулярна к плоскости , следовательно, поверхность цилиндра — проецирующая. В этом случае задача может быть решена так, как это было разобрано в предыдущем (п. 13.1.1) примере. Для этого определяют характерные -наивысшую и низшую точки линии пересечения 1 и 2, лежащие на пересечении фронтальной проекции цилиндра с очерковой образующей конуса. Их горизонтальные проекции принадлежат горизонтальной проекции очерковой образующей конуса (, совпадают с осевой линией конуса). Точки 3 и 4 определяют видимость линий пересечения на горизонтальной проекции.

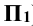
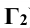
Для определения их горизонтальных проекций через ось цилиндра параллельно проводят вспомогательную секущую плоскость Г (ее фронтальный след ).

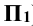
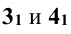
Эта плоскость рассечет цилиндр по очерковым образующим, а конус по окружности радиуса R, которая на будет проецироваться в натуральную величину. Пересечение этой окружности с очерковыми образующими цилиндра есть не что иное, как горизонтальные проекции характерных точек (рис. 13.3).

Построение промежуточных точек аналогично построению точек 3 и 4, только образующие, по которым вспомогательная плоскость будет рассекать цилиндр, не будут очерковыми (рис. 13.4).

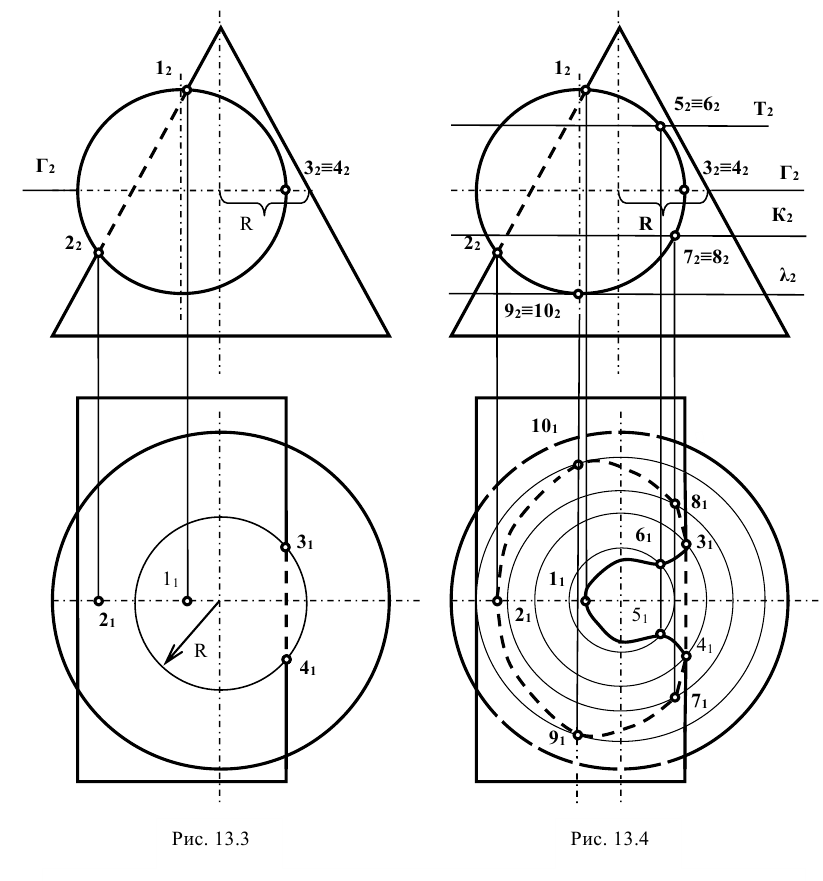
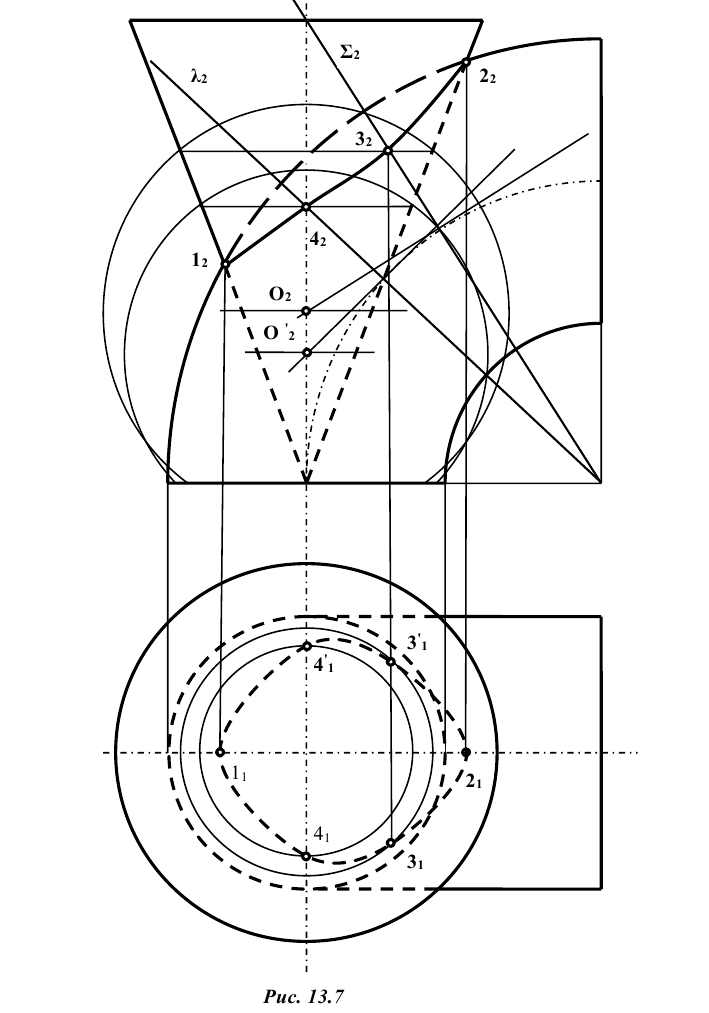
Задание: Даны две поверхности вращения — конус и цилиндр, оси которых пересекаются и находятся в одной плоскости, параллельной 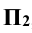(рис. 13.5). Требуется построить линию их пересечения.

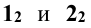
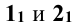
Решение: на фронтальной проекции фиксируют точки пересечения заданных поверхностей вращения — они принадлежат искомой линии пересечения. Горизонтальные проекции этих точек находятся на осевой линии конуса и цилиндра – .

Другие точки линии пересечения можно построить, используя концентрические сферические поверхности. Из точки пересечения осей фронтальных проекций, как из центра, проводятся сферы. Первая — касательная к проекции конуса, а последующие — большим радиусом (рис. 13.6). Каждая сфера пересекает обе поверхности по окружностям, фронтальные проекции которых изображаются отрезками прямых линий. Эти проекции пересекаются в точках, являющихся фронтальными проекциями точек искомой линии пересечения поверхностей.

Горизонтальные проекции этих точек определяются по принадлежности одной из поверхностей. В данном случае удобнее их получать по принадлежности конусу. Например, точки 3 и 4 лежат на той же окружности, по которой вспомогательная сфера пересекает конус. Изменяя радиус вспомогательной секущей сферы, находят ряд точек линии пересечения, соединив которые, получают проекции искомой линии (рис. 13.6). Чтобы определить видимость горизонтальной проекции линии пересечения, на её фронтальной проекции отмечают точки, лежащие на проекции осевой линии цилиндра и принадлежащие линии пересечения.

Затем по линиям проекционной связи переносят их на очерковые образующие горизонтальной проекции цилиндра. Точки, лежащие ниже указанных, будут находиться на невидимой части цилиндра.

Видео:Алгоритмы. Пересечение окружностейСкачать

Метод эксцентрических сфер

Метод эксцентрических сфер применяется для построения линии пересечении поверхностей вращения, у которых оси расположены в одной плоскости, являющейся плоскостью симметрии. При этом пересекающиеся поверхности должны иметь семейство круговых сечений.

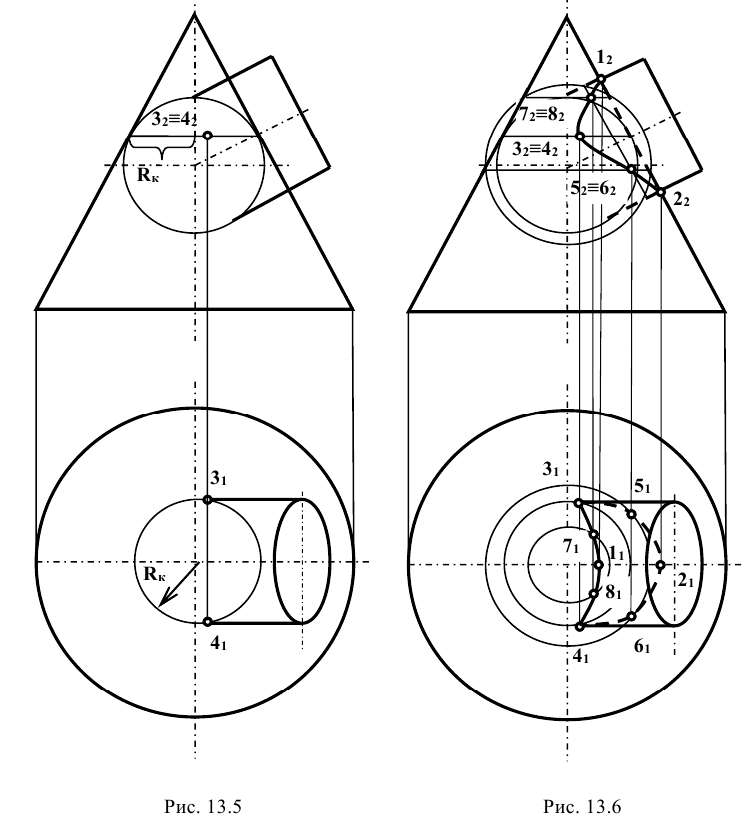
Задание: даны две поверхности вращения — тор и конус, оси которых находятся в одной плоскости, параллельной 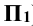(рис. 13.7). Требуется построить линии их пересечения.

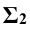
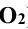
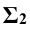
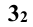
Решение: прежде всего, фиксируют опорные точки пересечения очерковых меридианов 1 и 2. Затем через ось вращения поверхности кольца проводят фронтальный след фронтально проецирующей плоскости Σ. Линия пересечения её с поверхностью тора — окружность. Центр сферы, пересекающей кольцо по окружности, находится на перпендикуляре, восстановленном из центра такой окружности к секущей проецирующей плоскости. Чтобы конус пересекался вспомогательной секущей сферой по окружности, её центр должен находиться на оси конуса. Точка пересечения перпендикуляра к проецирующей плоскости с осью конуса () выбирается центром вспомогательной секущей сферы. Радиус ее равен расстоянию от центра до точки пересечения меридиана тора со следом плоскости . Такая вспомогательная секущая сфера пересекает кольцо и конус вращения по окружностям, фронтальные проекции которых — проекции прямых. Точка пресечения этих отрезков (рис. 13.7) принадлежит искомой линии пересечения поверхностей.

Вспомогательные сферы имеют различные центры на оси конуса вращения; так, при построении проекции — точки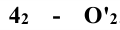. Горизонтальные проекции точек пересечения строят по принадлежности этих точек к одной из поверхностей, используя параллели, например, конуса.

Видео:Внутреннее сопряжение двух дуг окружностей третьей дугой. Урок14.(Часть1.ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Пересечение линии с поверхностью

В общем случае для графического определения положения точек пересечения линии с поверхностью необходимо выполнить ряд геометрических построений в следующей последовательности: заключить линию во вспомогательную поверхность; определить линию пересечения этой поверхности с заданной поверхностью; отметить точки пересечения построенной линии с заданной.

Этот алгоритм является универсальным, пригодным для решения любых задач. Ранее (лекция 4, рис. 4.5 и 4.6) он применялся для построения проекций точки пересечения прямой с плоскостью, где в качестве вспомогательной секущей поверхности использовалась плоскость и строилась прямая линии пересечения ее с заданной плоскостью, а искомая проекция точки пересечения определялась как место пересечения этой линии с заданной прямой.

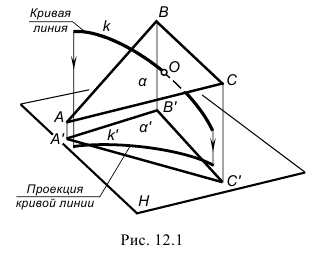
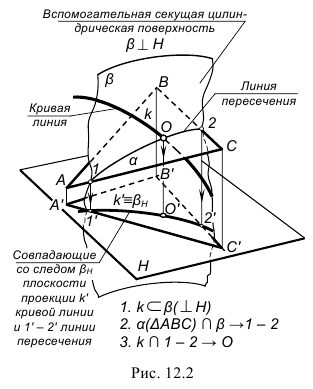
На рис. 12.1–12.3 проиллюстрирован тот же алгоритм применительно к построению точки пересечения кривой линии k с плоскостью α(∆ABC).

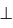
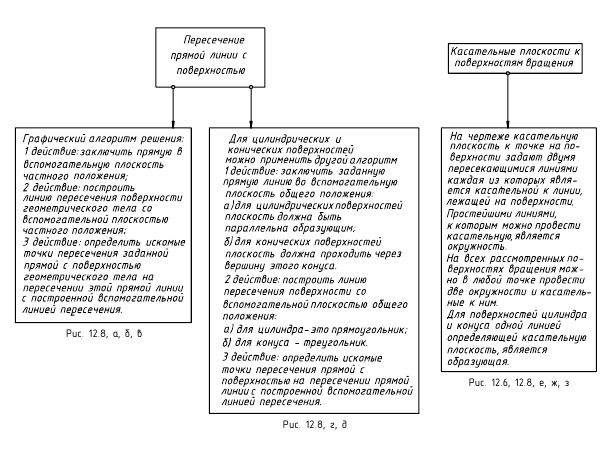
В качестве секущей поверхности в данном случае следует использовать проецирующую цилиндрическую поверхность, в частности, горизонтально-проецирующую β(β_H)H, в которую должна быть заключена кривая k(k»,k’). Для этого на чертеже (рис. 12.3) обозначаем горизонтальный след этой поверхности β_H. Горизонтальная проекция линии ее пересечения с заданной плоскостью α(∆ABC) совпадает с ним, располагаясь между точками 1′-2′. Для построения ее фронтальной проекции воспользуемся произвольными вспомогательными прямыми линиями, принадлежащими плоскости. Вначале задаем их горизонтальные проекции, например, через вершину C. Затем по точкам их пересечения со стороной AB находим фронтальные проекции вспомогательных прямых и определяем на них фронтальные проекции точек пересечения с ними заданной кривой. Проводим через найденные точки плавную кривую линию, являющуюся, таким образом, фронтальной проекцией линии пересечения, и отмечаем на ней место пересечения с фронтальной проекцией заданной кривой k(k»,k’) – точку O». Это и будет фронтальная проекция искомой точки пересечения заданной кривой k(k»,k’) с плоскостью α(∆ABC). Затем, воспользовавшись линией связи, находим горизонтальную проекцию O’ точки пересечения.

Этот алгоритм применен и для построения точек пересечения прямой линии с поверхностями геометрических тел – призмы, пирамиды и самопересекающегося тора (рис. 12.8, а, б, в). Поскольку поверхности этих тел являются замкнутыми, то необходимо найти по две точки пересечения на каждой из них.

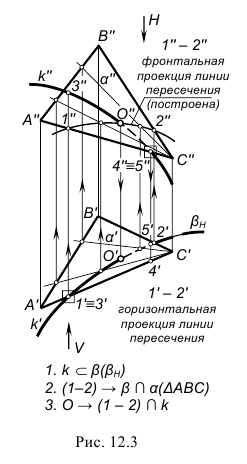
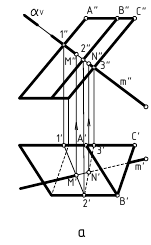
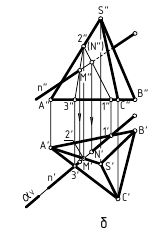
При пересечении с призмой (рис. 12.8, а) в качестве секущей плоскости для заключения в нее заданной прямой m(m»,m’) использовалась фронтально-проецирующая плоскость α_V. При пересечении с пирамидой (рис. 12.8, б) в качестве секущей плоскости для заключения в нее заданной прямой n(n»,n’) использовалась горизонтально-проецирующая плоскость α_H. При пересечении с самопересекающимся тором (рис. 12.8, в) в качестве секущей плоскости для заключения в нее заданной прямой l(l»,l’) использовалась фронтальная плоскость β_H. Далее все действия аналогичны рассмотренным. В каждом случае вначале строилась линия пересечения поверхности плоскостью, исходя из ее проецирующего положения, определялись на ней точки пересечения с заданной прямой, а при окончательном оформлении – видимость на чертеже.

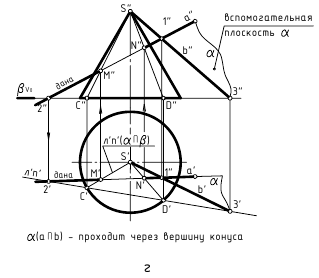
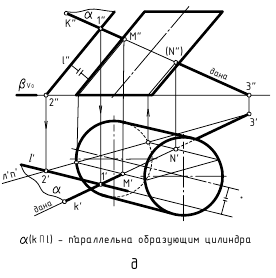
В качестве секущей плоскости при определении точек пересечения прямой с поверхностью могут использоваться также плоскости общего положения, пересекающие поверхность вдоль ее образующих (рис. 12.8, г, д). Так, для построения точек пересечения прямой a(a»,a’) общего положения с поверхностью прямого кругового конуса (рис. 12.8, г) показано использование плоскости общего положения α, проходящей через вершину конуса и заданную прямую. Плоскость задана двумя пересекающимися прямыми. Одна из них – это заданная прямая a(a»,a’), вторая – пересекающаяся с ней произвольная прямая b(b»,b’), проходящая через вершину конуса. Для построения проекций образующих, вдоль которых плоскость пересекает поверхность конуса, найден ее горизонтальный след, затем проекции C’ и D’ точек его пересечения с горизонтальным следом основания конуса и фронтальные проекции C» и D» этих точек. Искомые проекции точек M(M»,M’) и N(N»,N’) пересечения заданной прямой общего положения с поверхностью конуса находятся в местах пересечения с ней построенных образующих.

Аналогичные действия выполнены и для построения проекций M»,M’ и N»,N’ точек пересечения прямой общего положения k(k»,k’) с поверхностью наклонного эллиптического цилиндра (рис. 12.8, д). Для этого использовалось задание плоскости общего положения α(k∩l) также двумя пересекающимися прямыми, одна из которых, как и в предыдущем случае, – это заданная прямая k(k»,k’), а пересекающаяся с ней в произвольной точке 1(1″,1′) вторая прямая линия – это прямая l(l»,l’), параллельная образующим цилиндра. Строился горизонтальный след этой плоскости и по точкам пересечения его с горизонтальным следом заданного цилиндра находились образующие, по которым вспомогательная плоскость общего положения α(k∩l) пересекает цилиндр. В местах пересечения с проекциями этих образующих проекций прямой общего положения k(k»,k’) находятся искомые проекции M»,M’ и N»,N’ точек пересечения заданной прямой с поверхностью цилиндра.

Видео:Построение окружности по трём точкам.Скачать

Касательные плоскости и нормаль к поверхности

Плоскостью, касательной к поверхности в некоторой ее точке, называют плоскость, в которой можно провести две прямые линии, пересекающиеся в точке касания, касательные к двум пересекающимся в этой же точке линиям, принадлежащим поверхности.

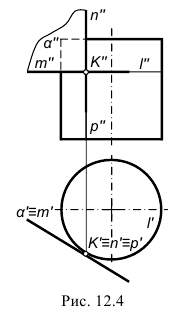
На чертеже касательную плоскость α(α»,α’) однозначно можно задать проекциями двух пересекающихся прямых m(m»,m’) и n(n»,n’). Эти линии строят касательно к проекциям двух пересекающихся в точке касания линий, принадлежащих поверхности. На рис. 12.4 линия m(m»,m’) является касательной к линии окружности l(l»,l’), проходящей через точку касания K(K»,K’) по поверхности цилиндра, а пересекающаяся с ней в этой точке линия n(n»,n’) сливается с линией р(р»,р’) – образующей цилиндра.

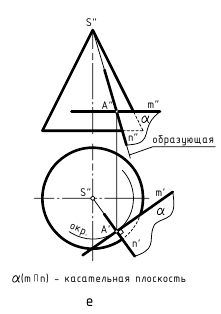
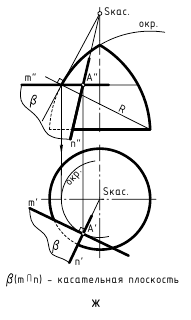
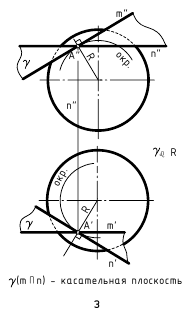
Аналогичные действия (рис. 12.8, е, ж, з) выполнены и при построении касательных плоскостей к поверхностям прямого кругового конуса, самопересекающегося тора и сферы, касающихся этих поверхностей в некоторой точке A(A»,A’). Пересекающиеся прямые m(m»,m’) и n(n»,n’), задающие касательные плоскости α(α»,α’) к ним, являются касательными к окружностям, построенным на этих поверхностях вращения и пересекающимся в точке касания A(A»,A’). Следует отметить одну особенность при построении прямой n(n»,n’), касательной к линии меридионального сечения поверхности самопересекающегося тора (рис. 12.8, ж). Для упрощения построений вначале строят касательную к этой линии, параллельной фронтальной плоскости проекций, определяют на оси вращения тора точку S, через которую проходят касательные ко всем точкам, расположенным на той же параллели поверхности, что и заданная точка касания A(A»,A’), а затем строят необходимую касательную n(n»,n’).

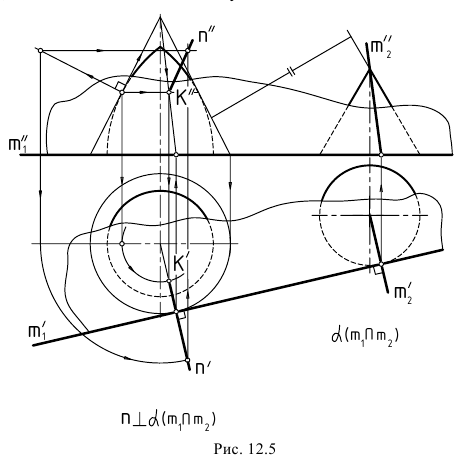
Эти построения использовались также для определения точки касания K(K»,K’) на поверхности самопересекающегося тора в задаче на рис. 12.5, где необходимо было задать общую касательную плоскость к поверхностям самопересекающегося тора и прямого кругового конуса. Ключом к решению задачи явилось заключение самопересекающегося тора в коническую поверхность с тем же углом наклона образующих, что и у заданного конуса (справа). Общая касательная плоскость задана пересекающимися прямыми, из которых m₁(m₁«,m₁‘), являющаяся горизонтальным следом плоскости, построена, как касательная к следам указанных конических поверхностей, а прямая m₂(m₂«,m₂‘), сливается с одной из образующих заданного конуса. Эта образующая является и геометрическим элементом касания построенной плоскости α(m₁∩m₂) с поверхностью заданного конуса. Поверхности самопересекающегося тора эта плоскость касается в точке K(K»,K’), которая найдена благодаря вышерассмотренным построениям и образующей второго конуса, охватывающего тор.

На рассматриваемом чертеже показано также построение нормали n(n»,n’), к поверхности самопересекающегося тора в точке K(K»,K’). Условием для построения нормали является ее перпендикулярность к плоскости, касательной к поверхности в той же точке. Вначале нормаль построена к очерковой образующей тора, затем на ней взята произвольная точка и выполнен ее поворот вокруг оси тора в положение, в котором она окажется расположенной в плоскости, перпендикулярной построенной касательной плоскости (направления указанных перемещений показаны стрелками).

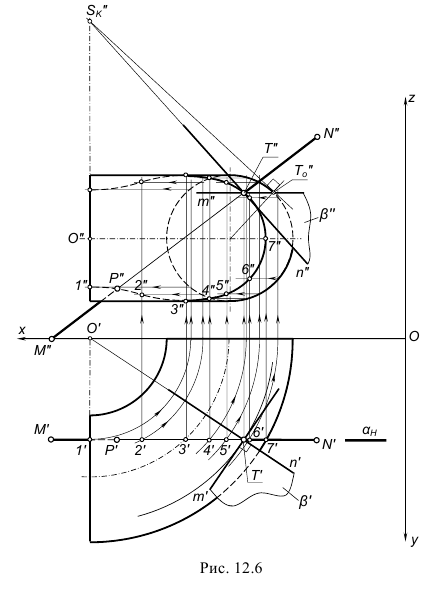
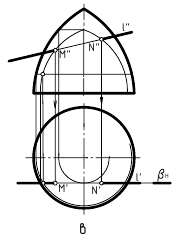
На рис. 12.6 показано построение точек пересечения P(P»,P’) и T(T»,T’) фронтальной прямой MN(M»N»,M’N’) с поверхностью ¼ кольцевого тора и построение касательной плоскости к этой поверхности в одной из построенных точек, например, T(T»,T’).

Точки P(P»,P’) и T(T»,T’) найдены благодаря заключению заданной прямой MN во фронтальную плоскость α(α_H) и построению проекций линии пересечения по точкам 1′, 2′, 3′, … , 7′, крайние из которых 1′ и 7′ взяты в местах пересечения горизонтального очерка плоскостью тора, а остальные – произвольно на горизонтальном следе α_H секущей плоскости. Для дальнейших построений использовались горизонтальные сечения поверхности тора плоскостями.

Для задания касательной плоскости β(m∩n) одна из задающих ее пересекающихся прямых m(m»,m’) построена как касательная к линии кольцевого сечения поверхности тора в точке T(T»,T’), а вторая – как касательная прямая n(n»,n’) к линии окружности осевого сечения поверхности тора. Для более точного построения второй прямой была найдена проекция S_K» точки на оси вращения тора, в которой сходятся все касательные прямые к поверхности тора во всех точках, находящихся на той же параллели, что и точка T(T»,T’).

Структуризация материала двенадцатой лекции в рассмотренном объеме схематически представлена на рис. 12.7 (лист 1). На последующем листе 2 компактно приведены иллюстрации к этой схеме для визуального закрепления изученного материала при повторении (рис. 12.8).

Пересечение линии с поверхностью:

Касательные плоскости и нормаль к поверхности

Касательная плоскость к кривой поверхности в некоторой точке – это плоскость, в которой лежат все касательные прямые ко всем кривым, которые можно провести на поверхности через ту же точку.

Нормалью к поверхности в данной точке называется прямая, перпендикулярная к касательной плоскости и проходящая через точку касания.

12.1. Пересечение прямой с поверхностью

12.2. Касательные плоскости

• Проецирование прямой
• Взаимное положение плоскостей, прямой линии и плоскости
• Взаимное расположение точки, прямых и плоскостей
• Перпендикулярность геометрических объектов
• Прямая в пространстве и ее изображение на чертеже
• Многогранники
• Поверхности вращения
• Пересечение прямой линии с поверхностью

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Видео:Построение пятиугольника циркулемСкачать

Создание и редактирование прямых и кривых линий, окружностей и дуг, прямоугольников и пазов

• Главная
• Уроки Inventor
• Создание и редактирование прямых и кривых линий, окружностей и дуг, прямоугольников и пазов

Уроки Inventor

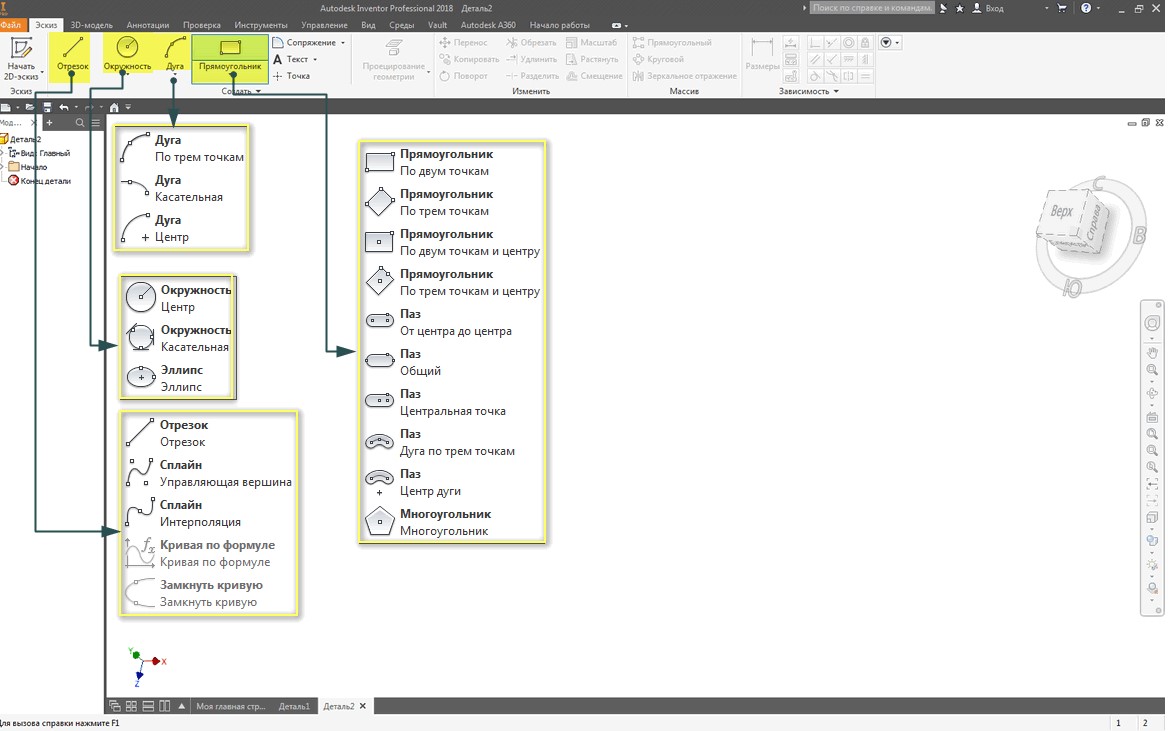
Инструменты создания геометрических примитивов эскиза расположены на вкладке Эскиз в группе команд Создать

Рисунок 1 — Инструменты создания геометрических примитивов эскиза

Видео:Построение ВНУТРЕННЕГО СОПРЯЖЕНИЯСкачать

Прямые и криволинейные линии

Создание прямолинейных элементов производится щелчком по Отрезок в группе команд Создать на вкладке 2D-эскиз

Алгоритм создание сегментов прямого отрезка:

1. Щелкнуть по кнопке Отрезок.
2. В графическом окне указать начальную точку.
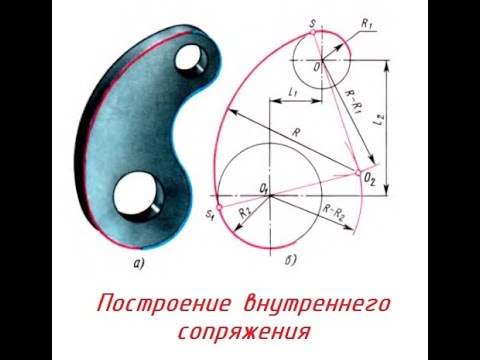
3. Выполнить несколько щелчков мышью, чтобы создавать цепочку непрерывных прямых сегментов отрезка (создадим четыре отрезка, которые понадобятся при построении окружности), или дважды щелкнуть мышью, чтобы завершить создание отрезка.
4. Для завершения проецирования нажать Esc или выбрать другую команду.

Рисунок 2 – Контекстное меню команды Отрезок

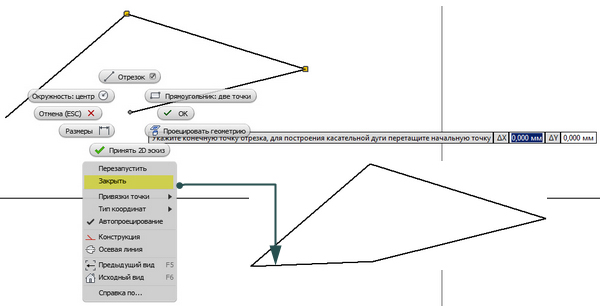
Алгоритм создания закрытого профиля

1. С помощью команды Отрезок создать эскиз с использованием двух или более отрезков.
2. После указания конечной точки предпоследнего сегмента, когда команда Отрезок еще выполняется, щелкнуть правой кнопкой мыши и выбрать Закрыть.
   Программа доводит последний сегмент линии до начальной точки профиля и замыкает профиль. Команда Отрезок остается активной.
3. Закрыть открытый профиль (замкнуть контур)

Видео:СОПРЯЖЕНИЕ ОКРУЖНОСТИ С ЛИНИЕЙ [pairing the circle with the line]Скачать

Сплайн

Сплайны – это гладкие кривые, проходящие через множество заданных точек (эскизные точки, рабочие точки, середины и конечные точки отрезков, вершины, центры дуг и окружностей) с изменением радиуса кривизны. Точки сплайна могут быть частично или полностью связаны зависимостями с другими объектами.

В Inventor поддерживаются два типа сплайнов: Сплайны с интерполяцией и Сплайны по управляющим вершинам

Рисунок 3 – Контекстное меню команды Сплайн (интерполяция)

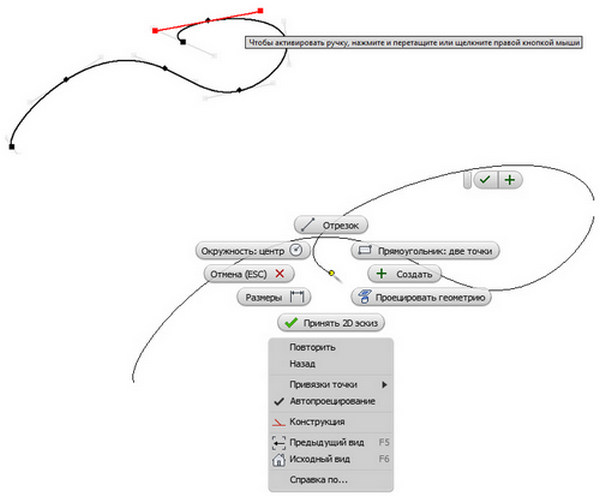
• Сплайны с интерполяцией проходят через серию точек, которые называются определяющими точками. Изменять кривую можно с помощью ручек, расположенных на точках. В графическом окне конечные точки сплайнов с интерполяцией являются квадратными, а определяющие точки вдоль кривой имеют ромбовидную форму. Сплайны с интерполяцией можно создавать как на 2D-, так и на 3D-эскизах, а также на поверхности.

Алгоритм создания сплайнов с интерполяцией

1. В активном эскизе выбрать Сплайн с интерполяцией .
2. Щелкнуть в графическом окне, чтобы задать первую точку, или выбрать существующую.
3. Выполнить ряд последовательных щелчков мышью для создания определяющих точек.
4. По завершении нажать кнопку ОК, чтобы завершить построение сплайна и закрыть команду, или нажать кнопку Создать, чтобы завершить построение сплайна и создать дополнительные сплайны.
5. Нажать кнопку ОК

Рисунок 4 – Контекстное меню команды Сплайн (управляющая вершина)

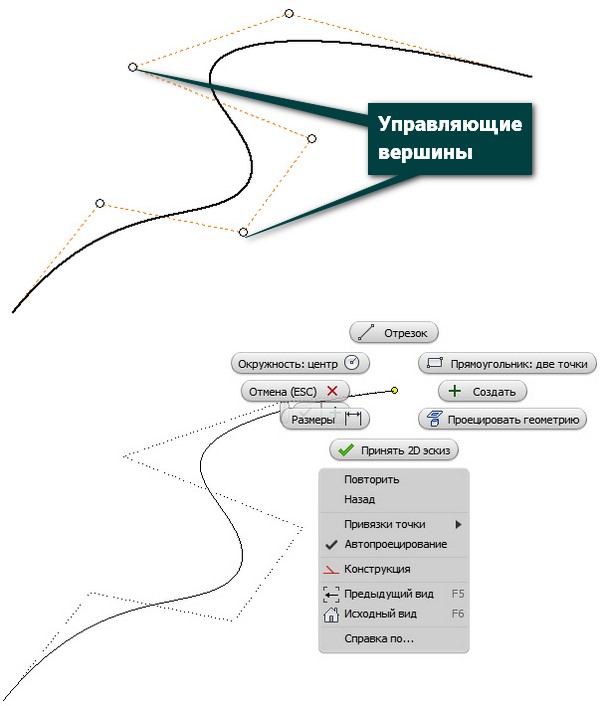
• Сплайны по управляющим вершинам – создание сплайна с помощью управляющей рамки. При создании сплайна форма и расположение отображаются как вспомогательные линии. Управляющие вершины на рамке, отображаемые как окружности, воздействуют на кривые сплайнов. Сплайн данного типа является касательным к управляющей рамке в начальной и конечной точках.

Алгоритм создания сплайнов по управляющим вершинам

1. В активном эскизе выбрать Сплайн по управляющим вершинам
2. Щелкнуть в графическом окне, чтобы задать первую точку, или выбрать существующую точку.
3. Выполнить ряд последовательных щелчков мышью для создания.
4. По завершении нажать кнопку ОК, чтобы завершить построение сплайна и закрыть команду, или нажать кнопку Создать, чтобы завершить построение сплайна и создать дополнительные сплайны.
5. Нажать кнопку ОК

Алгоритм изменения типа сплайна

1. В контекстном меню выбрать Преобразовать в сплайн по управляющим вершинам или Преобразовать в интерполяцию
   Если вернуть преобразованный сплайн к первоначальному типу, то у сплайна не будет аналогичных определяющих точек или управляющей рамки сплайна, как в исходной геометрии. При исходном преобразовании создается оптимальный сплайн, и добавляются дополнительные точки или вершины.
2. Можно изменить расположение точек

Видео:Построение эвольвенты окружностиСкачать

Окружность и эллипс

На вкладке 2D-эскиз в группе команд Создать в списке Окружность содержатся команды создания окружности и эллипса

• Окружность: центр — построение окружности с заданием центра и радиуса.
• Окружность: касательная – построение вписанной окружности, касающейся трех пересекающихся прямых.
• Эллипс – построение эллипса заданием точки центра, большой и малой оси.

Окружность

Для построения окружности необходимо выбрать грань детали или рабочую плоскость в качестве плоскости построений. Окружность может быть создана по центральной точке и радиусу, или как касательная к трем линиям:

Рисунок 5 – Создание окружности

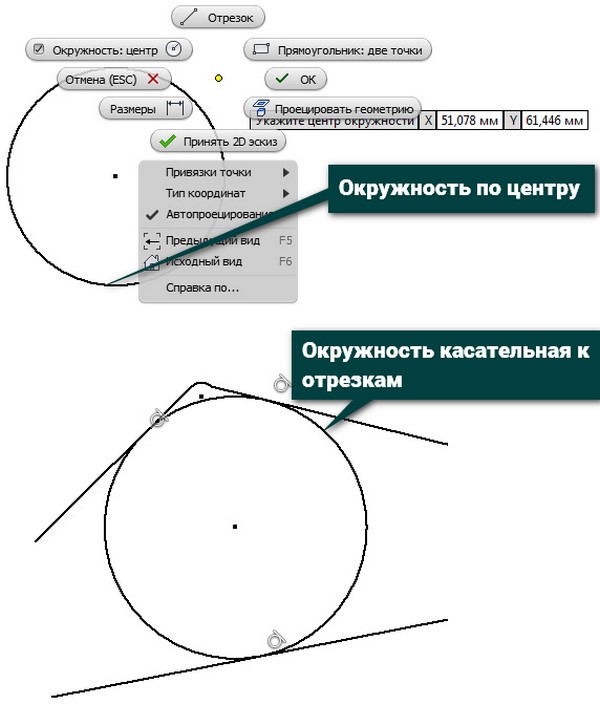
Алгоритм создания окружности

1. Щелкнуть на вкладке Эскиз в группе команд Создать выбрать способ создания окружности:
   1. Окружность: центр.
      • Первый щелчок задает центральную точку,
      • Второй щелчок определяет радиус.
      • В контекст ном меню выбрать ОК
   2. Окружность: касательная.
      • Первый щелчок задает центральную точку,
      • Второй щелчок определяет радиус. Зависимость касательности применяется в том случае, если вторая точка расположена на линии, дуге, окружности или эллипсе.
   3. Указать третью линию
   4. Щелкнуть в графическом окне, чтобы задать точки окружности или линии касательной.
2. Для завершения нажать Esc или выбрать другую команду.

Видео:Пересечение двух плоскостей. Плоскости в виде треугольникаСкачать

Эллипс

Для построения эллипса необходимо выбрать грань детали или рабочую плоскость в качестве плоскости построений. Inventor позволяет создать эллипс с помощью начала координат, большой и малой оси, определяемых пользователем. Так же как и другие кривые, эллипсы можно обрезать и удлинять.

Алгоритм создания эллипса

1. В активном эскизе выбрать Эллипс.
2. Щелкнуть в графической области для выбора центра эллипса.
3. Переместить курсор для определения направления первой оси эллипса, которая обозначена осевой линией. Щелкнуть для определения направления и длины оси.
4. Переместить курсор, указывая длину второй оси эллипса. Затем щелкнуть в нужной позиции для создания эллипса.
5. Для завершения проецирования нажать Esc или выбрать другую команду.

Видео:Метод эксцентрических сферСкачать

Дуга

На вкладке 2D-эскиз в группе команд Создать в списке Дуга содержатся команды создания дуги.

Рисунок 6 – Создание дуги

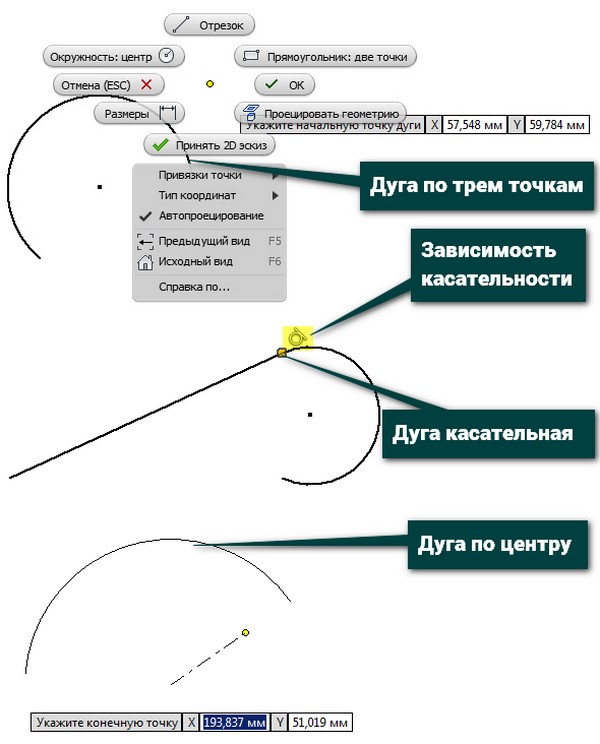
Дуга по трем точкам — создание дуги, определяемой двумя конечными точками и точкой, принадлежащей дуге. Первый щелчок определяет первую конечную точку, второй устанавливает вторую конечную точку (длину хорды), и третий щелчок показывает направление дуги и радиус.

Алгоритм создания дуги по трем точкам или началу координат:

1. В активном эскизе выбрать один из параметров:
   1. Дуга: 3 точки.
   2. Дуга: начало координат.
2. Щелкнуть в графическом окне для размещения первой точки дуги.
3. Переместить курсор по диагонали прямоугольника и указать положение противоположного угла.
4. Переместить курсор, просматривая предварительное изображение дуги, и щелкнуть для выбора конечной точки дуги.
5. Для завершения проецирования нажать Esc или выбрать другую команду.

Касательная дуга — создание дуги, касающейся заданной линии или дуги в конечной точке. Первый щелчок (на конечной точке кривой) указывает касательную конечную точку. Вторая точка указывает конец касательной дуги

Алгоритм создания касательной дуги до существующей геометрии в 2D-эскизе

1. В активном 2D-эскизе выбрать Касательная дуга .
2. Переместить курсор к концу существующей кривой, выделив конечную точку.
3. Щелкнуть рядом с конечной точкой, чтобы начать от нее построение дуги.
4. Просмотреть дугу, перемещая курсор, а затем щелкнуть кнопкой мыши, чтобы выбрать конечную точку дуги.
   Зависимость совмещения конца отрезка и дуги накладывается автоматически
5. Для завершения нажать ESC или выбрать другую команду.

Дуга по центральной точке — создание дуги, определяемой ее центральной точкой и двумя конечными. Первый щелчок устанавливает центральную точку, второй определяет радиус и начальную точку, и третья точка завершает дугу.

Видео:Построение линии пересечения поверхности конуса с проецирующей плоскостьюСкачать

Прямоугольник, многоугольник и пазы

На вкладке 2D-эскиз в группе команд Создать в списке Прямоугольник содержатся команды создания прямоугольников, многоугольников и пазов.

💡 Видео

Линия пересечения двух поверхностей конус и цилиндр (Метод секущих плоскостей)Скачать

Всё про углы в окружности. Геометрия | МатематикаСкачать