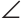Видео:№244. Отрезок AD — биссектриса треугольника ABC. Через точку D проведена прямая, параллельная АССкачать
Ваш ответ
Видео:В треугольнике ABC проведена биссектриса AD и AB=AD=CD. Найти меньший угол треугольника ABCСкачать
решение вопроса
Видео:Геометрия Отрезок AD биссектриса треугольника ABC AB = 6 см AC = 8 см угол BAC = 120 Найдите бисСкачать
Похожие вопросы
- Все категории
- экономические 43,282
- гуманитарные 33,619
- юридические 17,900
- школьный раздел 607,029
- разное 16,829
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Видео:1701 в треугольнике ABC Известно что угол bac равен 64° AD это биссектриса Найдите угол БСкачать
Свойство точек биссектрисы угла — определение и вычисление с доказательствами и примерами решения
Свойство точек биссектрисы угла:
По определению биссектриса угла делит угол пополам.
У биссектрисы есть еще одно важное свойство.
Теорема (о биссектрисе угла).
Любая точка биссектрисы угла равноудалена от сторон угла. Если точка внутри угла равноудалена от сторон угла, то она лежит на биссектрисе этого угла.
В данной теореме два утверждения: прямое и ему обратное. Докажем каждое из этих утверждений отдельно.
1) Дано: AD — биссектриса 
Доказательство:
Прямоугольные треугольники АКМ и ANM равны по гипотенузе и острому углу (гипотенуза AM — общая,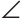 
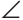
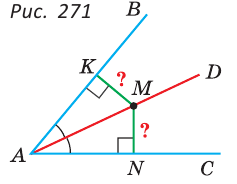
KAM =
NAM, так как AD — биссектриса). Катеты МК и MN равны как соответствующие в двух равных треугольниках.
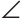
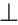
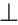
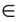
2) Дано: BAC, МК
AB, MNAC, МК = MN, M
AD (рис. 272).
Доказать: луч AD — биссектриса 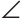BAC.
Доказательство:
Прямоугольные треугольники АКМ и ANM равны по катету и гипотенузе (гипотенуза AM — общая, МК = MN по условию). Углы КAM и NAM равны как соответствующие в двух равных треугольниках, откуда луч AD — биссектриса 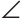BAC. Теорема доказана.
Из доказанной теоремы следует, что биссектриса является геометрическим местом точек плоскости, находящихся внутри угла и равноудаленных от сторон угла.
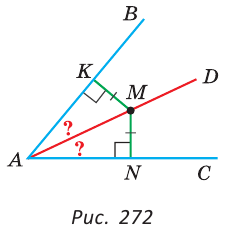
Пример:
В прямоугольном треугольнике ABC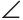 
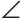
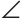
C = 90°, 
A = 40° (рис. 273). На катете АС взята точка К так, что КС=6 см и 
KBC = 25°. Найти расстояние от точки К до прямой АВ.
Решение:
Искомое расстояние равно длине перпендикуляра КМ к прямой АВ. Так как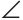 
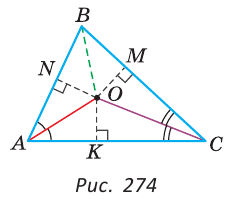
ABC = 90° —
A = 90° — 40° = 50°, то 
ABK = 50° — 25° = 25°. Следовательно, ВК — биссектриса угла ABC. Поскольку любая точка биссектрисы угла равноудалена от сторон угла, то КМ = КС = 6 см.
Пример: (2-я замечательная точка треугольника).
Доказать, что биссектрисы треугольника пересекаются в одной точке.
Доказательство:
Проведем в 
АВС биссектрисы углов А и С. Пусть О — точка их пересечения (рис. 274).
Так как точка О лежит на биссектрисе АО угла А, то она равноудалена от сторон угла А, то есть равны перпендикуляры ON и ОК к сторонам угла А. Так как точка О лежит на биссектрисе СО угла С, она равноудалена от сторон угла С, то есть равны перпендикуляры ОК и ОМ к сторонам угла С. Тогда ОК = ОМ = ON. Так как перпендикуляры ON и ОМ равны, то точка О равноудалена от сторон угла В. Точка, равноудаленная от сторон угла, лежит на биссектрисе этого угла. Поэтому биссектриса угла В пройдет через точку О, и, следовательно, все три биссектрисы пересекутся в одной точке.
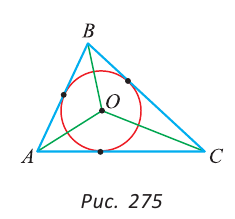
Замечание. Точка пересечения биссектрис треугольника является центром вписанной в него окружности (рис. 275), которая касается всех трех сторон треугольника (имеет с каждой из сторон только одну общую точку).
Пример:
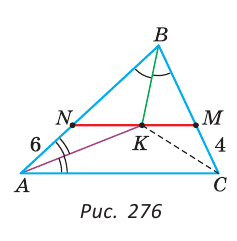
В треугольнике ABC биссектрисы углов А и В пересекаются в точке К. Через точку К проведен отрезок NM, параллельный стороне АС с концами на сторонах АВ и ВС соответственно; AN = 6 см, МС = 4 см. Найти отрезок NM.
Решение:
Так как биссектрисы треугольника пересекаются в одной точке, то СК — биссектриса угла С (рис. 276).
Треугольник ANK — равнобедренный. Действительно, 
NAK =
CAK, поскольку АК — биссектриса, 
CAK =
AKN как накрест лежащие при параллельных прямых NM и АС и секущей АК, откуда 
NAK =
AKN и треугольник ANК — равнобедренный по признаку равнобедренного треугольника. Тогда NK=AN=6 см. Аналогично доказываем, что треугольник KMC — равнобедренный и КМ=МС=4 см.
Искомый отрезок NM = NK + КМ = 6 + 4=10 (см).
Замечание. Решив задачу 3, мы доказали, что если NM || АС и отрезок NM проходит через точку пересечения биссектрис, то периметр 
NBM равен АВ+ВС.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Свойство катета прямоугольного треугольника, лежащего против угла в 30°
- Четырехугольник и его элементы
- Четырехугольники и окружность
- Параллелограмм, его свойства и признаки
- Признаки равенства прямоугольных треугольников
- Соотношения в прямоугольном треугольнике
- Сумма углов треугольника
- Внешний угол треугольника
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
💥 Видео
В треугольнике ABC известно, что угол BAC = 42 градуса, AD - биссектриса. Найдите угол BAD. Ответ даСкачать
№538. Биссектриса AD треугольника ABC делит сторону ВС на отрезки CD и BD, равные соответственноСкачать
№191. Отрезок ВК — биссектриса треугольника ABC. Через точку К проведена прямая, пересекающаяСкачать
🔴 В треугольнике ABC проведена биссектриса ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 15 | ШКОЛА ПИФАГОРАСкачать
№235. В равнобедренном треугольнике ABC с основанием АС проведена биссектриса AD. Найдите углыСкачать
Высота, биссектриса, медиана. 7 класс.Скачать
Геометрия Отрезок AD – биссектриса треугольника ABC. Через точку C проведена прямая, котораяСкачать
№536. Отрезок BD является биссектрисой треугольника ABC. а) Найдите АВ, если ВС = 9 смСкачать
ЕГЭ 1 задание ✧ В треугольнике ABC проведена биссектриса AD и AB = AD = CD. Найти меньший угол ∆ABCСкачать
№139. На рисунке 76 АВ = CD, AD = ВС, BE — биссектриса угла ABC, a DF — биссектриса угла ADC.Скачать
№537. Отрезок AD является биссектрисой треугольника ABC. Найдите BD и DC, если АВ = 14 смСкачать
Формула для биссектрисы треугольникаСкачать
Геометрия Отрезок AD биссектриса треугольника ABC Площадь треугольника ABD равна 12 см2Скачать
1780 В треугольнике ABC AD биссектриса угол C равен 30° угол BAD равен 69 Найдите угол ADBСкачать
№229. В равнобедренном треугольнике ABC с основанием АС проведена биссектриса AD.Скачать
Геометрия Отрезок CD биссектриса треугольника ABC Через точку D проведена прямая которая параллельнаСкачать
